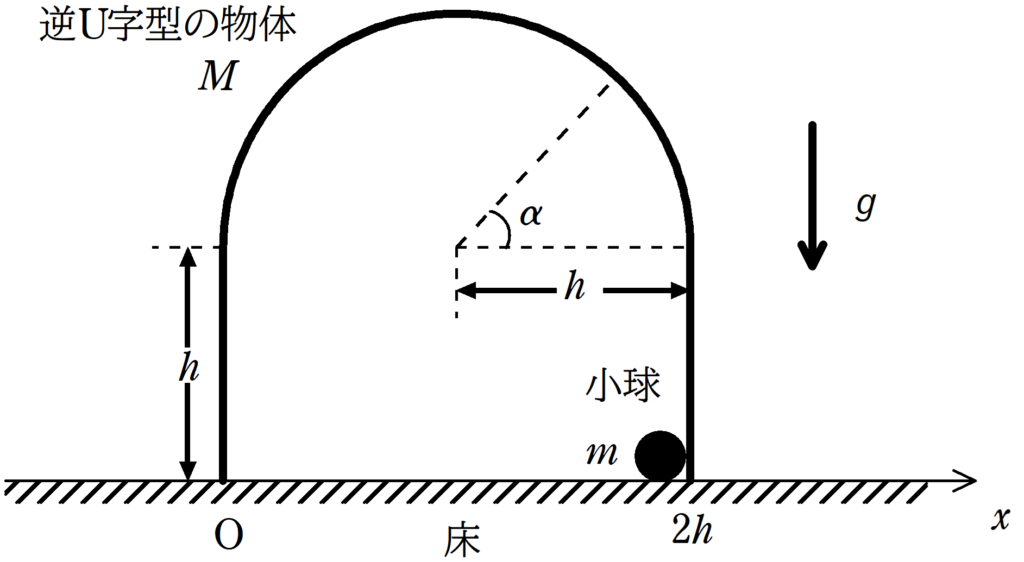
図のように,質量$M$の逆$\rm U$字型の物体が水平な床の上に置かれている.この物体は,鉛直に立つ高さ$h$の2枚の平板と,その上に接続された半径$h$の半円筒からなっている.図は真横から見た物体の断面,つまり平板と床に垂直な断面を示している.この物体は密度が一様な材質でできており,その厚さは無視できる.断面内における物体の左端を原点として,水平右向きを正とするように床上に$x$軸をとる.また,質量$m$の小球が,物体の内壁の右端$x=2h$の位置に置かれている.小球は断面内でのみ運動し,小球と物体の内壁との間に生じる摩擦は無視できる.鉛直下向きの重力加速度の大きさを$g$とする.
(1) 略
(2) 略
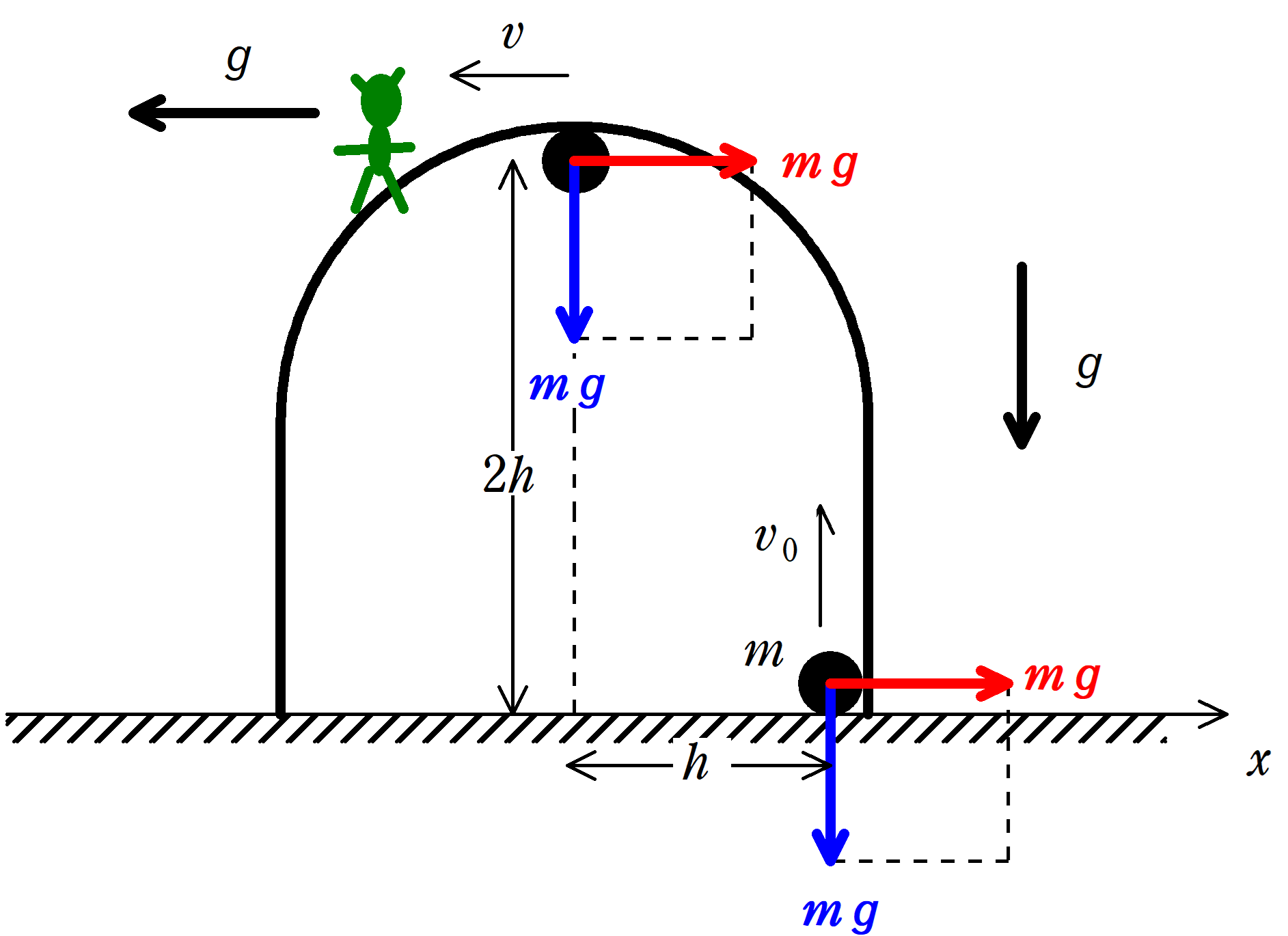
(3) 次に,逆$\rm U$字型の物体を,$x$軸の負の方向に大きさ$g$の等加速度で動かす場合を考える.ここで,$g$は重力加速度の大きさと同じである.物体とともに動く座標系で,小球を内壁の右端の床面から大きさ$v_{0}$の初速度で鉛直上向きに打ち上げた.この座標系で見ると,大きさが$\fbox{ (ク) }$の見かけの重力加速度が右下斜め$45°$方向に生じているとみなすことができる.小球は物体の内壁に沿って運動し,$\alpha=90°$の位置で内壁を離れた.このとき,見かけの重力加速度を使った力学的エネルギー保存の法則と,小球が内壁からうける垂直抗力が$0$になることを用いると,$v_{0}$は,$g$,$h$を用いて$v_{0}=\fbox{ (ケ) }$と書ける.
<解答>

(3)では,物体とともに動く座標系から小球の運動を観測します.
物体は,$x$軸の負の方向に加速度の大きさ$g$で等加速度運動しているので,物体から小球をみると,重力や物体からの垂直抗力のほかに慣性力がかかることに注意しましょう.
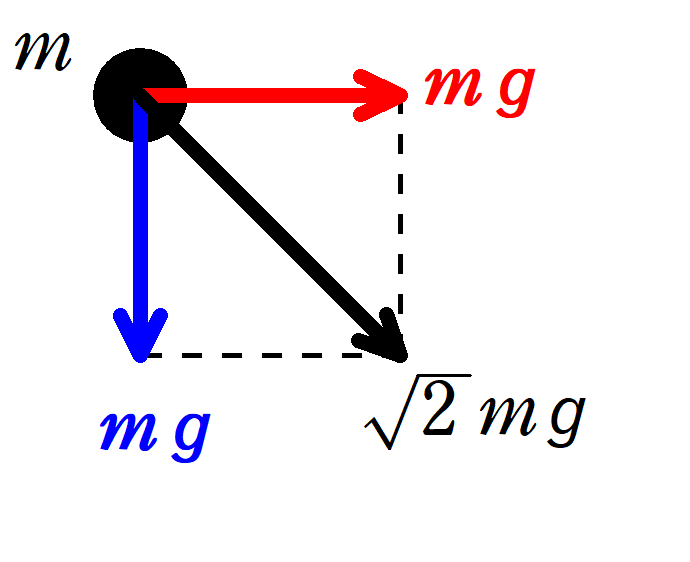

鉛直下向きに重力$mg$がはたらいて,$x$軸の正方向に慣性力$mg$がはたらくんだね.
その合力は$\sqrt{2}mg$なので,みかけの重力加速度の大きさは
$\fbox{ (ク) }\sqrt{2}g$ (答)

次に$\alpha=90°$のときの物体からみた小球の速さを求めるために,エネルギーの原理の式を立てます.
また,仕事の計算の仕方はこちらも参考にしてみてください.
質量$m$の物体の速さが$v_{0}$から$v$に変化したとき,この間に外力がした仕事を$W$とすると
$\dfrac{1}{2}mv^2-\dfrac{1}{2}mv_{0}^{2}=W$
の関係がある.
力×変位を仕事という.
しかし,等加速度運動の式から導いたことから,次のルールが加わる.
① 力は一定である.もし一定でないのであれば,一定とみなせるくらい細かく分解して足し合わせる(積分する.).
② 力の方向と移動する方向が一致する場合は正の仕事,反対方向の場合は負の仕事である.
③ 力の方向と移動する方向が一直線上にない場合は,仕事の大きさについて次のどちらかで計算をする.
- 力×力の方向に移動した距離 で計算.
- 力を移動する方向に分解して計算
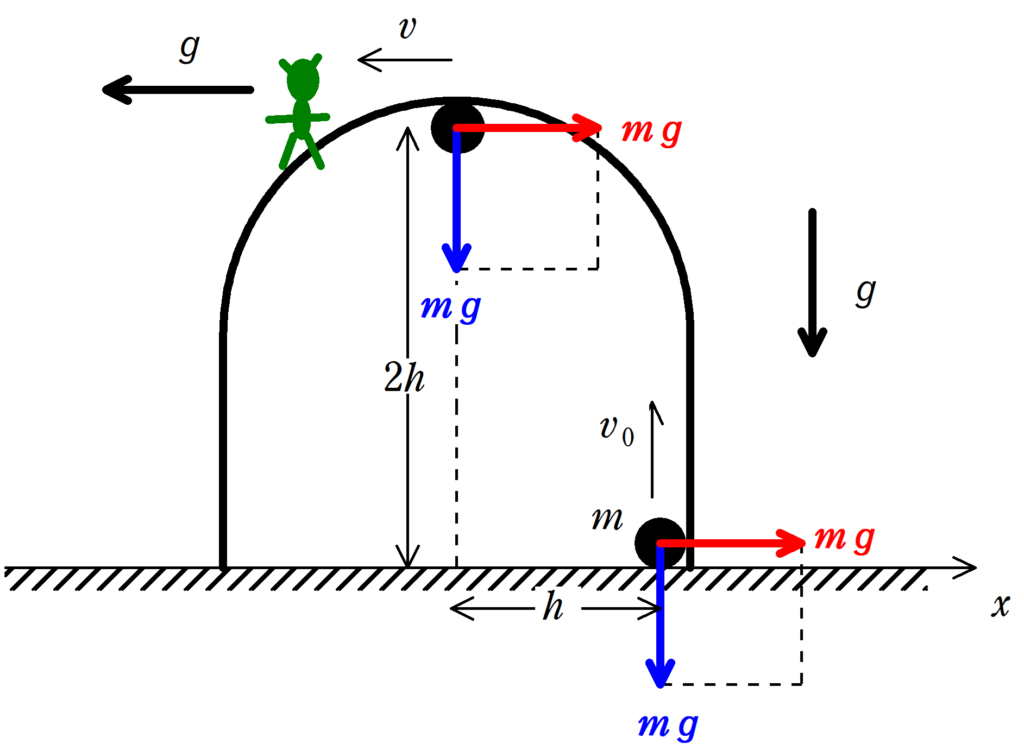

$\alpha=90°$のときの物体からみた小球の速さを$v$とおきましょう.
重力がする仕事$W_{1}$と慣性力がする仕事$W_{2}$はそれぞれ次のようになります.
★ 重力と慣性力がする仕事
$W_{1}=(-mg)\cdot 2h=-2mgh$
$W_{2}=(-mg)\cdot h=-mgh$

じゃあ,エネルギーの原理の式は次のようになるんだね.
★ エネルギーの原理の式
$\eqalign{\dfrac{1}{2}mv^{2}-\dfrac{1}{2}mv_{0}^{2}&=-2mgh-mgh\cr v^{2}&=v_{0}^{2}-6gh \dots (\ast)}$

速さがわかったら,$\alpha=90°$における向心方向の運動方程式を立てましょう.(円運動の運動方程式)
問題文に与えられているように,垂直抗力$N$は$0$なので,向心力は重力$mg$のみです.
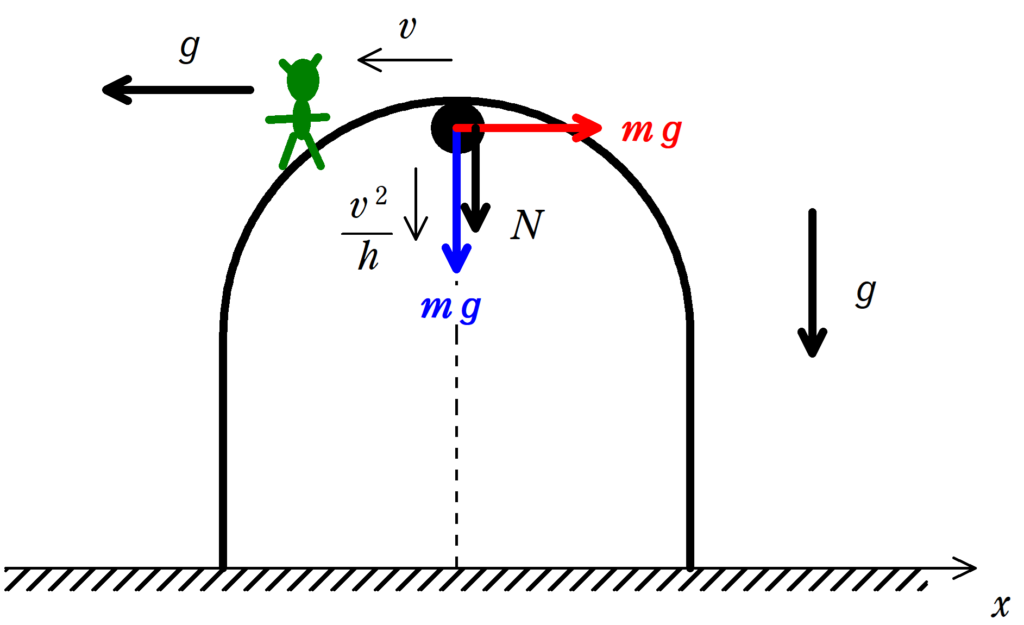
★ 向心方向の運動方程式
$m\dfrac{v^{2}}{h}=mg$
$\therefore v^{2}=gh$
$(\ast)$の$v^{2}=v_{0}^{2}-6gh$を代入して
$v_{0}^{2}-6gh=gh$
$\therefore v_{0}=\sqrt{7gh}$
したがって,$\fbox{ (ケ) }\sqrt{7gh}$ (答)



コメント
[…] […]