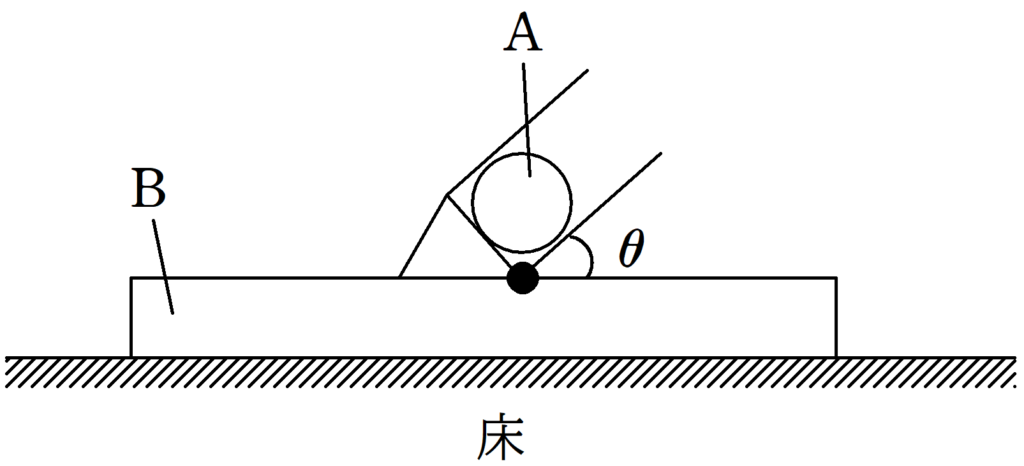
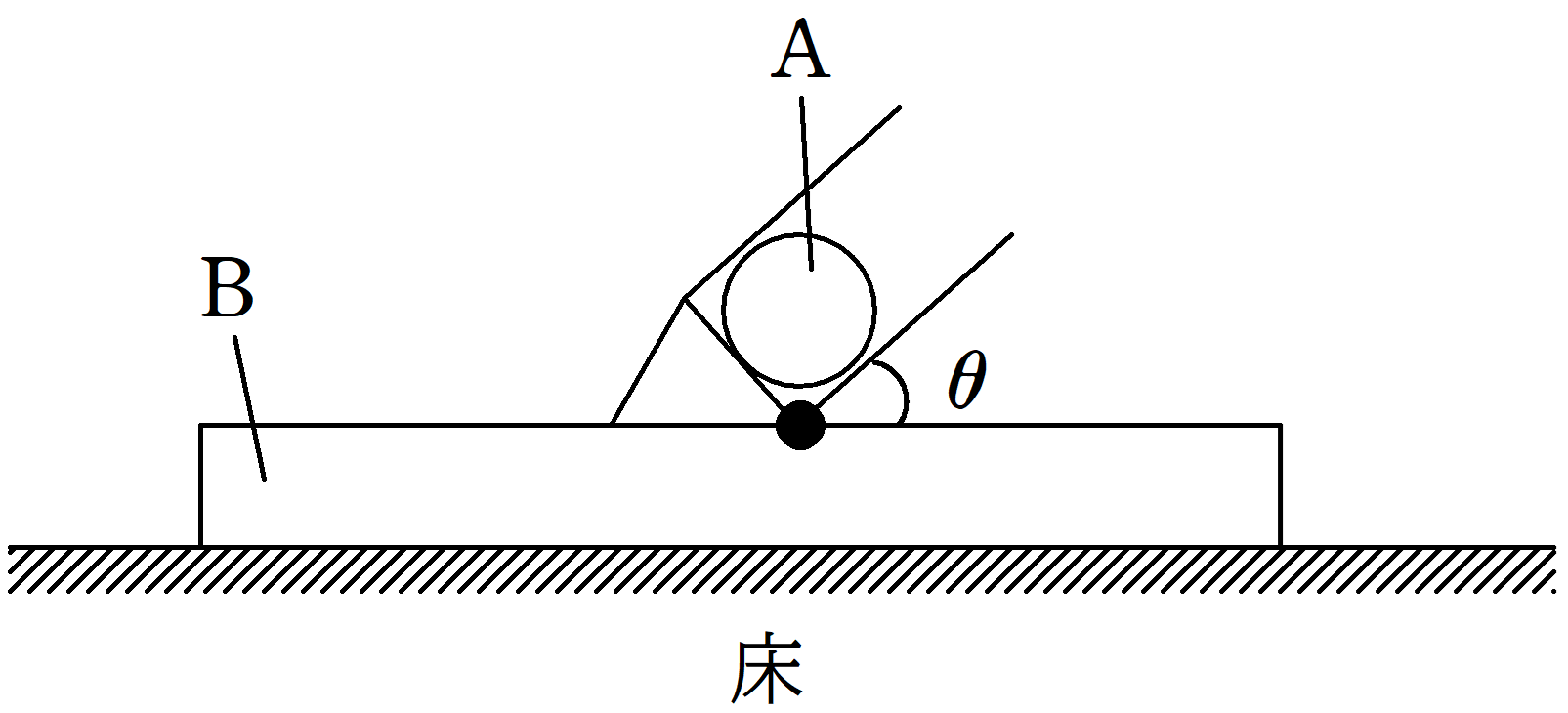
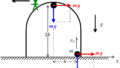
図のように,なめらかな水平面上に台車Bが置かれている.
Bには,質量$m$の小物体Aを発射できる発射装置が取り付けられている.
Aを除いた発射装置と台車の質量の合計は$M$であり,発射装置は台車の水平な上面となす角$\theta=45°$の方向に発射できるようにしてある.
発射装置が供給するエネルギーは$E(>0)$であり,エネルギー$E$はすべて小球と台車および発射装置の運動エネルギーに変わる.
台車は鉛直方向には運動をしないものとする.このとき,Aを発射直後の台車の速さを$m$,$M$,$E$を用いて表せ.
<解答>

水平方向の運動量保存則とエネルギー保存則を立てるために,発射直後の小球の速度を$(v_{x},v_{y})$,台車の速度を$(V, 0)$と設定します.
しかし,$\theta=45°$だからといって,小球の速度を$(v , v)$などと設定してはいけません.
なぜならば,静止した人から見た小球の速度と,Bの上から見た小球の速度は異なるからです.
速度が異なるということは,水平成分と鉛直成分の比も異なります.
実際,$\theta$はBの上から速度の方向であって,静止した人から速度の方向ではありません.
こちらの記事でも確認してください.
観測者によって速度の大きさや向きは異なって見える.
したがって,物体の進む向きも観測者によって異なる.
物体の進む方向が問われたとき,誰から見た方向を聞かれているのかを確認すること.
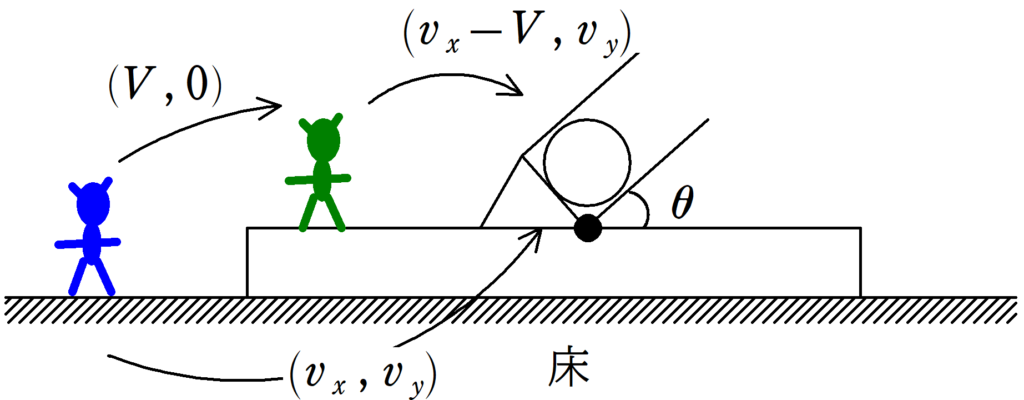

いまいちど,問題設定をしましょう.
静止した人から見た(青い人)小球の速度を$(v_{x},v_{y})$,台車の速度を$(V, 0)$とします.
すると,台車からみた(緑の人)小球の速度は$(v_{x}-V , v_{y})$となります.
台車からみた小球の水平成分と鉛直成分の大きさは$\theta=45°$であることから,$1:1$となります.
すなわち
★ $v_{x}$,$V$,$v_{y}$の関係
$\dfrac{v_{y}}{v_{x}-V}=1$
$\therefore v_{y}=v_{x}-V$ $\dots (\ast)$

さらに,運動量保存則とエネルギー保存則を立てます.
★ 水平方向の運動量保存則
$0=mv_{x}+MV$ $\dots (2\ast)$
★ エネルギー保存則
$E=\dfrac{1}{2}m(v_{x}^{2}+v_{y}^{2})+\dfrac{1}{2}MV^{2}$ $\dots (3\ast)$

$(\ast)$~$(3\ast)$の式より,$V$を求めましょう.
$(2\ast)$より
$v_{x}=-\dfrac{M}{m}V$ $\dots (4\ast)$
$(4\ast)$を$(\ast)$に代入すると
$\eqalign{v_{y}&=v_{x}-V\\&=-\dfrac{M}{m}V-V\\&=-\dfrac{M+m}{m}V \dots (5\ast)} $
$(4\ast)$,$(5\ast)$を$(3\ast)$に代入する
$\eqalign{E&=\dfrac{1}{2}m\left(\dfrac{M^{2}}{m^{2}}V^{2}+\dfrac{(M+m)^{2}}{m^{2}}V^{2}\right)+\dfrac{1}{2}MV^{2}\cr \dfrac{1}{2}\cdot \dfrac{2M^{2}+3Mm+m^{2}}{m}V^{2}&=E\cr \dfrac{1}{2}\dfrac{(2M+m)(M+m)}{m}V^{2}&=E\cr V^{2}&=\dfrac{2mE}{(2M+m)(M+m)}}$
したがって,台車の速さは,$|V|=\sqrt{\dfrac{2mE}{(2M+m)(M+m)}}$(答)



コメント