[2021慶應理工1（2）の(エ)(オ)]角度に注意

2021　慶應義塾大　理工　1.(2)の(エ)と(オ)

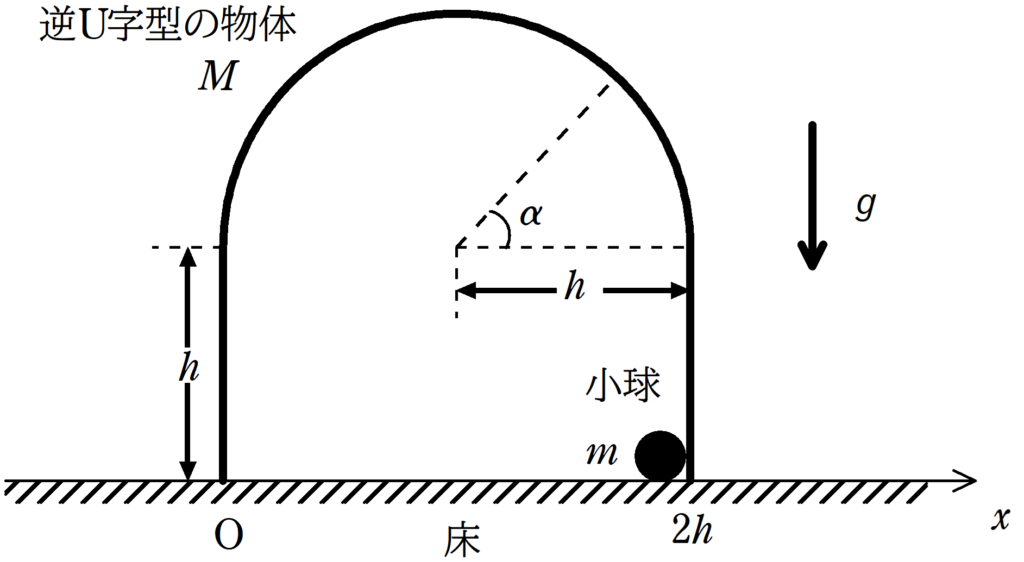
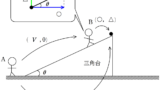
図のように，質量$M$の逆$\rm U$字型の物体が水平な床の上に置かれている．この物体は，鉛直に立つ高さ$h$の2枚の平板と，その上に接続された半径$h$の半円筒からなっている．図は真横から見た物体の断面，つまり平板と床に垂直な断面を示している．この物体は密度が一様な材質でできており，その厚さは無視できる．断面内における物体の左端を原点として，水平右向きを正とするように床上に$x$軸をとる．また，質量$m$の小球が，物体の内壁の右端$x=2h$の位置に置かれている．小球は断面内でのみ運動し，小球と物体の内壁との間に生じる摩擦は無視できる．鉛直下向きの重力加速度の大きさを$g$とする．

(1)　略

(2)　次に，逆$\rm U$字型の物体を床に固定せずに，床の上でなめらかに動ける状態にした．小球を内壁の右端の床面から大きさ$v_{0}$の初速度で鉛直上向きに打ち上げると，小球は物体の内壁に沿って半円筒の領域に入り，物体は小球から力を受けて水平方向に床を離れずに運動した．水平方向には外力がはたらいていないことから，角度$\alpha$の位置における小球の速度の大きさを$v_{\alpha}$とすると，逆$\rm U$字型の物体の速度は，$m$，$M$，$\alpha$，$v_{\alpha}$を用いて$\fbox{ (エ) }$と書ける．さらに，力学的エネルギー保存の法則から，小球の速度の大きさ$v_{\alpha}$は，$m$，$M$，$g$，$h$，$\alpha$，$v_{0}$を用いて$v_{\alpha}=\fbox{ (オ) }$と書ける．（以後省略）

<解答>

PHYさん

今回は，2021年慶應義塾大の理工の第1問のやや取りくみにくい運動量保存則と力学的エネルギー保存則を立てる(エ)と(オ)のみを扱います．

今回の間違いやすいポイントは

「角度$\alpha$の位置において，床で静止した人からみたときの小物体の水平方向の速度は$-v_{\alpha}\sin\alpha$ではない．」

というところです．

つまり，$v_{\alpha}$を次のように分解してはだめです．

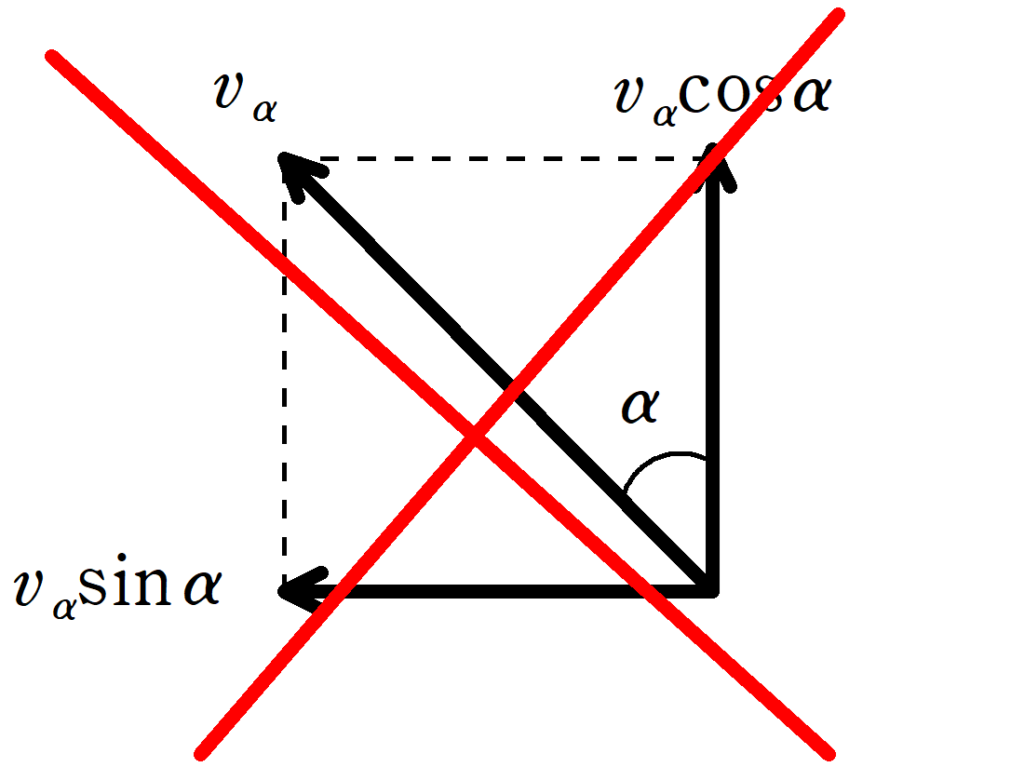
このような，角度の間違いは過去にもいろいろな問題で出ています．

このブログでも次の記事で扱っています．

[よくある間違い]動く斜面から飛び出す物体の軌道のなす角

NEKO 今回は，よくある間違いシリーズです． 次の問題をみてみましょう 問題 なめらかな水平面の上に傾角$\theta$の斜面をもつ三角台がおかれていて，水平方向に自由に動くことができる． 水平面にある小物体に初速を与えたところ，小物体は...

physicmath.net

2020.11.22

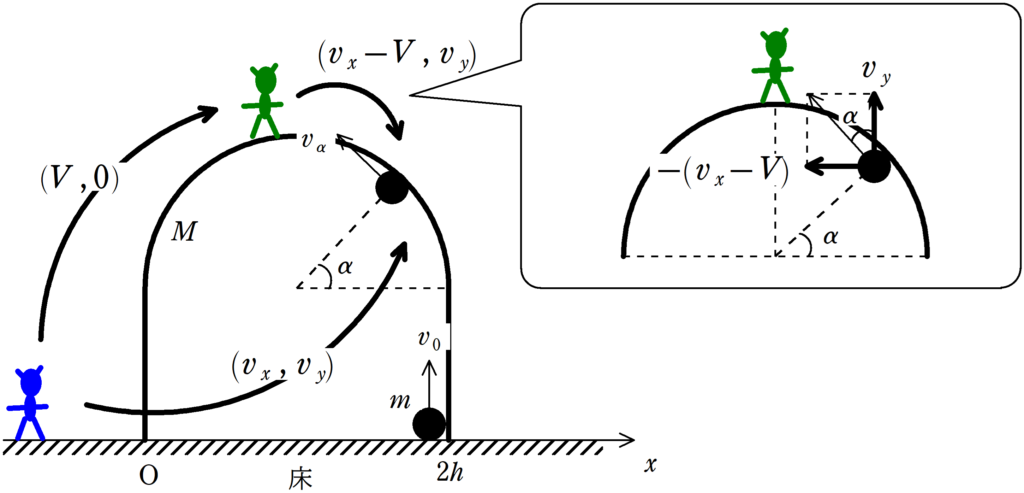
●　設定

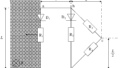
小物体が角度$\alpha$の位置にきたときの$\rm U$字型の物体の速度を$(V , 0)$，小物体の速度を$(v_{x},v_{y})$とします．（水平右向き，鉛直上向きをそれぞれ正とする．）

すると，$\rm U$字型の物体からみた小物体の速度（上図の緑の人からみた速度）は$(v_{x}-V ,v_{y})$となります．

PHYさん

まず，$\alpha\neq 90°$（すなわち，$v_{y}\neq 0$）のときから考えましょう．

このとき，$\rm U$字型の物体からみた（緑の人からみる）小物体の速さの比を考えると，次のようになります．

$\tan\alpha=\dfrac{-(v_{x}-V)}{v_{y}}$　$\dots (\ast)$

さらに，運動量保存則と力学的エネルギー保存則を立てましょう．

運動量保存則は水平方向の速度成分のみです．なので，小物体の速度は$v_{x}$を用います．

また，運動量保存則は基本的に静止している観測者から立ててください．

★　水平方向の運動量保存則

$0=mv_{x}+MV$　$\dots　(2\ast)$

★　力学的エネルギー保存則

$\dfrac{1}{2}mv_{0}^{2}=\dfrac{1}{2}mv_{\alpha}^{2}+\dfrac{1}{2}MV^{2}+mgh(1+\sin\alpha)$　$\dots　(3\ast)$

★　$v_{\alpha}$と$v_{x}$と$v_{y}$の関係

$v_{\alpha}^{2}=v_{x}^{2}+v_{y}^{2}$　$\dots　(4\ast)$

NEKO

あとは，これを解くだけだね．

まず，$\fbox{ (エ) }$では，速度$V$を問われているので，$v_{x}$や$v_{y}$を消去しましょう．

$(2\ast)$の$0=mv_{x}+MV$より

$v_{x}=-\dfrac{M}{m}V$　$\dots　(5\ast)$

さらに，$(\ast)$の$\tan\alpha=\dfrac{-(v_{x}-V)}{v_{y}}$より

$\eqalign{v_{y}&=-\dfrac{v_{x}-V}{\tan\alpha}\\&=-\dfrac{1}{\tan\alpha}\left(-\dfrac{M}{m}V-V\right)\\&=\dfrac{1}{\tan\alpha}\cdot\dfrac{M+m}{m}V \dots (6\ast)}$

NEKO

上式では，途中$(5\ast)$の$v_{x}=-\dfrac{M}{m}V$を代入しました．

さらに，$(4\ast)$の$v_{\alpha}^{2}=v_{x}^{2}+v_{y}^{2}$に$(5\ast)$の$v_{x}=-\dfrac{M}{m}V$と$(6\ast)$の$v_{y}=\dfrac{1}{\tan\alpha}\cdot\dfrac{M+m}{m}V$を代入して，

$\eqalign{v_{\alpha}^{2}&=\left(-\dfrac{M}{m}V\right)^{2}+\left(\dfrac{1}{\tan\alpha}\cdot\dfrac{M+m}{m}V\right)^{2}\cr V&=\dfrac{m\tan\alpha}{\sqrt{M^{2}\tan^{2}\alpha +(M+m)^{2}}}v_{\alpha}}$

PHYさん

このままでは，$\alpha=90°$ときに使えない式になってしまうので，分子分母に$\cos\alpha$をかけて，$\tan$をなくしましょう．

$\therefore　V=\dfrac{m\sin\alpha}{\sqrt{M^{2}\sin^{2}\alpha +(M+m)^{2}\cos^{2}\alpha }}v_{\alpha}$　($\fbox{ (エ) }$の答)

PHYさん

しかし，これは$\alpha=90°$のときは除いています．

$\alpha=90°$のとき，上式は

$V=\dfrac{m}{M}v_{\alpha}$

です．

実際，$\alpha=90°$のときは，$v_{x}=-v_{\alpha}$です．

運動量保存則より，

$0=m(-v_{\alpha})+MV$

なので，$V=\dfrac{m}{M}v_{\alpha}$となり，答えの式を満たしています．したがって，$0°<\alpha<180°$のすべての角度で答えの式が成り立ちます．

NEKO

最後に，(エ)で得た式

$V=\dfrac{m\sin\alpha}{\sqrt{M^{2}\sin^{2}\alpha +(M+m)^{2}\cos^{2}\alpha }}v_{\alpha}$

を$(3\ast)$の式

$\dfrac{1}{2}mv_{0}^{2}=\dfrac{1}{2}mv_{\alpha}^{2}+\dfrac{1}{2}MV^{2}+mgh(1+\sin\alpha)$

に代入して$v_{\alpha}$について解きます．

$\eqalign{mv_{\alpha}^{2}+MV^{2}&=mv_{0}^{2}-2mgh(1+\sin\alpha)\cr mv_{\alpha}^{2}+\dfrac{Mm^{2}\sin^{2}\alpha}{M^{2}\sin^{2}\alpha +(M+m)^{2}\cos^{2}\alpha}v_{\alpha}^{2}&=mv_{0}^{2}-2mgh(1+\sin\alpha)\cr \dfrac{M^{2}\sin^{2}\alpha +(M+m)^{2}\cos^{2}\alpha +Mm\sin^{2}\alpha}{M^{2}\sin^{2}\alpha +(M+m)^{2}\cos^{2}\alpha}v_{\alpha}^{2}&=v_{0}^{2}-2gh(1+\sin\alpha)\cr \dfrac{(M+m)(M+m\cos^{2}\alpha)}{M^{2}\sin^{2}\alpha +(M+m)^{2}\cos^{2}\alpha}v_{\alpha}^{2}&=v_{0}^{2}-2gh(1+\sin\alpha)\cr v_{\alpha}&=\sqrt{\dfrac{M^{2}\sin^{2}\alpha +(M+m)^{2}\cos^{2}\alpha}{(M+m)(M+m\cos^{2}\alpha)}\left\{v_{0}^{2}-2gh(1+\sin\alpha)\right\}}}$

したがって，$\fbox{ (オ) }$　$\sqrt{\dfrac{M^{2}\sin^{2}\alpha +(M+m)^{2}\cos^{2}\alpha}{(M+m)(M+m\cos^{2}\alpha)}\left\{v_{0}^{2}-2gh(1+\sin\alpha)\right\}}$ (答)