
波の干渉条件を考えるとき,波長を$\lambda$,$m$を整数とすると,次が成り立つよね.
距離の差$=m\lambda$ $\dots$ 強め合いの条件
距離の差$=(m+\dfrac{1}{2})\lambda$ $\dots$ 弱め合いの条件
けど,少し条件が変わると,強め合いの条件と弱め合いの条件が逆になって混乱するんだよね.

そうですね.
固定端反射したり,はじめの位相が逆だったりすることで形は変わりますね.
実は,”距離の差=〇”の形よりも”位相差=〇”の式の方が波の干渉を統一的に考えることができるんです.
今回は,位相差$\phi$を使った条件を考えてみましょう.
★ メリット
・強め合いの条件,弱め合いの条件を1つ覚えればよいので,混乱しない.
・位相がずれるポイントを確認する癖がつく.
★ デメリット
・慣れていないと,計算が複雑に見えてしまう.

位相に関する記事はこちらにあるので,読んでみてね.
位相差による強め合いの条件と弱め合いの条件

まずは,位相差による強め合いの条件と弱め合いの条件についてまとめましょう.
地点Pにおける2つの波の位相差を$\phi$,整数を$m$とすると,
強め合いの条件:$\phi=2\pi m$
弱め合いの条件:$\phi=(2m+1)\pi $

位相差が$0 , 2\pi , 4\pi ,\dots$なら同じタイミングで振動するから強め合い,位相差が$\pi , 3\pi , 5\pi , \dots$なら真逆のタイミングで振動するから弱め合いってことだね.
位相差が生じる3つの要素

次に,位相差が生じる原因について考えましょう.
位相差が生じる原因は次の3つがあります.
位相差$\phi$は主に次の3つの位相差によって決まる.
$\phi_{1}$:初期位相のずれ
$\phi_{2}$:反射による位相のずれ
$\phi_{3}$:距離の差(屈折率が変わることで生じる光学的な距離の差を含む)による位相のずれ
このとき,位相差$\phi$は
$\phi=\phi_{1}+\phi_{2}+\phi_{3}$

なるほど!
干渉問題を考える際は,この3つの要素を考えればいいわけだね!
初期位相による位相のずれ

まずは初期位相です.
水面波の干渉問題でよくありますね.
下図のように,
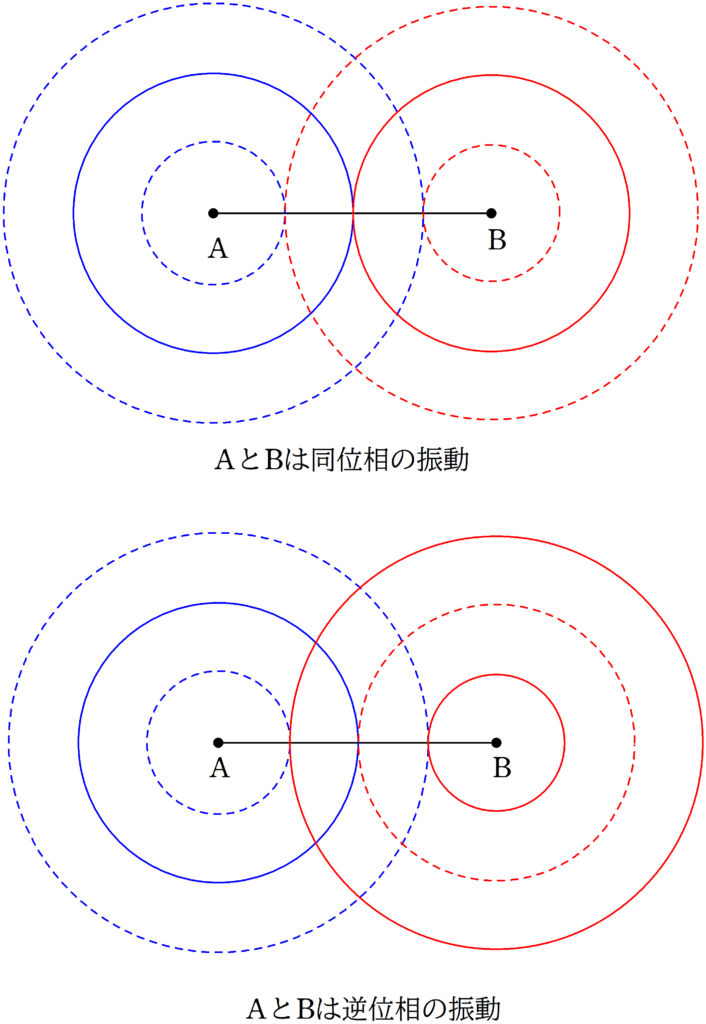
AとBが同位相で振動しているもの
と
AとBが逆位相で振動しているもの
で干渉条件は違います.
AとBが同位相で振動してれば,初期位相の差は$\phi_{1}=0$,AとBが逆位相で振動していれば,初期位相の差は$\phi_{1}=\pi$となります.
反射による位相のずれ

固定端反射すると位相が$\pi$ずれるんだよね.
こちらでも解説しているよ.

固定端反射は,問題文に書かれていることもありますが,光の干渉のときは屈折率の大小で自由端反射なのか,固定端反射なのかを読み取る必要があります.
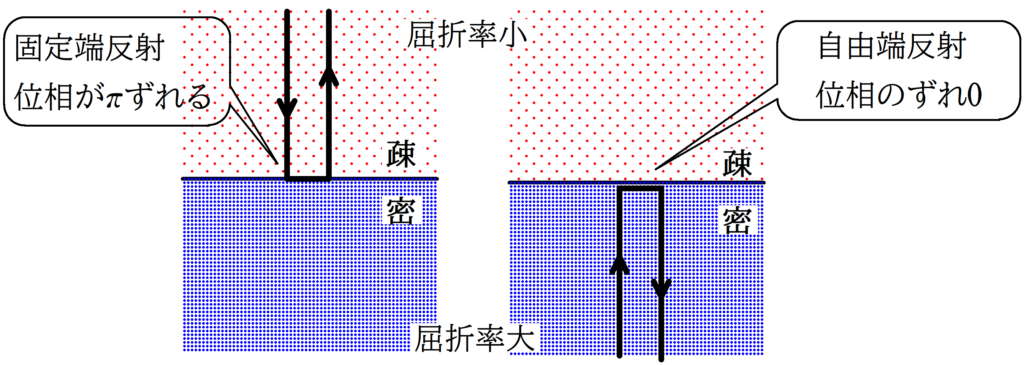

屈折率が小さい方から大きい方へ反射する場合は固定端反射で,位相が$\pi$ずれて,屈折率が大きい方から小さい方へ反射する場合は自由端反射で,位相のずれはないんだよね.
距離の差による位相のずれ

たとえ,初期位相が同じであっても距離の差があると,振動のタイミングがずれてしまいます.
下図ではAから出てくる波とBから出てくる波のPにおける干渉を考える際,距離の差は$\Delta l=l_{\rm{A}}-l_{\rm{B}}$となっています.
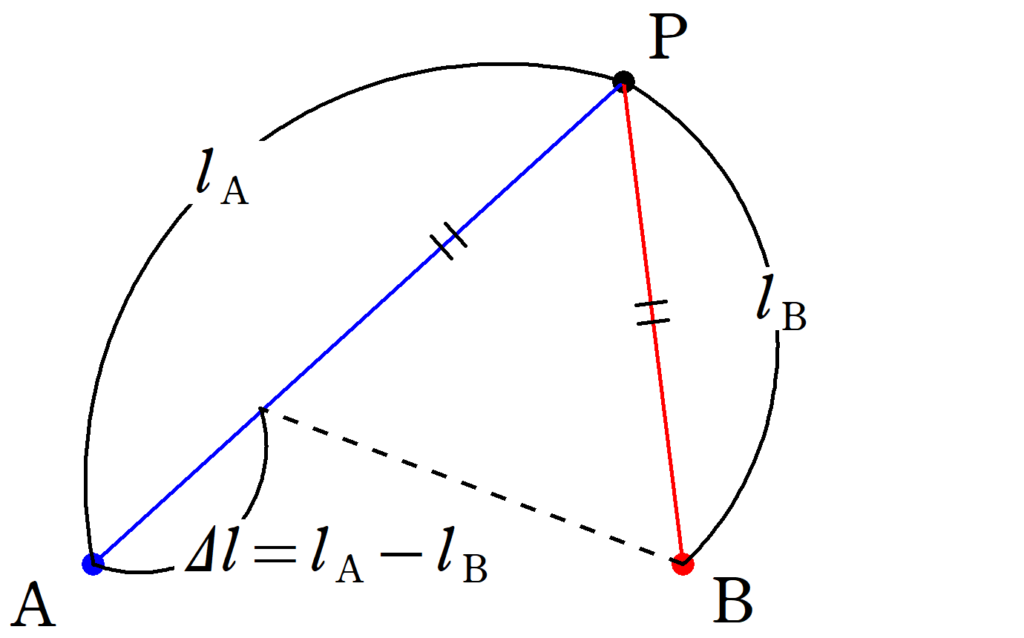

距離の差による位相のずれはどうやって計算すればいいの?

比例関係を使えば簡単に計算できます.
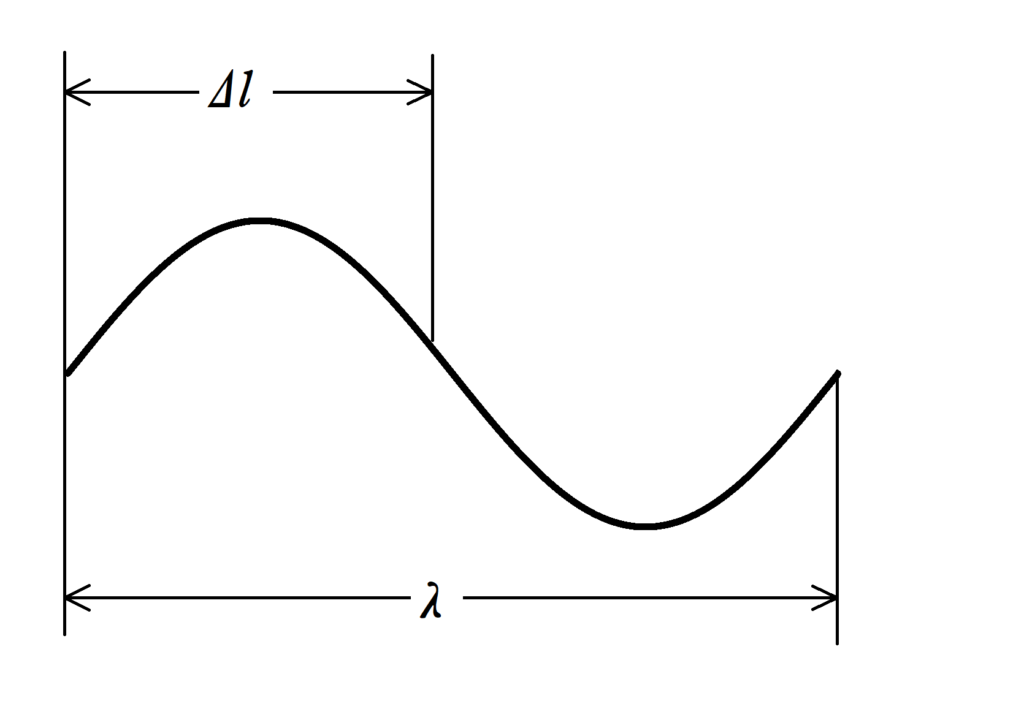
波1個分の長さである波長$\lambda$は位相$2\pi$に相当します.
なので,長さ$\Delta l$に相当する位相差$\phi_{3}$は比例式を立てて
$2\pi : \lambda =\phi_{3} : \Delta l$
$\therefore \phi_{3}=\dfrac{2\pi}{\lambda}\Delta l$
となります.
まとめ
地点Pにおける2つの波の位相差を$\phi$,整数を$m$とすると,
強め合いの条件:$\phi=2\pi m$
弱め合いの条件:$\phi=(2m+1)\pi $
位相差$\phi$は次の3つの要素で決まる.
$\phi_{1}$:初期位相のずれ
同位相なら$\phi_{1}=0$,逆位相なら$\phi_{1}=\pi$
$\phi_{2}$:反射による位相のずれ
自由端反射なら$\phi_{2}=0$,固定端反射なら$\phi_{2}=\pi$
$\phi_{3}$:距離の差(屈折率が変わることで生じる光学的な距離の差を含む)による位相のずれ
距離の差が$\Delta l$のとき,次の比例式を立てて,位相差$\phi_{3}$を計算する.
$2\pi : \lambda =\phi_{3} : \Delta l$
$\therefore \phi_{3}=\dfrac{2\pi}{\lambda}\Delta l$
このとき,位相差$\phi$は
$\phi=\phi_{1}+\phi_{2}+\phi_{3}$
演習問題

最後に演習問題を解いて確認しよう!
以下,答えに整数$m$を用いてよい.
[A]
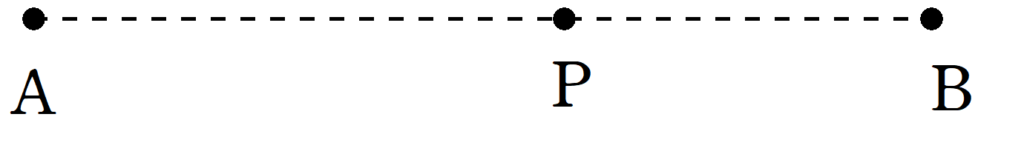
(1) AとBが同位相で振動している.$\rm{AP-BP}$$=\Delta l$であるとき,Pにおける強め合いの条件と弱め合いの条件をかけ.ただし,波長を$\lambda$とする.
(2) AとBが逆位相で振動している.$\rm{AP-BP}$$=\Delta l$であるとき,Pにおける強め合いの条件と弱め合いの条件をかけ.ただし,波長を$\lambda$とする.
[B]
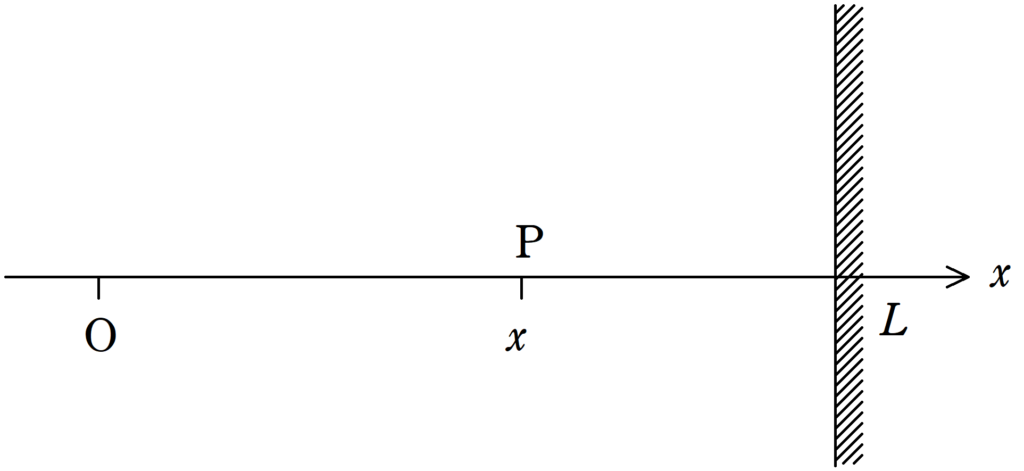
図のように,原点Oより$x$軸の正の方向に波が伝わっている.波は$x=L$で固定端反射され,その後$x$軸の負の向きに進む.このとき,Oから直接P(座標$x$)に伝わる波とOから伝わる波が固定端反射してPに伝わる波の強め合いの条件と弱め合いの条件をかけ.たたし,波長を$\lambda$とする.
<解答>
[A]
(1) 初期位相のずれ,反射によるずれはないので,距離の差による位相のずれ$\phi_{3}$を考えればよいです.比例式を立てて
$2\pi : \lambda =\phi_{3} : \Delta l$ $\therefore \phi_{3}=\dfrac{2\pi}{\lambda}\Delta l$
したがって,強め合いの条件は
$\phi_{3}=2\pi m$
$\dfrac{2\pi}{\lambda}\Delta l=2\pi m$ (答)
ちなみに,次のように変形すると,いつもの強め合いの条件になります.
$\Delta l=m\lambda$
弱め合いの条件は
$\phi_{3}=(2m+1)\pi$
$\dfrac{2\pi}{\lambda}\Delta l=(2m+1)\pi$ (答)
こちらも,次のように変形できます.
$\Delta l=(m+\dfrac{1}{2})\lambda$
(2) 初期位相の差が$\phi_{1}=\pi$なので,(1)の距離の差による位相のずれも考慮して,強め合いの条件は
$\eqalign{\phi_{1}+\phi_{3}&=2\pi m \cr \dfrac{2\pi}{\lambda}\Delta l &=(2m-1)\pi}$ (答)
変形すると
$\Delta l=(m-\dfrac{1}{2})\lambda$
となります.
弱め合いの条件は
$\eqalign{\phi_{1}+\phi_{3}&=(2m+1)\pi \cr \dfrac{2\pi}{\lambda}\Delta l &=2m\pi}$ (答)
変形すると
$\Delta l=m\lambda$
となります.
[B]
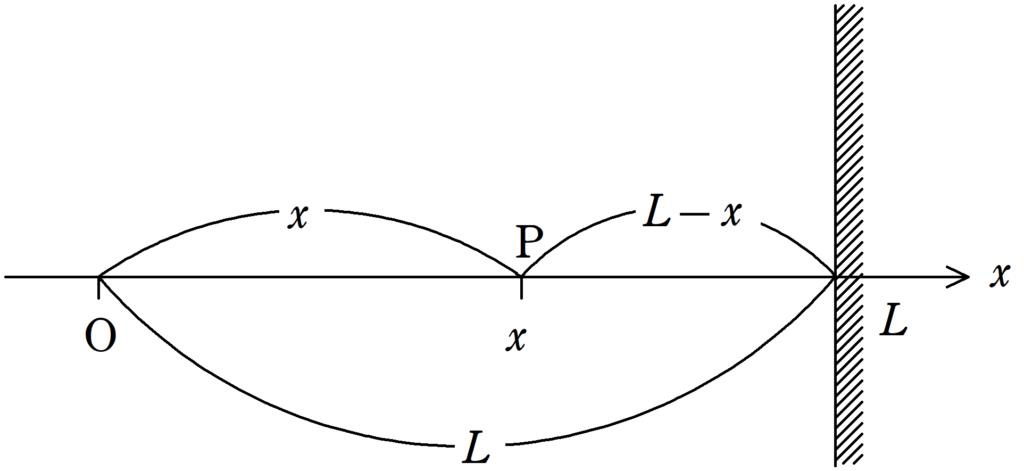
O→PもO→反射→Pも出発点はどちらもOなので,初期位相のずれは0です.
一方,O→反射→Pの方は固定端反射するので,位相のずれは$\phi_{2}=\pi$となります.
最後に距離の差による位相のずれです.
O→反射→Pの経路の長さは$L+(L-x)=2L-x$,O→Pの経路の長さは$x$なので,経路差$\Delta l$は
$\Delta l=(2L-x)-x=2(L-x)$
となります.したがって,距離の差による位相のずれ$\phi_{3}$は
$2\pi : \lambda =\phi_{3} : 2(L-x)$
$\phi_{3}=\dfrac{2\pi}{\lambda}\cdot 2(L-x)$
となります.以上より,強め合いの条件は
$\eqalign{\phi_{2}+\phi_{3}&=2\pi m \cr \pi +\dfrac{2\pi}{\lambda}\cdot 2(L-x)&=2\pi m \cr \dfrac{2\pi}{\lambda}\cdot 2(L-x)&=(2m-1)\pi }$ (答)
また,変形すると
$2(L-x)=(m-\dfrac{1}{2})\lambda$
同じく,弱め合いの条件は
$\eqalign{\phi_{2}+\phi_{3}&=(2m+1)\pi \cr \pi +\dfrac{2\pi}{\lambda}\cdot 2(L-x)&=(2m+1)\pi \cr \dfrac{2\pi}{\lambda}\cdot 2(L-x)&=2m\pi }$ (答)
また,変形すると
$2(L-x)=m\lambda$

もれなく位相がずれるポイントを考えよう.





コメント
[…] 位相差のススメ[波の干渉]NEKO波の干渉条件を考えるとき,波長を$lambda$,$… PHYさん […]
[…] 位相差のススメ[波の干渉] […]
[…] ・「位相差による条件」がよくわからない人は「位相差のススメ」 […]