波の式と干渉1 | Physicmath（フィジクマス）

問題

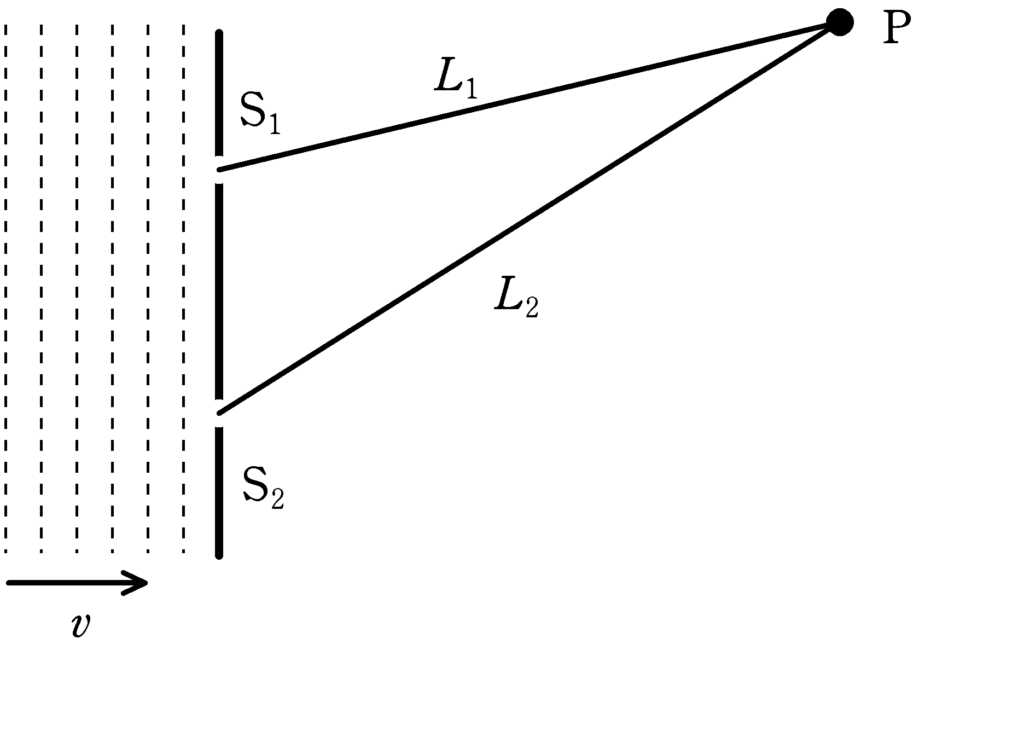
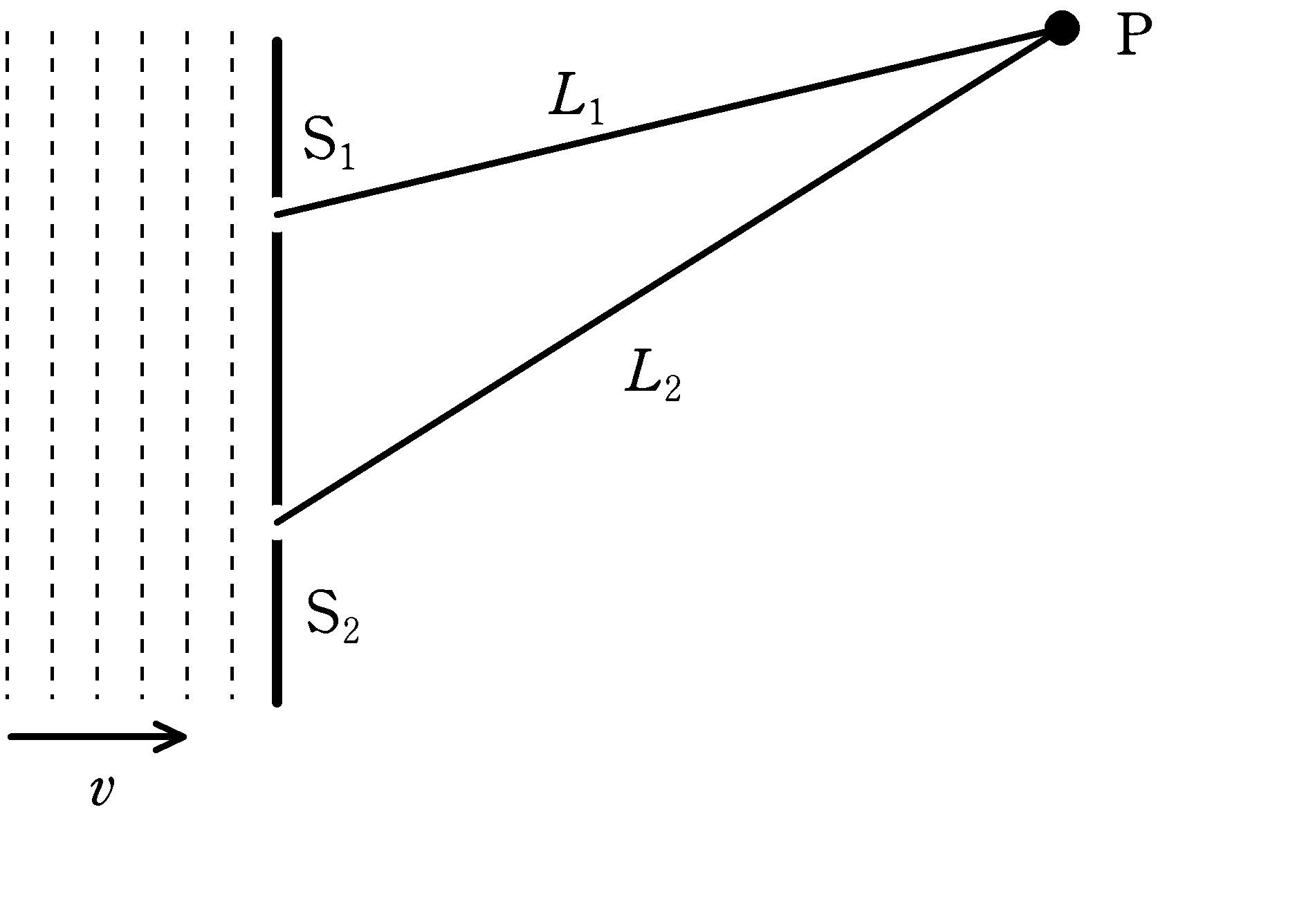
スリット$\rm S_{1}$，$\rm S_{2}$をもつ薄い板に波長$\lambda$の平面波を波面と板の面が平行になるようにあてる．平面波は$\rm S_{1}$，$\rm S_{2}$で回折した．ただし，波長は回折前と回折後で変化はなく，$\rm S_{1}$，$\rm S_{2}$における時刻$t$媒質の変位$y$は，振幅を$A\,(>0)$，周期$T$を用いて，ともに

$y=A\sin\dfrac{2\pi}{T}t$

である．図の$\rm S_{1}$からPまでの距離を$L_{1}$，$\rm S_{2}$からPまでの距離を$L_{2}$とする．次の問いに答えよ．

(1)　時刻$t$において，$\rm S_{1}$からPに伝わった波の変位を$y_{1}$，$\rm S_{2}$からPに伝わった波の変位を$y_{2}$とする．$y_{1}$，$y_{2}$を，$A，T，v，L_{1}，L_{2}，t$から必要なものを用いて表せ．

(2)　時刻$t$におけるPの変位は$y=y_{1}+y_{2}$である．この合成波の振幅を$A，L_{1}，L_{2}，v，T$を用いて表せ．

(3)　Pの波の変位が時刻によらず常に0であった．このとき，$L_{2}-L_{1}$を整数$m$と波長$\lambda$を用いて表せ．

<解答>

(1)

PHYさん

波の式については，こちらでも扱っています．

ぜひご覧ください．

★　$y_{1}$について

($\rm S_{1}$から伝わる)Pの波の変位は時間$\dfrac{L_{1}}{v}$前の$\rm S_{1}$の波の変位と等しいから

$y_{1}=A\sin\left\{\dfrac{2\pi}{T}\left(t-\dfrac{L_{1}}{v}\right)\right\}$　(答)

★　$y_{2}$について

($\rm S_{2}$から伝わる)Pの波の変位は時間$\dfrac{L_{2}}{v}$前の$\rm S_{2}$の波の変位と等しいから

$y_{2}=A\sin\left\{\dfrac{2\pi}{T}\left(t-\dfrac{L_{2}}{v}\right)\right\}$　(答)

(2)　

PHYさん

三角関数の和→積の変換式を用いて振幅を求めます．

$\eqalign{y&=y_{1}+y_{2}\\&= A\sin\left\{\dfrac{2\pi}{T}\left(t-\dfrac{L_{1}}{v}\right)\right\} + A\sin\left\{\dfrac{2\pi}{T}\left(t-\dfrac{L_{2}}{v}\right)\right\} \cdots (\sharp)}$

和から積への変換

まず，正弦の加法定理を書き出します．

$\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta$　$\cdots (\ast)$

$\sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta$　$\cdots (2\ast)$

$(\ast)+(2\ast)$を計算します．

$\sin(\alpha+\beta)+\sin(\alpha-\beta)=2\sin\alpha\cos\beta$　$\cdots (\clubsuit)$

この式と$(\sharp)$との対応関係を書き出しましょう．

$\alpha+\beta= \dfrac{2\pi}{T}\left(t-\dfrac{L_{1}}{v}\right) $　$\cdots (3\ast)$

$\alpha-\beta= \dfrac{2\pi}{T}\left(t-\dfrac{L_{2}}{v}\right) $　$\cdots (4\ast)$

$(3\ast)+(4\ast)$を計算し，$\alpha$を求めます．

$2\alpha=\dfrac{2\pi}{T}\left(2t-\dfrac{L_{1}+L_{2}}{v}\right)$

$\therefore　\alpha=\dfrac{2\pi}{T}\left(t-\dfrac{L_{1}+L_{2}}{2v}\right)$　$\cdots (5\ast)$

$(3\ast)-(4\ast)$を計算し，$\beta$を求めます．

$2\beta=\dfrac{2\pi}{T}\cdot \dfrac{L_{2}-L_{1}}{v}$

$\therefore　\beta=\dfrac{2\pi}{T}\cdot \dfrac{L_{2}-L_{1}}{2v}$　$\cdots (6\ast)$

$(5\ast)$，$(6\ast)$を$(\clubsuit)$の右辺に代入して積の形をつくります．

$2\sin\left\{ \dfrac{2\pi}{T}\left(t-\dfrac{L_{1}+L_{2}}{2v}\right) \right\}\cos \left( \dfrac{2\pi}{T}\cdot \dfrac{L_{2}-L_{1}}{2v} \right)$

したがって，$(\sharp)$の式は

$y=2A \cos \left( \dfrac{2\pi}{T}\cdot \dfrac{L_{2}-L_{1}}{2v} \right) \sin\left\{ \dfrac{2\pi}{T}\left(t-\dfrac{L_{1}+L_{2}}{2v}\right) \right\} $

PHYさん

上式の$\sin$の部分は時間によって変化しますが，$\cos$の部分は時間によらず変化しません．

$\sin$より前の部分に絶対値をとったものが振幅となります．

振幅$=2A| \cos \left( \dfrac{2\pi}{T}\cdot \dfrac{L_{2}-L_{1}}{2v} \right) |$　(答)

(3)　

PHYさん

時間によらず変位$y$が0になるのは，振幅が$0$のときです．

すなわち，

$\cos \left( \dfrac{2\pi}{T}\cdot \dfrac{L_{2}-L_{1}}{2v} \right)=0$

のときなので，

$\dfrac{2\pi}{T}\cdot \dfrac{L_{2}-L_{1}}{2v}=\pm\dfrac{\pi}{2}，\pm\dfrac{3}{2}\pi，\pm\dfrac{5}{2}\pi ，\cdots $

整数$m$を用いて

$ \dfrac{2\pi}{T}\cdot \dfrac{L_{2}-L_{1}}{\cancel{2}v} =\dfrac{2m+1}{\cancel{2}}\pi$

波の基本式より，$vT=\lambda$であるから，

$\dfrac{2\pi}{\lambda}\cdot (L_{2}-L_{1})=(2m+1)\pi$

$\therefore　L_{2}-L_{1}=\left(m+\dfrac{1}{2}\right)\lambda$　(答)