
前回の内容はこちらです.
今回は,誘導なしだとやや難しいです.
ただ,誘導があれば,入試でも出てきます.
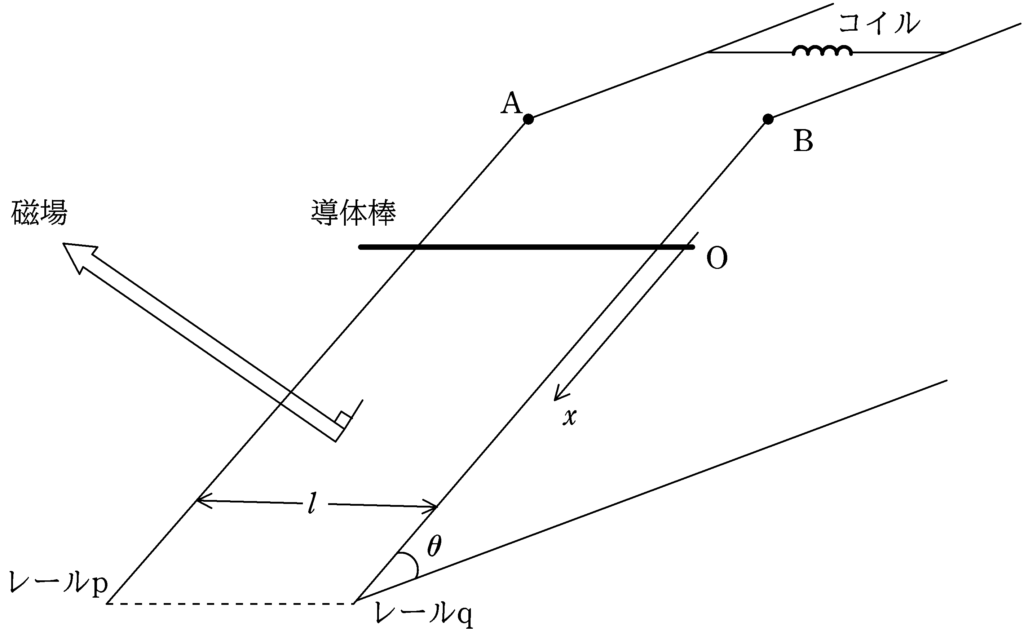
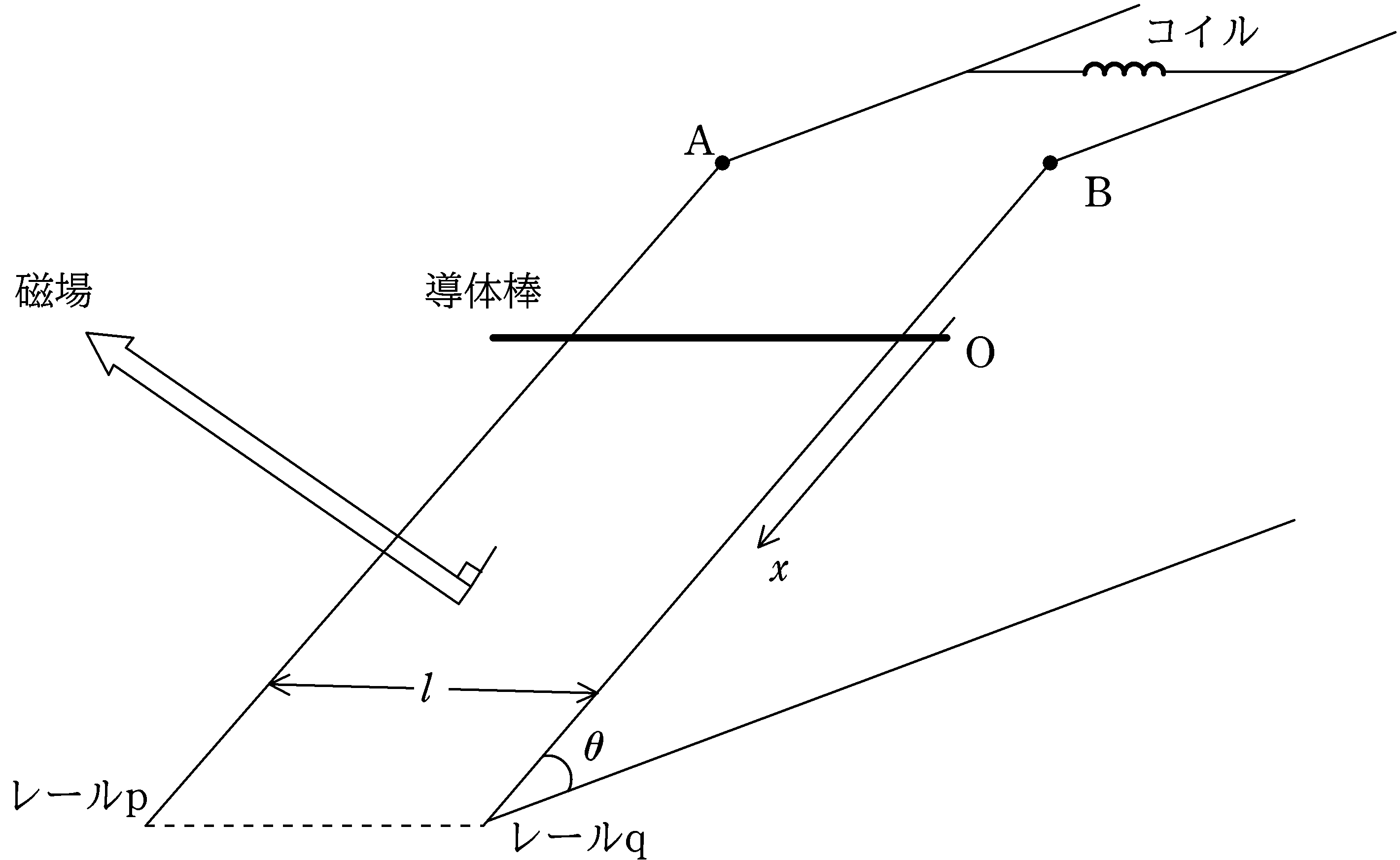
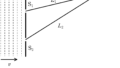
図のように,傾角$\theta$の斜面上に導体レールp,qが距離$l$を隔てて平行に固定されている.また,レールp,qは導線によって,自己インダクタンス$L$のコイルに接続されている.
図のように磁束密度の大きさ$B$の磁場を斜面に垂直な方向にかけ,質量$m$の導体棒をレールp,qに垂直になるように,静止させておく.静止した位置を原点として,斜面下向きに$x$座標をとる.
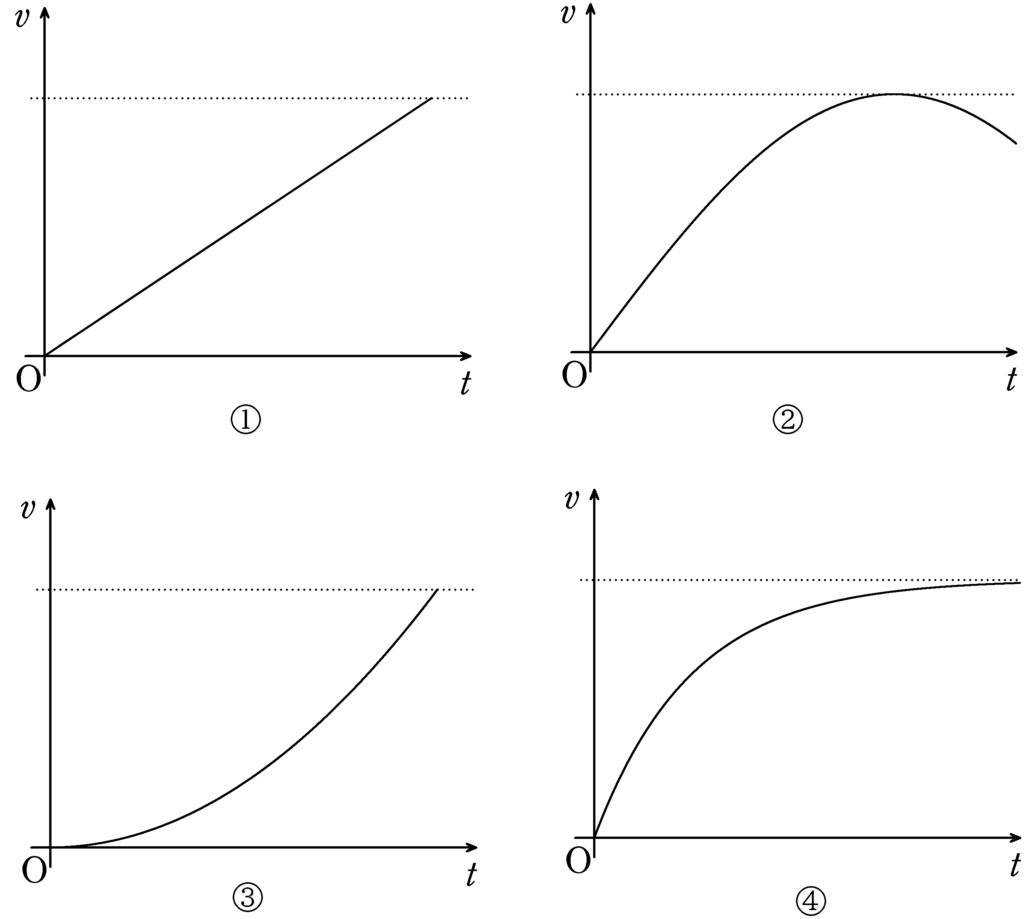
時刻を$0$のときに,導体棒のおさえをはずした.縦軸を導体棒の速度$v$,横軸を時刻$t$としたときのグラフとして適当なものを次の①~④の中から選べ.
ただし,導体棒とレールp,qの間に摩擦力がはたらかないとし,重力加速度の大きさを$g$とする.
PQ間に生じる誘導起電力の大きさ$V_{\rm{PQ}}$は,PQの長さを$l$,PQ方向に垂直な速さを$v_{\perp}$,導体棒が動く方向と垂直な磁束密度の大きさを$B$とすれば,
$V=v_{\perp}Bl$
- 回路の式(オームの法則,コンデンサーの基本式,電荷保存則など)
- 導体棒の運動に関する式(つり合いの式,運動方程式,運動量保存則など)
- 導体棒と回路の系全体のエネルギー収支の式

コイルの回路における扱いは次の記事を参考にしてください.
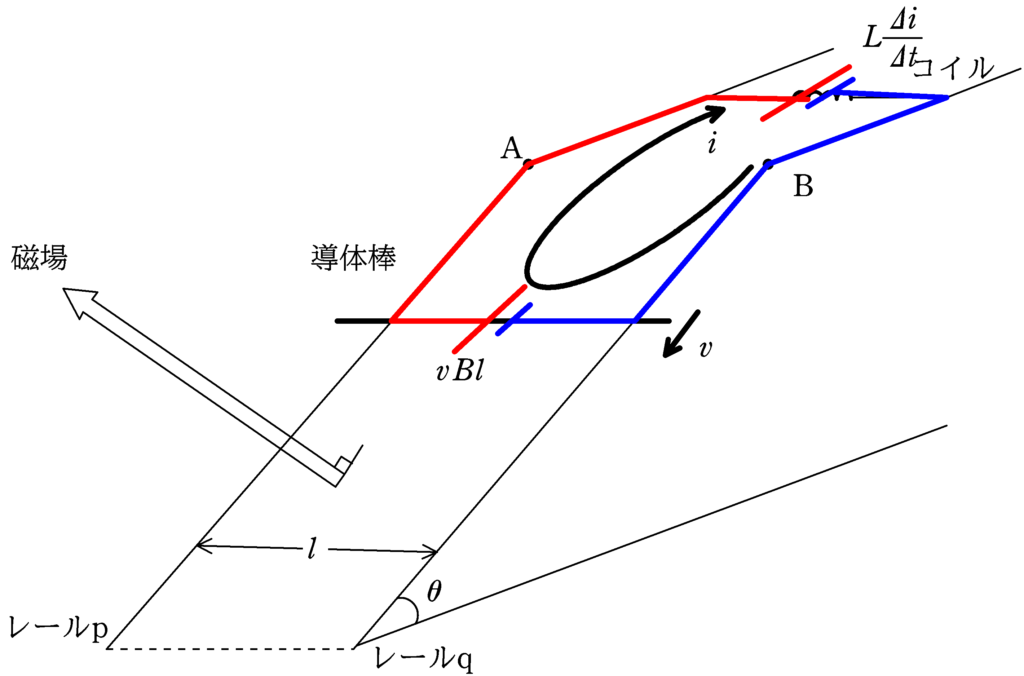

導体棒が速度$v$で動いているときは,$vBl$の誘導起電力が生じています.(図は速度が正のとき)
また,時間$\varDelta t$の間に電流が$\varDelta i$変化すると,コイルには$L\dfrac{\varDelta i}{\varDelta t}$が生じます.(図は電流の正の向きを図の矢印の向きとして,$\dfrac{\varDelta i}{\varDelta t}>0$のとき)
★ キルヒホッフ則
$vBl-L\dfrac{\varDelta i}{\varDelta t}=0$

上式において,
$v=\dfrac{\varDelta x}{\varDelta t}$
を代入して整理します.
$\dfrac{\varDelta x}{\cancel{\varDelta t}}\cdot Bl=L\dfrac{\varDelta i}{\cancel{\varDelta t}}$
$\therefore \dfrac{\varDelta i}{\varDelta x}=\dfrac{Bl}{L}=一定$

$ \dfrac{\varDelta i}{\varDelta x}=\dfrac{Bl}{L}=一定 $の意味を考えてみましょう.
これは,縦軸を$i$,横軸を$x$としたときの傾きに相当するね.時刻$0$において,$x=0$で,$i=0$でもあるから,原点を通る傾きが$\dfrac{Bl}{L}$の直線になるんだね.
大学入試では,積分を回避するためにこのようにグラフを利用して解くことがあるんだよ.
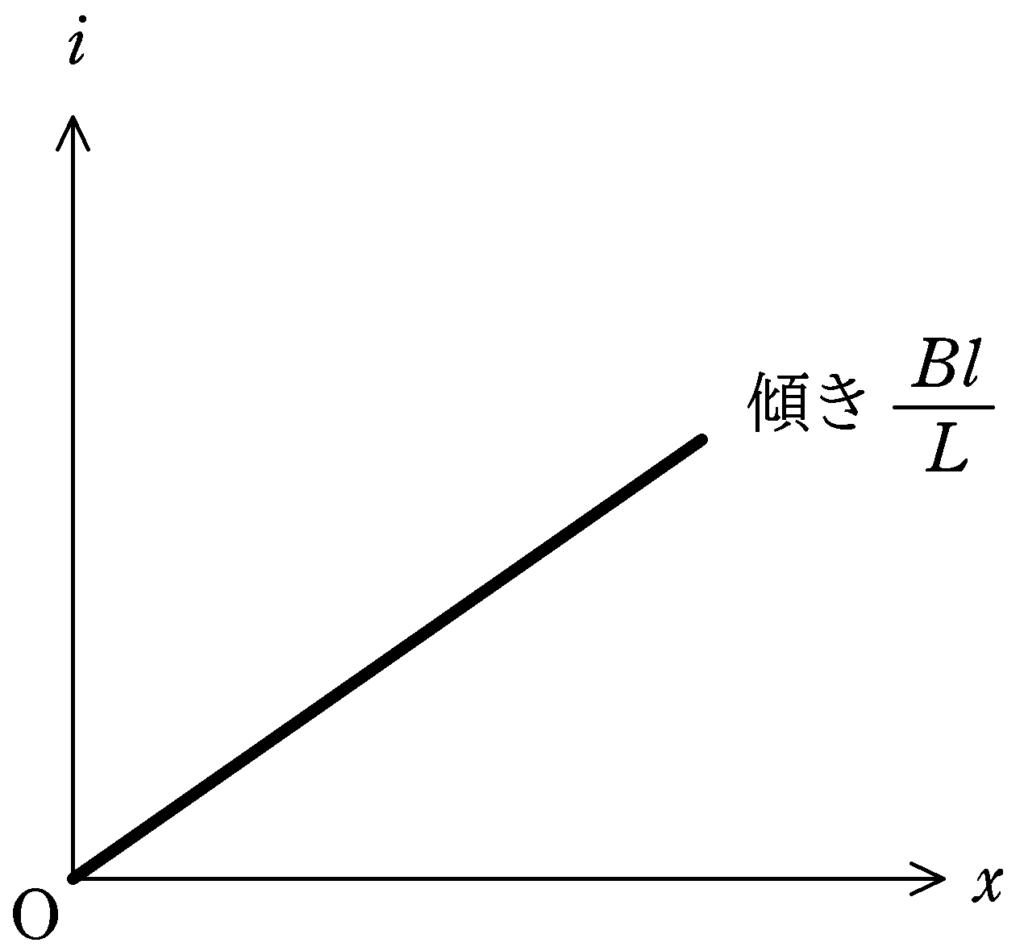

つまり,
$i=\dfrac{Bl}{L}x$ $\cdots (\ast)$
の関係があるんだね.

さらに運動方程式を立てます.
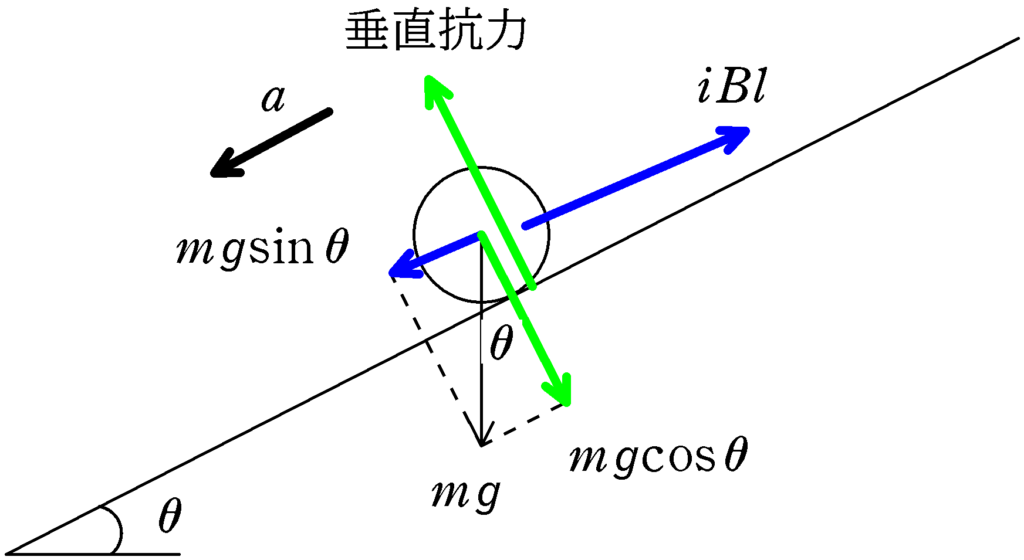
斜面下方向の加速度を$a$としましょう.
斜面下向きには,重力を分解した成分$mgsin\theta$が,斜面真上からみて反時計回りを電流の向きとしたとき,斜面上向きには電磁力$iBl$がはたらきます.
★ 運動方程式
$ma=mg\sin\theta-iBl$ $\cdots (2\ast)$

$(\ast)$を$(2\ast)$に代入して$i$を消去しましょう.
$\eqalign{ma&=mg\sin\theta-iBl\\&=mg\sin\theta-\dfrac{B^{2}l^{2}}{L}x\\&=-\dfrac{B^{2}l^{2}}{L}\left(x-\dfrac{mgL\sin\theta}{B^{2}l^{2}}\right) \cdots (3\ast)} $

この運動方程式は単振動だね.
単振動の演習はこちらにまとめてあるので,単振動が苦手な人は練習しておきましょう.
質量を$m$,加速度を$a$,物体の座標を$x$,$x_{0}$を定数,$k$を正の定数とする.
運動方程式が以下で表されている.
$ma=-k(x-x_{0})$
このとき,振動の中心は$x_{0}$,角振動数$\omega$と周期$T$は次のようになる.
$\omega=\sqrt{\dfrac{k}{m}}$
$T=\dfrac{2\pi}{\omega}=2\pi\sqrt{\dfrac{m}{k}}$

$(3\ast)$の運動方程式から,振動の中心は$x= \dfrac{mgL\sin\theta}{B^{2}l^{2}} $,角振動数$\omega$は
$\omega=\sqrt{\dfrac{B^{2}l^{2}}{mL}}=\dfrac{Bl}{\sqrt{mL}}$
の単振動をするんだね.$x=0$において$v=0$になるので,ここが振動の下端(座標としては一番小さい)になって,中心までの距離は$ \dfrac{mgL\sin\theta}{B^{2}l^{2}} $なのでこれが振幅になるね.
だから,時刻$t$における位置$x$は
$x= \dfrac{mgL\sin\theta}{B^{2}l^{2}} – \dfrac{mgL\sin\theta}{B^{2}l^{2}} \cos \left( \dfrac{Bl}{\sqrt{mL}} t\right)$
であって,これを$t$で微分すると
$v=\dfrac{dx}{dt}=\dfrac{g\sin\theta\sqrt{mL}}{Bl}\sin\left(\dfrac{Bl}{\sqrt{mL}}t\right)$
となるからから,$\sin$のグラフを選べばいいね.
したがって,答えは②(答)です.



コメント