水平でなめらかな床の上に質量$m_{1}$の物体$\rm A$と質量$m_{2}$の物体$\rm B$がある.静止している物体$\rm B$に速さ$v_{0}$の物体$\rm A$を衝突させる.$\rm A$と$\rm B$のはねかえり係数を$e$として,次の問いに答えよ.
(1) 衝突直後の$\rm A$と$\rm B$の速度をそれぞれ$v_{1}$,$v_{2}$とする.このとき,運動量保存則とはねかえり係数の式を立てよ.
(2) (1)より$v_{1}$,$v_{2}$を$m_{1}$,$m_{2}$,$v_{0}$を用いて表せ.
<解答>

運動量保存則とはねかえり係数の式を確認しましょう.
質量$m_{1}$の物体1と質量$m_{2}$の物体2の速度を$v_{1}$,$v_{2}$とする.
物体1と物体2の力積の和が0のとき,次の式が成り立つ.
$m_{1}v_{1}+m_{2}v_{2}=$一定
これを運動量保存則という.
運動量保存則は次のようなときに立てることが多い.
.2つ以上の物体の運動
・水平方向の成分の力の和が0のとき
・鉛直方向であっても,空中衝突や空中分裂などの,非常に短い時間で外力がはたらく場合は,近似的に運動量保存則を立てる.
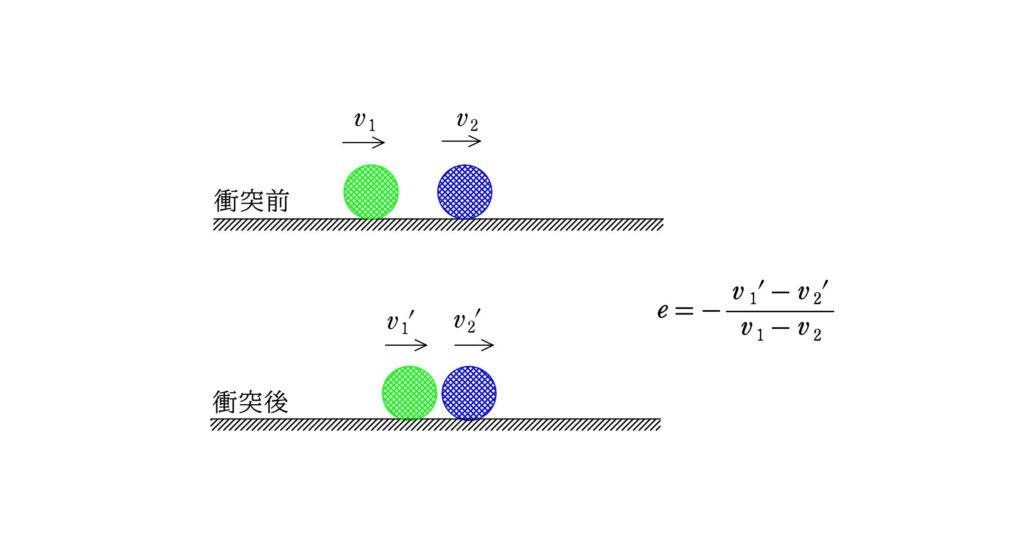
衝突前の物体の速度を$v_{1}$,$v_{2}$,衝突後の速度を$v_{1}^{\prime}$,$v_{2}^{\prime}$とするとき,はねかえり係数(反発係数)の式を次のように定義する.
$e=-\dfrac{v_{1}^{\prime}-v_{2}^{\prime}}{v_{1}-v_{2}}$
$e=1$のときを弾性衝突といい,力学的エネルギーが保存する.
また,$e=0$のときを完全非弾性衝突という.
★ 運動量保存則より
$m_{1}v_{0}=m_{1}v_{1}+m_{2}v_{2}$ $\dots (\ast)$ (答)
★ はねかえり係数の式
$e=-\dfrac{v_{1}-v_{2}}{v_{0}-0}$ $\dots (2\ast)$ (答)
(2)

$(2\ast)$より
$v_{2}=v_{1}+ev_{0}$ $\dots (3\ast)$
と変形して,$(\ast)$に代入しましょう.
$\eqalign{m_{1}v_{0}&=m_{1}v_{1}+m_{2}(v_{1}+ev_{0})\cr (m_{1}+m_{2})v_{1}&=(m_{1}-em_{2})v_{0}\cr v_{1}&=\dfrac{m_{1}-em_{2}}{m_{1}+m_{2}}v_{0}}$ (答)
これを$(3\ast)$に代入すると
$\eqalign{v_{2}&=\dfrac{m_{1}-em_{2}}{m_{1}+m_{2}}v_{0}+ev_{0}\\&=\left(\dfrac{m_{1}-em_{2}}{m_{1}+m_{2}}+\dfrac{em_{1}+em_{2}}{m_{1}+m_{2}}\right)v_{0}\\&=\dfrac{(e+1)m_{1}}{m_{1}+m_{2}}v_{0}}$ (答)


コメント