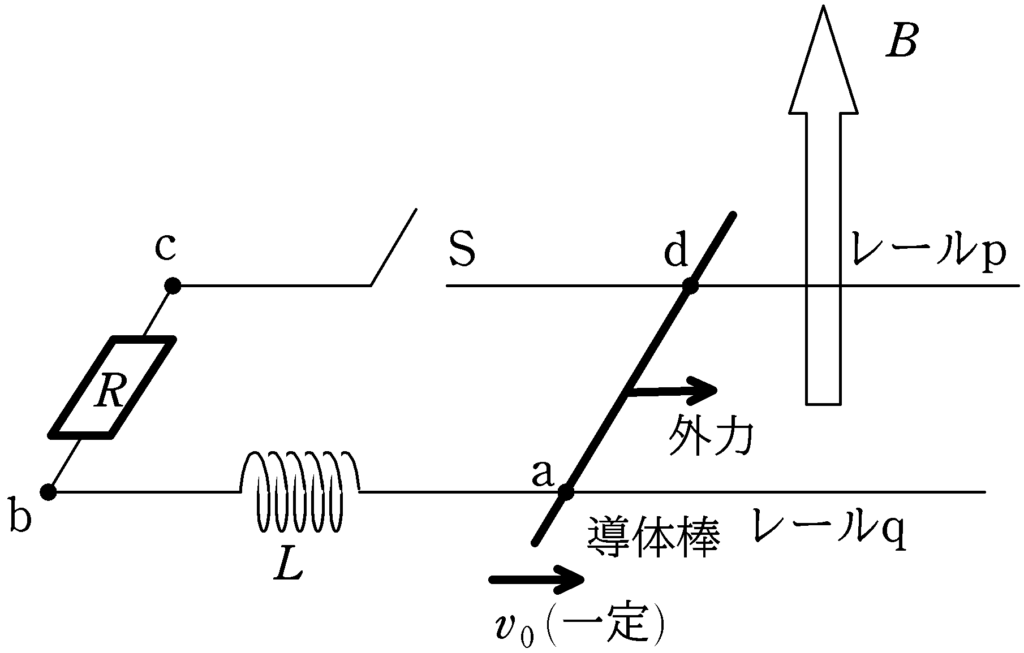
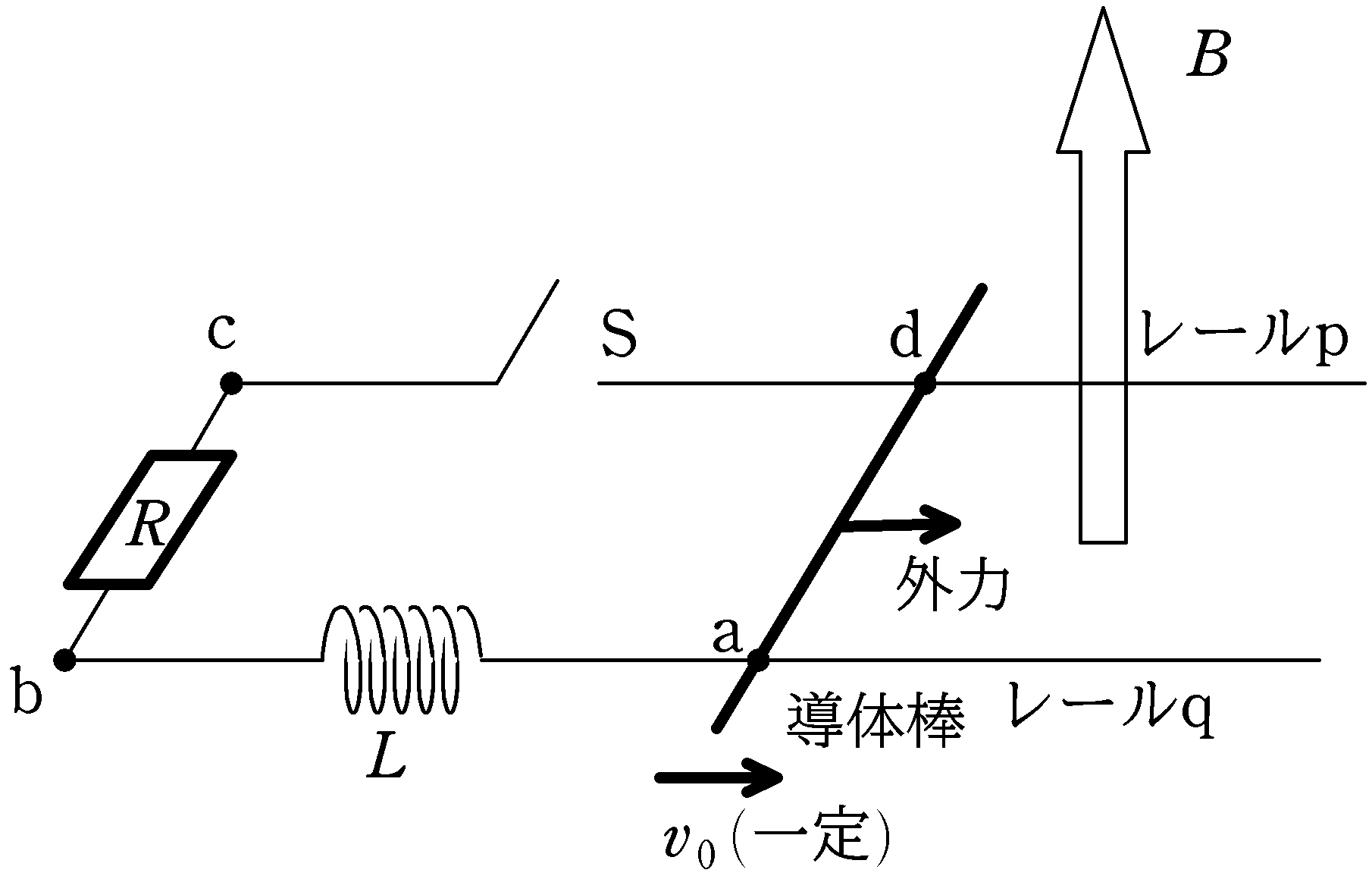
図のように，水平面に固定された導体レールp，qがある．導体レールは距離$l$を隔てて平行に設置されており，導体レールには，スイッチS，抵抗$R$の電気抵抗，自己インダクタンス$L$のコイルが接続されている．磁束密度の大きさ$B$の一様な磁場を鉛直上向きにかけた状態で質量$m$の導体棒をレールと垂直においた．スイッチが開かれた状態で導体棒に外力を加え，常に導体棒の速度を図の向きに一定の$v_{0}$になるようにした．
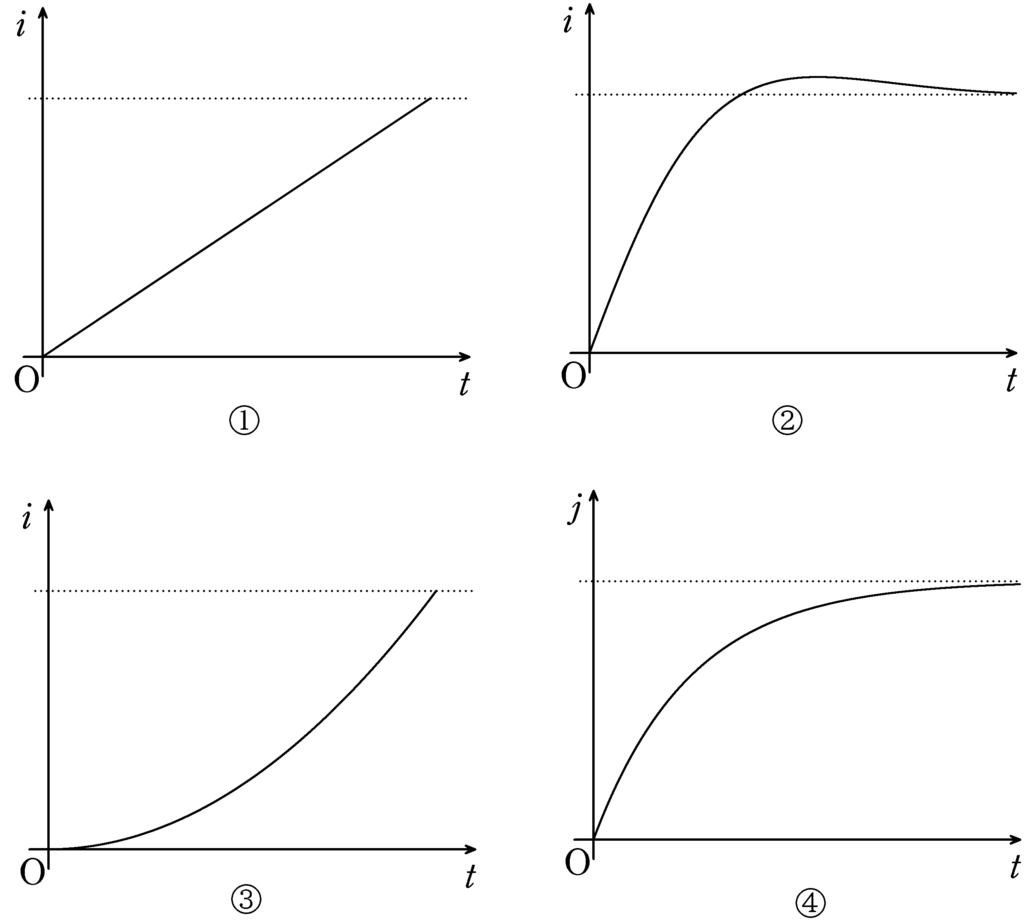
スイッチSを閉じた直後の時刻を$0$として，縦軸を回路に流れる電流$i$，横軸を時刻$t$としたときのグラフとして適切なものを次の中から選べ．ただし，a→b→c→dを電流の正の向きとする．
PQ間に生じる誘導起電力の大きさ$V_{\rm{PQ}}$は，PQの長さを$l$，PQ方向に垂直な速さを$v_{\perp}$，導体棒が動く方向と垂直な磁束密度の大きさを$B$とすれば，
$V=v_{\perp}Bl$
- 回路の式（オームの法則，コンデンサーの基本式，電荷保存則など）
- 導体棒の運動に関する式（つり合いの式，運動方程式，運動量保存則など）
- 導体棒と回路の系全体のエネルギー収支の式
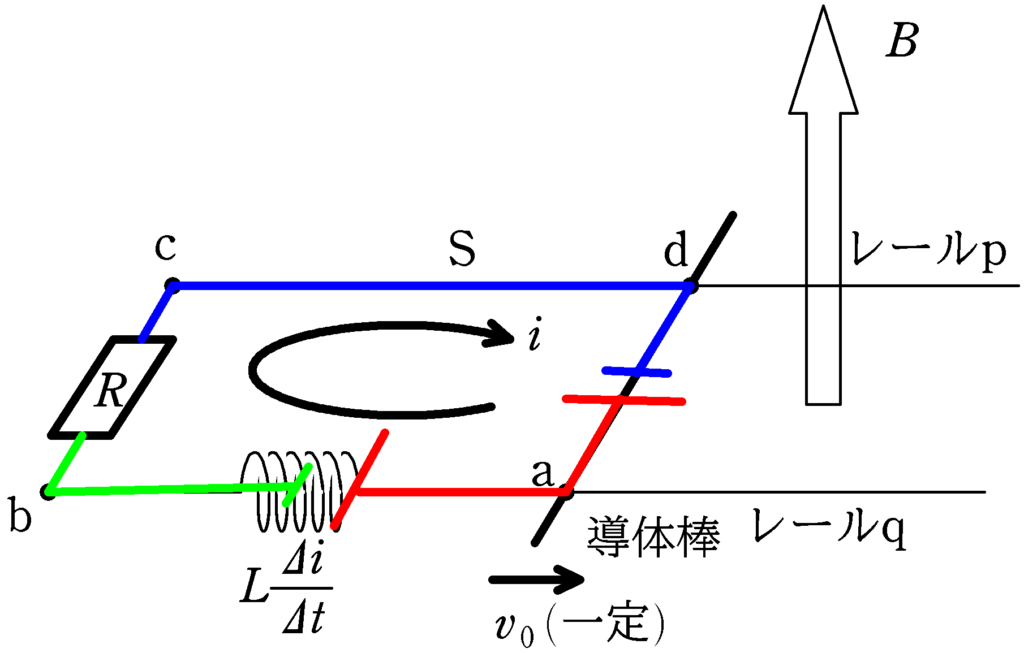
導体棒に生じる誘導起電力は$v_{0}Bl$で向きは上図のようになります．
また，流れる電流を$i$とすると，コイルに生じる誘導起電力は図のように$-L\dfrac{\varDelta i}{\varDelta t}$となります．
キルヒホッフ則を立てましょう．
★ キルヒホッフ則
$v_{0}Bl-L\dfrac{\varDelta i}{\varDelta t}-Ri=0$
$\therefore L\dfrac{\varDelta i}{\varDelta t}=-Ri+v_{0}Bl$ $\cdots (\ast)$
これは，運動方程式ではないけど，「終端速度型」だね．
「終端速度型」は$t=0$のときと$t=\infty$について考えます．
質量を$m$，加速度を$a$，速度を$v$，$C$を定数とすると
$ma=-kv+C$
は終端速度型の運動方程式である．
終端速度型の運動方程式は次の特徴がある．
十分時間が経つと，速度が一定（加速度が0）になる．
速度が一定になったときの速度を終端速度という．
終端速度は運動方程式に$a=0$を代入して
$0=-kv+C$ $\therefore v=\dfrac{C}{k}$
また，$t=0$のときの速度を$v_{0}$とすると，そのときの加速度（$v-t$グラフの傾き）は
$a=\dfrac{-kv_{0}+C}{m}$
となる．
$t=0$のときは$i=0$なので
$\dfrac{\varDelta i}{\varDelta t}=\dfrac{v_{0}BL}{L}\,(>0)$
なので，電流が少しずつ流れはじめるんだね．
しかし，電流が大きくなっていくと，少しずつ$\dfrac{\varDelta i}{\varDelta t}$が小さくなっていきます．
そして，十分時間が経つと$\dfrac{\varDelta i}{\varDelta t}=0$となり，$(\ast)$より
$0= -Ri+v_{0}Bl$
$\therefore i=\dfrac{v_{0}Bl}{R}$
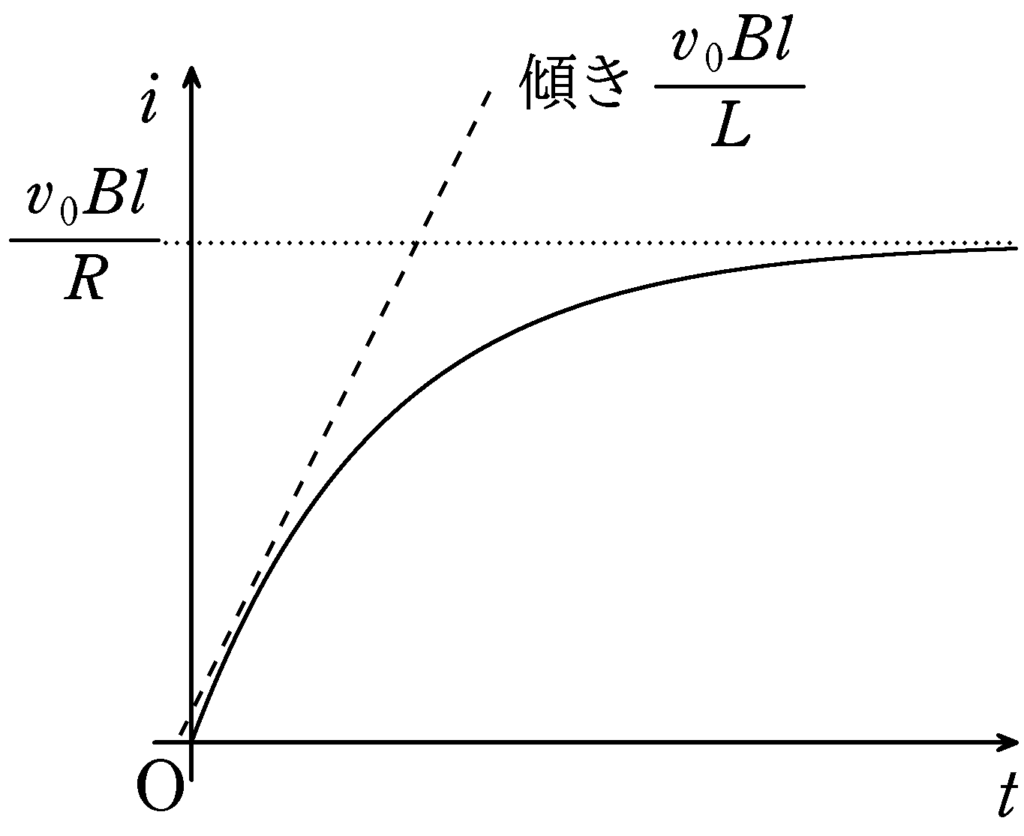
十分時間が経過すると，一定電流$i= \dfrac{v_{0}Bl}{R} $が流れます．また，$\dfrac{\varDelta i}{\varDelta t}=0$なので，もう電流は変化しません．
したがって，答えは④（答）です．
コメント
[…] 導体棒のグラフ対策6PHYさん前回の内容はこちらです．問題図のように，水… […]