
今回はベータトロンの実践演習です.
ベータトロンの基本は下の記事で扱っています.
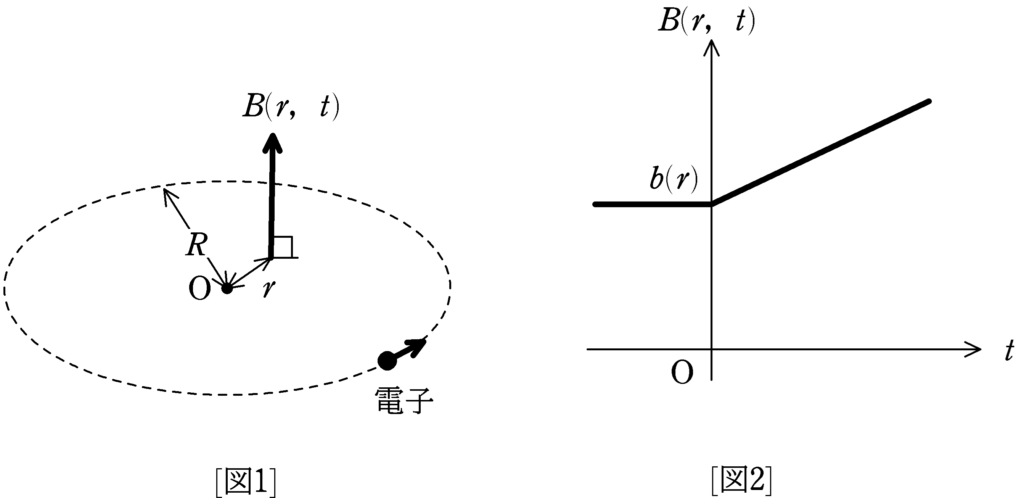
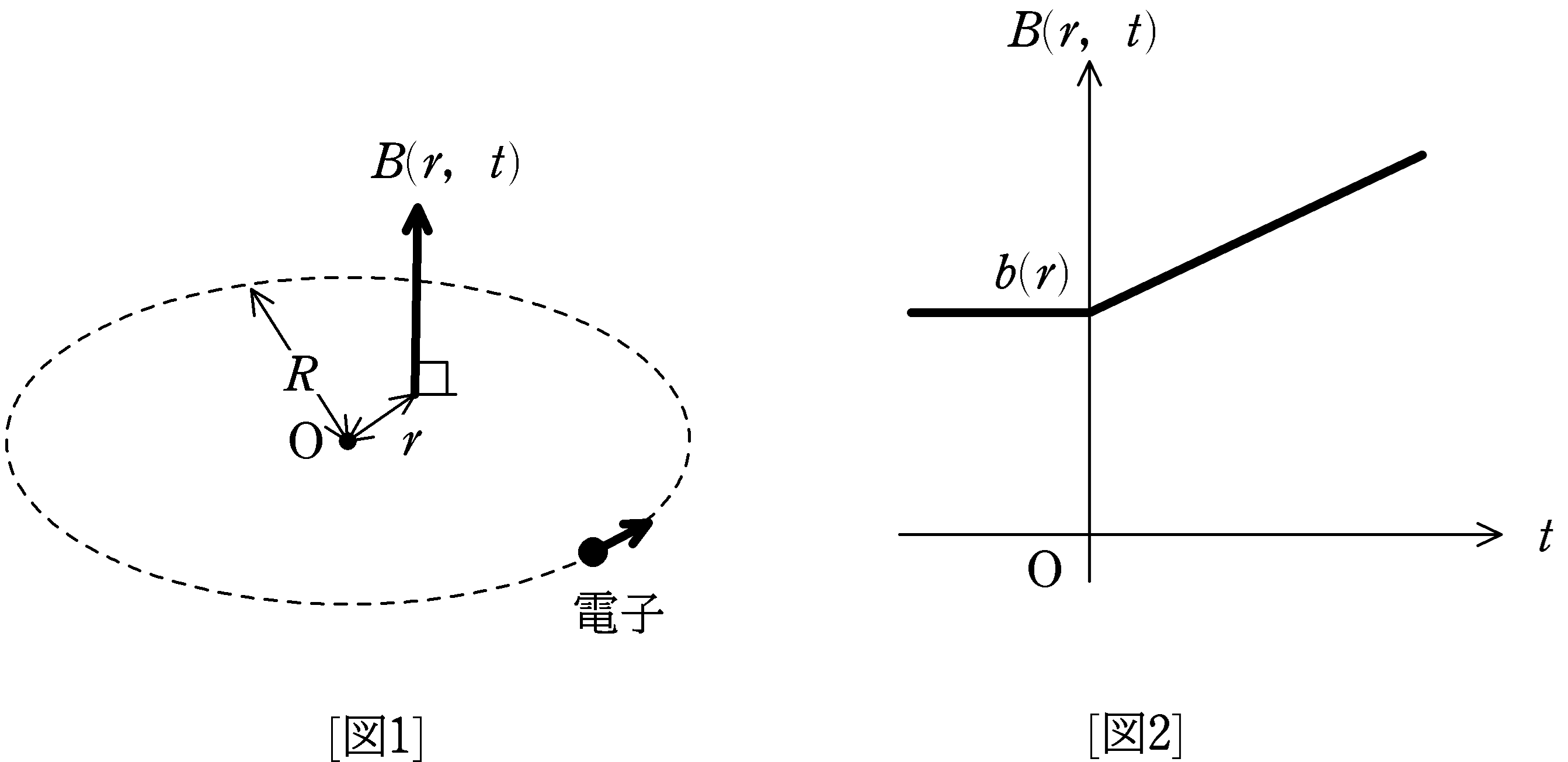
[図1]のように鉛直上方向に向いた磁場に垂直な質量$m$,電荷$-e$の電子の円運動について考える.ただし,$e>0$である.磁束密度$B$が[図1]のようにOより距離$r$の値に依存し,時刻$t<0$では時間によらず,時刻$t\geqq 0$では時間とともに増加する場合を考える.この磁束密度を$B(r,t)$と表す.
$B(r,t)=\begin{cases}b(r) &(t<0)\\b(r)\left(1+\alpha t\right) &(t\geqq 0)\end{cases}$
ただし,$\alpha$は正の定数であり,$b(r)$は正の値をもち,$r$とともに単調に変化するものとする.
$t<0$のある時刻に[図1]の向きに速さ$v_{0}$の初速度を電子に与えたところ,磁場と垂直な平面内で原点Oを中心とする半径$R$の円を描いた.$t\geqq 0$になっても電子は$t<0$の場合と同じ半径$R$の円運動を続けた.このとき,以下の問いに答えよ.
(1) 原点Oを中心とした半径$r$と$r+dr$で囲まれた薄い膜の部分の磁束は
$B(r)\times 2\pi r dr=2\pi(1+\alpha t)b(r)rdr$
であるから,これを$0$から$R$まで足し合わせると,半径$R$の円内部の磁束$\varPhi(t)$は
$\eqalign{\varPhi(t)&=2\pi(1+\alpha t)\int_{0}^{R}b(r)rdr\\&=\phi(R)(1+\alpha t)}$
ただし,$\phi(R)=2\pi\int_{0}^{R}b(r)rdr$とした.このとき,誘導起電力の大きさ$V$を$\phi(R)$,$\alpha$を用いて表せ.
(2) 正の時刻$t$での電子の速度を$v_{0},R,\phi(R),\alpha,m,e,t$を用いて表せ.
(3) 正の時刻$t$での電子の速度が$v$のとき,向心方向の運動方程式を立てることで,速度$v$を$e,R,m,\alpha,b(R),t$を用いて表せ.
(4) (2)と(3)より,$b(R)$を$m,v_{0},e,R$を用いて表せ.また,$\phi(R)$と$b(R)$の関係式を答えよ.
<解答>
(1)

ファラデーの電磁誘導の法則を使います.
$\varDelta t$の間に磁束が$\varDelta \varPhi$変化するときに生じる誘導起電力の大きさ$V$は
$V=|\dfrac{\varDelta \varPhi}{\varDelta t}|$
ファラデーの電磁誘導の法則より
$\eqalign{V&=\dfrac{\varDelta \varPhi(t)}{\varDelta t}\\&=\dfrac{\varDelta }{\varDelta t}\left\{\phi(R)(1+\alpha t)\right\}\\&=\alpha\phi(R)}$
したがって,$V=\alpha\phi(R)$
(2)

今,時間とともに半径$R$の円の内部の磁束は増加しているので,レンツの法則より,この磁束が減るような起電力が周上にできます.
右手親指を下向きに向けると,周上には上からみてと時計回りの誘導起電力が生じることが確認できます.
そして,誘導起電力の方向に誘導電場も生じています.
電場と電位差の関係より,電場を計算していきましょう.
電場の大きさを$E$,距離$\Delta x$の電位差を$\Delta V$とするとき,次の関係が成り立つ.
$E=\left|\dfrac{\Delta V}{\Delta x}\right|$
半径$R$の円周上の電場の大きさを$E$とすると,電場と電位差の関係より
$E=\dfrac{V}{2\pi R}=\dfrac{\alpha \phi(R)}{2\pi R}$

$R,\alpha,\phi(R)$は時間によって変化しないので,円周上の電場は時間によらず一定です.
時間によらず一定の電場がかかっているので,半径$R$の円周上を円運動している電子には,一定の力がはたらくことになります.一定の力がはたらくということは,加速度が一定の等加速度運動をします.
電子の電荷は$-e$なので,電場の方向とは逆,つまり,初速度$v_{0}$の方向とは同じ方向にクーロン力を受けます.
★ クーロン力の大きさ$F$
$F=eE=\dfrac{e\alpha \phi(R)}{2\pi R}$
★ 接線方向の運動方程式
電子の接線方向の加速度を$a$として,運動方程式は
$ma=\dfrac{e\alpha \phi(R)}{2\pi R}$ $\therefore\,\, a=\dfrac{e\alpha \phi(R)}{2\pi Rm}$

接線方向について,等加速度運動の式から時刻$t$における速度$v$を求めることができます.
★ 等加速度運動の式
$v=v_{0}+at=v_{0}+\dfrac{e\alpha \phi(R)}{2\pi Rm}t$ (答) $\cdots (\ast)$
(3)

一方,電子は半径$R$の円運動を続けているという条件から向心方向の運動方程式を立てることができます.
向心力はローレンツ力です.
$r=R$における磁束密度は
$B(R,t)=b(R)(1+\alpha t)$
なので,ローレンツ力の大きさ$f$は
$f=evB(R,t)=evb(R)(1+\alpha t)$
となります.
★ 向心方向の運動方程式
$m\dfrac{v^{\cancel{2}}}{R}=e\cancel{v}b(R)(1+\alpha t)$
$\therefore\,\, v=\dfrac{eRb(R)}{m}+\dfrac{eR\alpha b(R)}{m}t$ (答) $\cdots (2\ast)$
(4)

$(\ast)$,$(2\ast)$の定数項の部分と$t$の係数部分の比較を行います.
$(\ast)$:$v=v_{0}+at=v_{0}+\dfrac{e\alpha \phi(R)}{2\pi Rm}t$
$(2\ast)$:$v=\dfrac{eRb(R)}{m}+\dfrac{eR\alpha b(R)}{m}t$
比較して
$v_{0}=\dfrac{eRb(R)}{m}$ $\cdots (3\ast)$
$\dfrac{e\alpha \phi(R)}{2\pi Rm}=\dfrac{eR\alpha b(R)}{m}$ $\cdots (4\ast)$
$(3\ast)$より
$b(R)=\dfrac{mv_{0}}{eR}$ (答)
$(4\ast)$より
$\phi(R)=2\times \pi R^{2}b(R)$ (答)

$\phi(R)=2\times \pi R^{2}b(R)$はベータトロン条件($\varPhi(t) =2\times \pi R^{2}B(R,t)$でもあります)です.
また,$b(R)=\dfrac{mv_{0}}{eR}$より,
$b(r)=\dfrac{mv_{0}}{eR}$
が推定できます.
つまり,Oから$r$の距離における磁束密度は$r$に反比例していることがわかります.

難しい計算が多いけど,やっていることは
- 接線方向に誘導起電力が生じることから,誘導電場を求め,静電気力の大きさを求め,速度を計算する.
- 半径一定の円運動をしている条件から向心方向の運動方程式を立てて速度を求める.
- 1と2が同じ速度であることから,ベータトロン条件を求める.
という典型的な問題なんだね.


コメント