
今回は,京都大にも出題されていた
「一様ではない磁場中の回転棒に生じる起電力」
の計算問題を扱います.
微分積分を使わなくとも解けるようになっています.
一様な磁場がかかっている基本的な問題はこちらです.
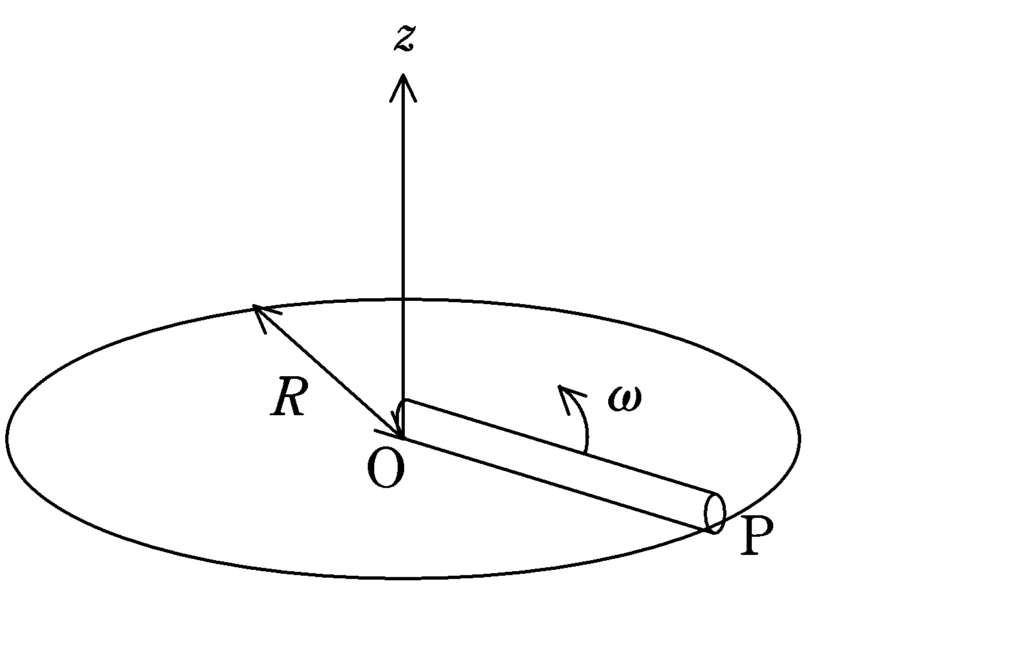
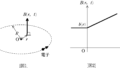
上図のように,$z$軸をとり,$z$軸の正方向に,$z$軸に関して対称な磁場がある.原点Oより距離$r$における磁束密度$B(r)$は次のようになる.
$B(r)=\begin{cases}-\dfrac{B_{0}}{R}r+B_{0} &(0\leqq r<R)\\0&(R\leqq r) \end{cases}$
ただし,$B_{0},R$は正の定数である.このような磁場中で長さ$R$の導体棒をOを中心に一定の角速度$\omega$で回転させる.このとき,次の問いに答えよ.
(1) 導体棒中のOより距離$r$の位置にある電子について考える.電子の電荷を$-e$,Oより距離$r$の位置の電場を$E(r)$として,電子とともに回転した観測者からみた電子にはたらく静電気力とローレンツ力の(遠心力は無視する.)つり合いの式から,$E(r)$を$B_{0},R,\omega,r$を用いて表せ.
(2) 縦軸を$E(r)$,横軸を$r$としたグラフをかき,グラフと$r$軸で囲まれた面積を計算することで,導体棒の両端の電位差$V$を$B_{0},\omega,R$を用いて表せ.
<解答>
(1)
磁場の大きさを$B$,磁場に垂直な速度の大きさを$v$,荷電粒子の電荷を$q$のとき,荷電粒子が受けるローレンツ力の大きさ$f$は
$f=|q|vB$
向きはフレミング左手の法則に従う.
$\clubsuit$フレミング左手の法則$\clubsuit$
親指→ローレンツ力の向き
人差し指→磁場の向き
中指→電流の向き(正電荷の動く向き,負電荷の動く向きと逆)
電場の大きさ$E$の場所に電荷$q$をおいたときにはたらく静電気力の大きさ$F$は
$F=|q|E$

Oより,距離$r$にある電子の接線方向の速さは$r\omega$です.
するとローレンツ力は
左手中指→下図$r\omega $の方向と逆
左手人差し指→紙面奥から手前方向
に向けると,左手親指はOの方向になるので,ローレンツ力はOに向かう向きです.
電子がつり合うには,静電気力がローレンツ力とは逆方向にはたらく必要があります.したがって,静電気力はPの方向となります.
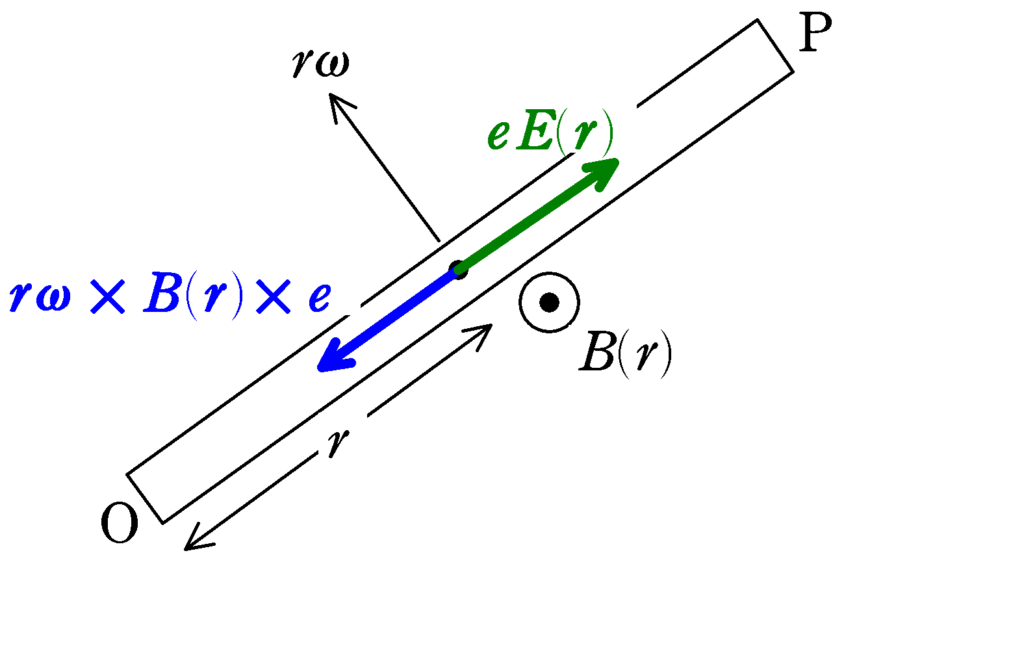
★ 静電気力とローレンツ力のつり合いの式
$r\omega \times B(r)\times \cancel{e}=\cancel{e}E(r)$
$B(r)=-\dfrac{B_{0}r+B_{0}}{R}$より
$E(r)=r\omega\left(-\dfrac{B_{0}}{R}r+B_{0}\right)=-\dfrac{B_{0}\omega }{R}r(r-R)$ (答)
(2)

下図が
$E(r)=-\dfrac{B_{0}\omega }{R}r(r-R)$
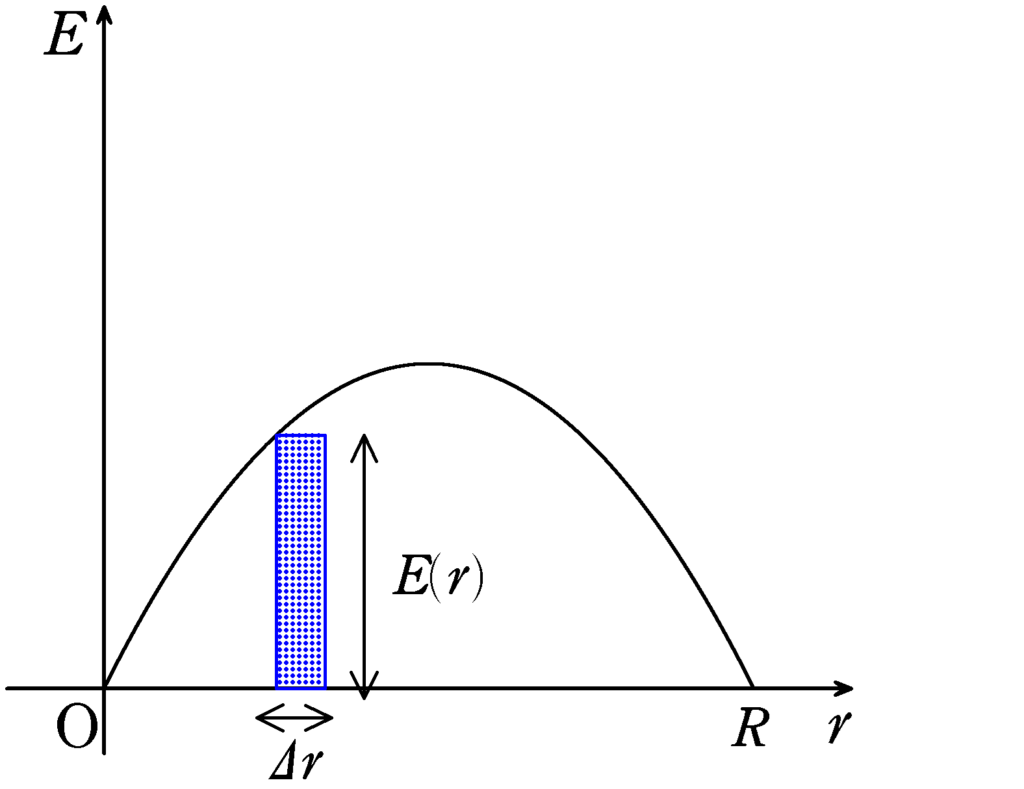
のグラフです.下図の長方形の面積は
$E\varDelta r$
であり,これがちょうど$\varDelta r$離れた場所での電位差を意味しているので,面積を求めることで,OP間の電位差を計算することができます.
電場の大きさを$E$,距離$\Delta x$の電位差を$\Delta V$とするとき,次の関係が成り立つ.
$E=\left|\dfrac{\Delta V}{\Delta x}\right|$
$\eqalign{V&=-\dfrac{B_{0}\omega}{R}\int_{0}^{R}r(r-R)dr\\&=-\dfrac{B_{0}\omega}{R}\cdot \left\{-\dfrac{(R-0)^{3}}{6}\right\}\\&=\dfrac{B_{0}\omega R^{2}}{6}}$
したがって,OP間の起電力の大きさは$\dfrac{B_{0}\omega R^{2}}{6}$(答)

定積分の計算は$1/6$公式
$\int_{\alpha}^{\beta}(x-\alpha)(x-\beta)dx=-\dfrac{(\beta-\alpha)^{3}}{6}$
を使いました.



コメント
設問の誘導を無視して、中心からr離れた部分の時間当たりの面積の変化量とその部分での磁場の大きさの積を、r=0~Rで積分して、誘導起電力を出して(2)の答えとしたのですが、これは間違っていないですか?
間違っていないです!