
この前導体棒の磁場中の運動の問題を解いていたら,導体棒が磁場を垂直に切る速さ$v_{\perp}$,磁束密度の大きさ$B$,導体棒の長さを$l$としたときの導体棒に生じる誘導起電力の大きさ$V$の式
$V=v_{\perp}Bl$
が使えない式に出会ったんだ...
PQ間に生じる誘導起電力の大きさ$V_{\rm{PQ}}$は,PQの長さを$l$,PQ方向に垂直な速さを$v_{\perp}$,導体棒が動く方向と垂直な磁束密度の大きさを$B$とすれば,
$V=v_{\perp}Bl$

どんな問題ですか?

導体棒が円運動をする問題.
下図のように,長さ$l$の導体棒が磁束密度$B$中でPを中心に角速度$\omega$で等速円運動をしているときの誘導起電力$V$を求めよ,という問題だったんだけど,,
半径$r$,角速度$\omega$の円運動の速さ$v$は
$v=r\omega$
だからてっきり誘導起電力$V$は
$V=vBl=l\omega Bl=l^{2}\omega B$
だと思ったんだけど,なぜか答えが
$V=\dfrac{1}{2}l^{2}\omega B$
だったんだ・・・.
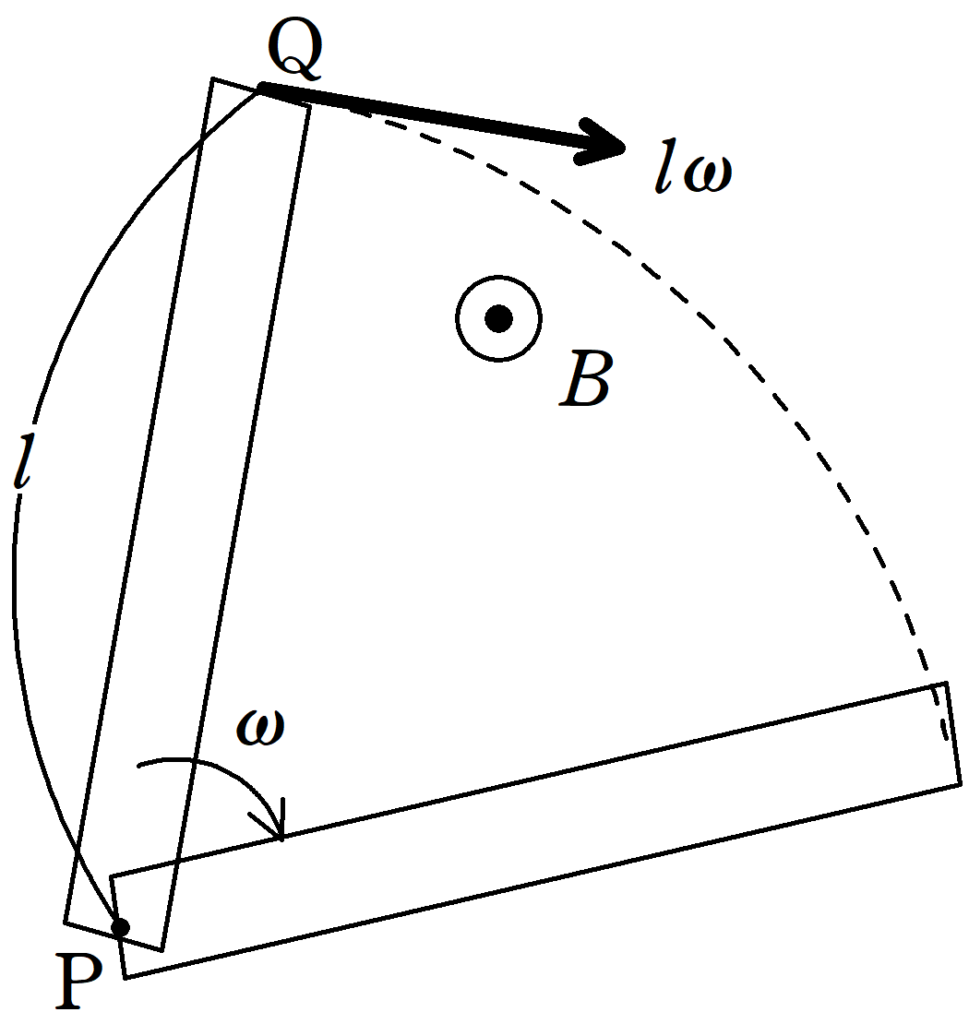

そうですね.それはよくみる間違いです.実際,導体棒は各場所で速さが異なりますよね?
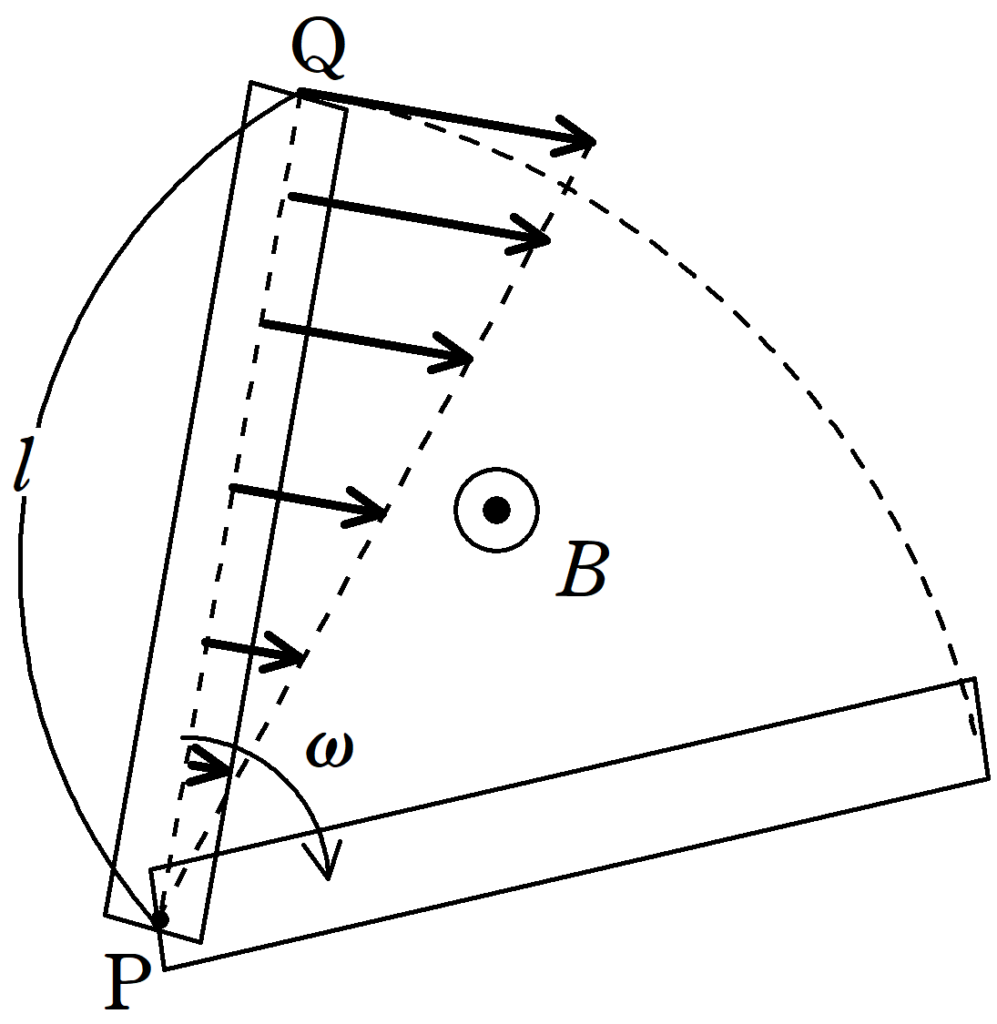

そうか!Pに近いところは速度の大きさが小さいから誘導起電力も小さいけど,Pから遠いところでは速度の大きさが大きいから誘導起電力が大きくなるんだ.場所によって誘導起電力が違うから分割して起電力を足し合わせなくちゃいけないんだね!

そういうことです.
それでは,PQ間に生じる起電力を計算するために,Pから距離$x$離れた場所のローレンツ力を計算してみましょう.
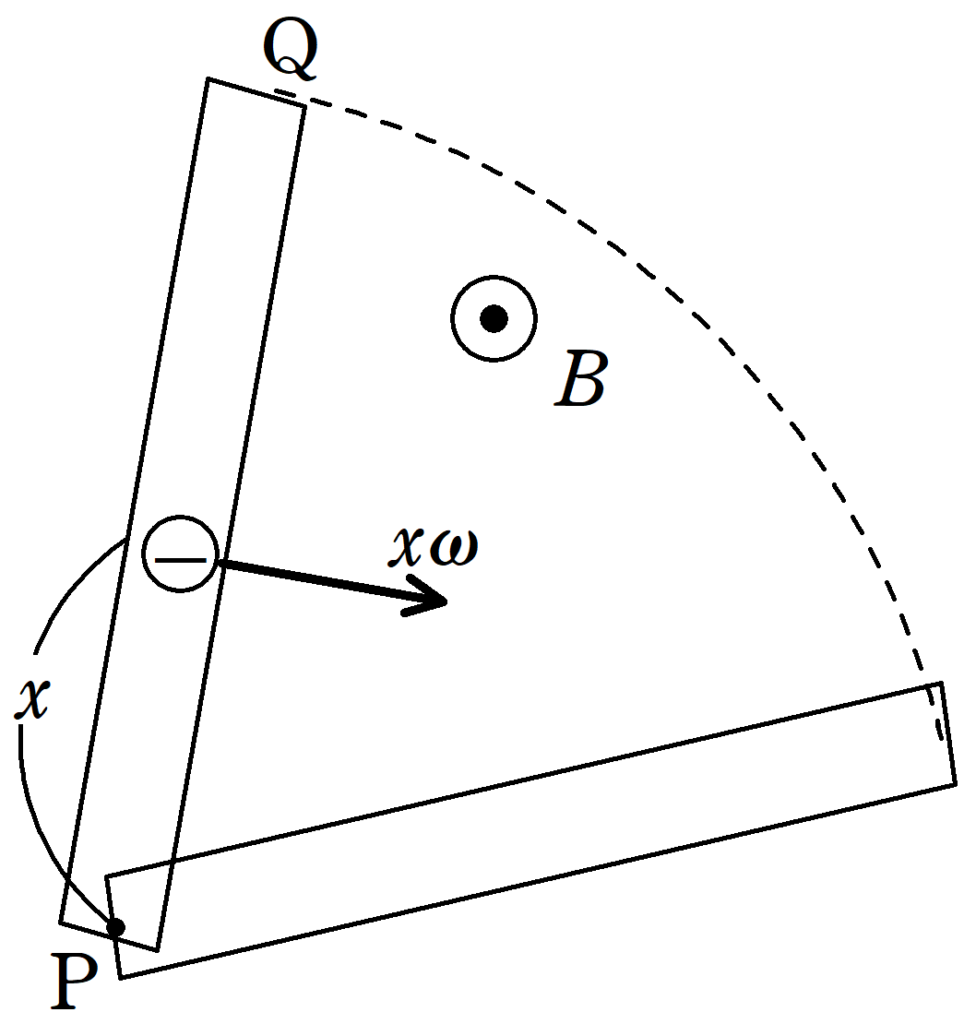

中心Pからの距離が$x$の場所の円運動の速さは$v=x\omega$だね.電子の電荷を$-e$とするとローレンツ力の大きさ$f$は
$f=evB=ex\omega B$
だね.向きはフレミング左手の法則からP→Qの向きだね.

はい,そして
と同じように,クーロン力とのつり合いを考えます.

Pから距離$x$での電場を$E$とすると,クーロン力は$eE$だから,ローレンツ力とのつり合いを考えて
$\eqalign{eE&=ex\omega B\cr E&=x\omega B}$
だね.

それでは,縦軸を電場の大きさ$E$,横軸をPからの距離$x$としてグラフをかいてみましょう.
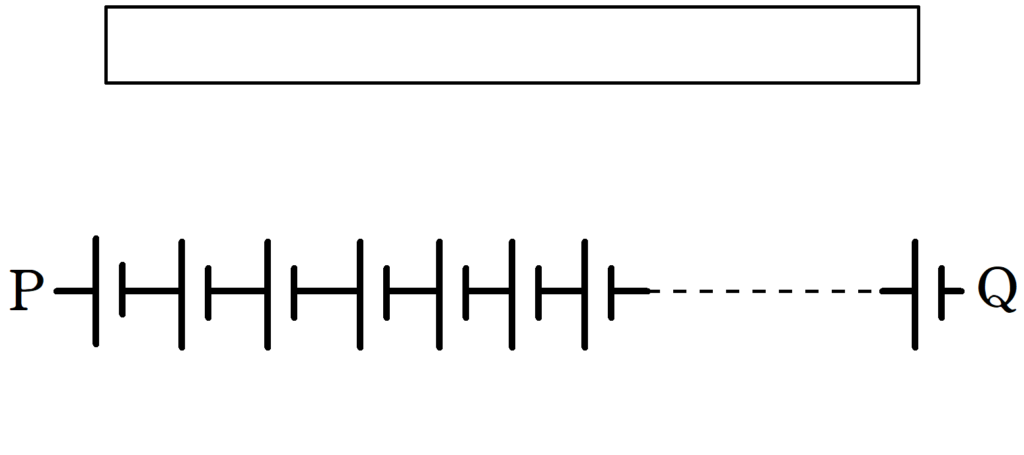
そして,下図のような長方形の面積を考えてみます.
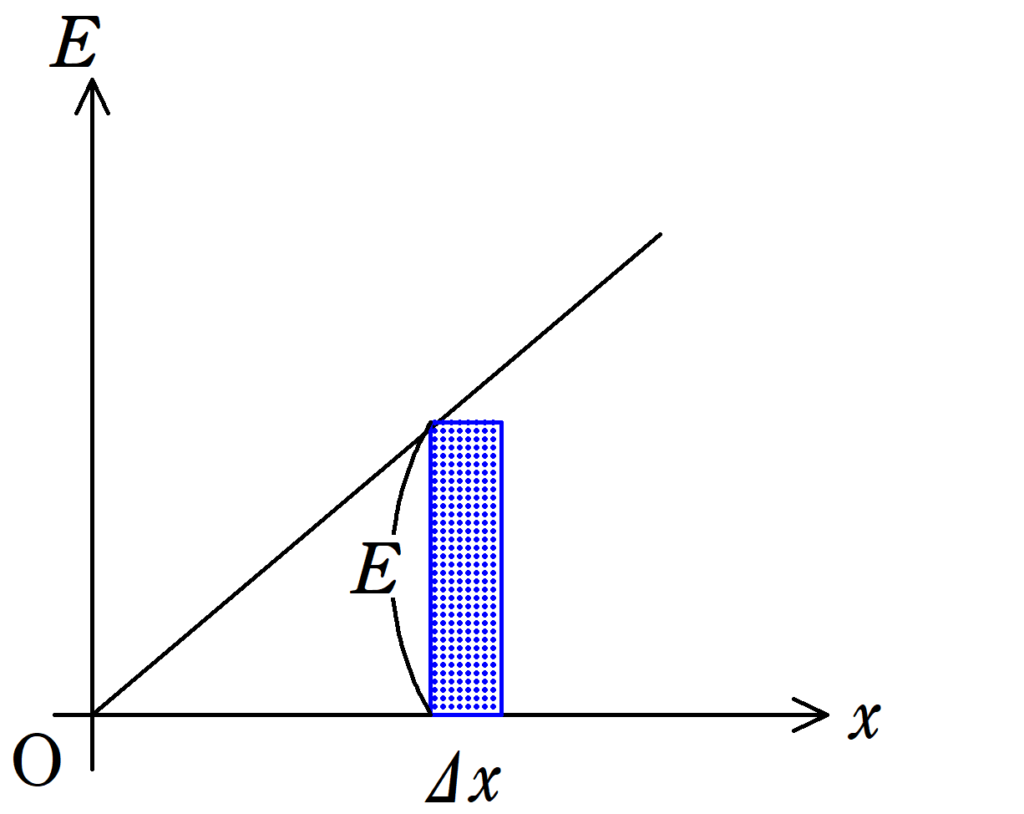

長方形の面積は$E\Delta x$だから,PQ間にある$\Delta x$部分の電位差を表しているね.この電位差を全部足し合わせればいいんだ.ってことは,次の三角形の面積を求めればいいだね!
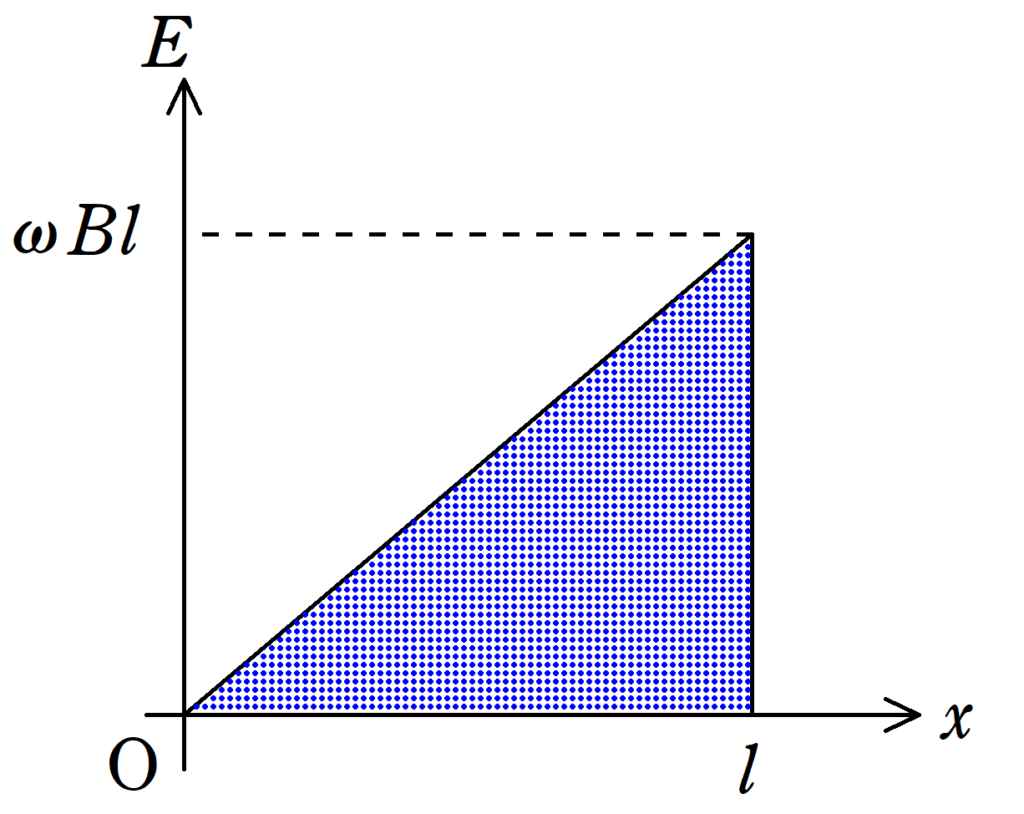

そういうことです.

面積は
$\dfrac{1}{2}\cdot l \cdot \omega Bl =\dfrac{1}{2}l^{2}\omega B$
だから,,本当だ!確かに$\dfrac{1}{2}$が出てきた.だからPQ間の誘導起電力が
$V=\dfrac{1}{2}l^{2}\omega B$
なんだ.

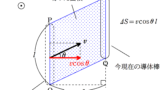
そして,この計算は,前回の扱ったような,導体棒が単位時間あたりに切る磁束を計算することでも計算できます.
導体棒PQの長さを$l$とする.導体棒が$\Delta t$の間に垂直に切った磁束を$\Delta \Phi$としたとき,誘導起電力の大きさ$V$は
$V=\dfrac{\Delta \Phi}{\Delta t}$
誘導起電力の向きは切った磁束と反対方向に右手の親指を向けたときの残りの4本指の向き.

そっか,PQ間の導体棒の各部分が切った磁束が誘導起電力になるから,結局,その和を求めると,導体棒全体が切り取った磁束を計算すればいいんだ!
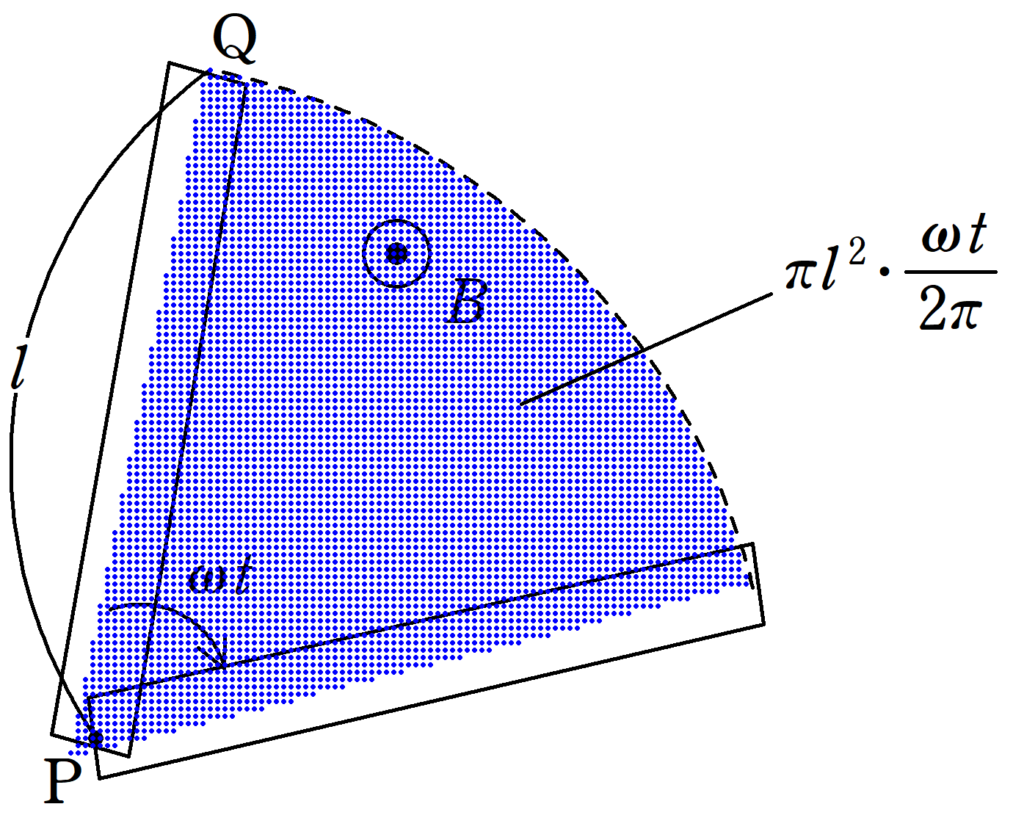

角速度が$\omega$のとき,時間$t$で$\omega t$だけ回転するので切り取った面積$S$は比を考えて
$S=\pi l^{2}\cdot \dfrac{\omega t}{2\pi}=\dfrac{1}{2}l^{2}\omega t$
だね.ちなみに比というのは
$\pi l^{2} : S=2\pi : \omega t$
のことだよ.だから誘導起電力の大きさ$V$は
$\eqalign{V&=\dfrac{\Delta \Phi}{\Delta t}\\&=\dfrac{B\Delta S}{\Delta t}\\&=\dfrac{B\Delta (\dfrac{1}{2}l^{2}\omega t)}{\Delta t}\\&=\dfrac{1}{2}l^{2}\omega B\cdot \dfrac{\Delta t}{\Delta t}\\&=\dfrac{1}{2}l^{2}\omega B}$
一緒になるね!しかも計算はこっちの方が楽かも.

では,演習問題で確認していきましょう.
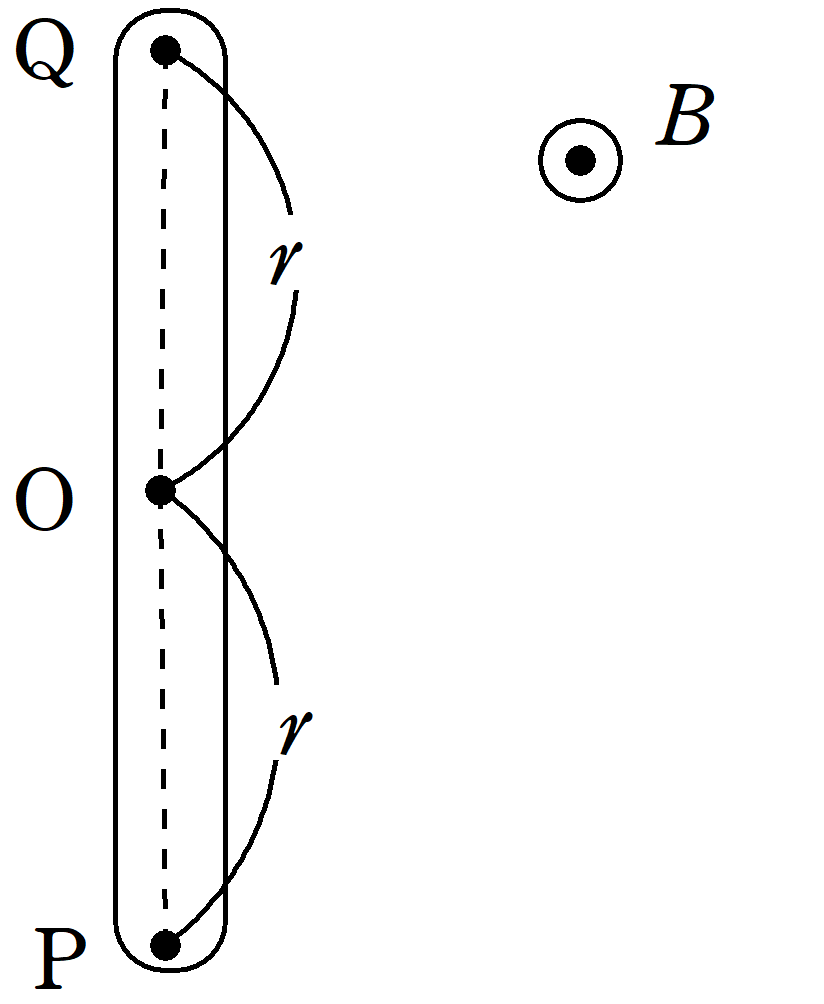
上図のように,画面裏から表に向かって一様な磁場がかけられていて,その磁束密度の大きさは$B$である.この磁場中に長さ$2r$の導体棒があり,導体棒の中心を$\rm{O}$,端を$\rm{P}$,$\rm{Q}$とする.このとき,次の問いに答えよ.
(1) $\rm{P}$を中心に導体棒を反時計回りに角速度$\omega$で回転させたときの$\rm{PQ}$間に生じる誘導起電力の大きさとその向きを答えよ.
(2) $\rm{O}$を中心に導体棒を時計回りに角速度$\omega$で回転させたときの,$\rm{OP}$間,$\rm{OQ}$間に生じる誘導起電力の大きさと向きを答えよ.また,$\rm{PQ}$間の電位差を答えよ.
<解答>
(1)
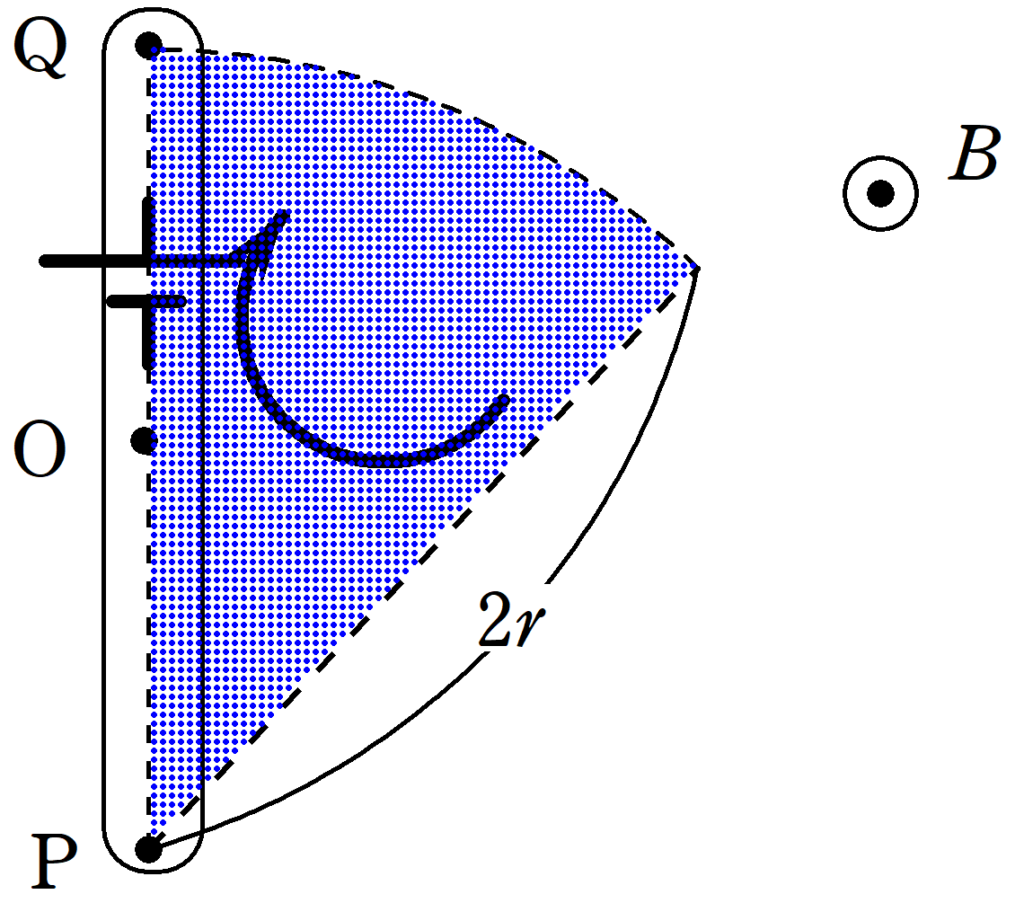
導体棒$\rm{PQ}$が磁束を切り取る面積$S$を求めます.時間$t$の間に導体棒は$\omega t$回転し,半径が$2r$なので
$\eqalign{S&=\pi \cdot (2r)^{2}\cdot \dfrac{\omega t}{2\pi}\\&=2r^{2}\omega t}$
したがって,誘導起電力の大きさ$V$は
$\eqalign{V&=\dfrac{\Delta \Phi}{\Delta t}\\&=\dfrac{B\Delta (2r^{2}\omega t)}{\Delta t}\\&=2r^{2}B\omega \dfrac{\Delta t}{\Delta t}\\&=2r^{2}B\omega}$
また,誘導起電力の向きは画面裏から表の磁場を切ったので,その反対方向である画面奥に親指を向けると,図のように$\rm{P}$から$\rm{Q}$の向きに誘導起電力が生じます.
したがって,$\rm{P}$から$\rm{Q}$の向きに大きさ$2r^{2}B\omega$
(2)
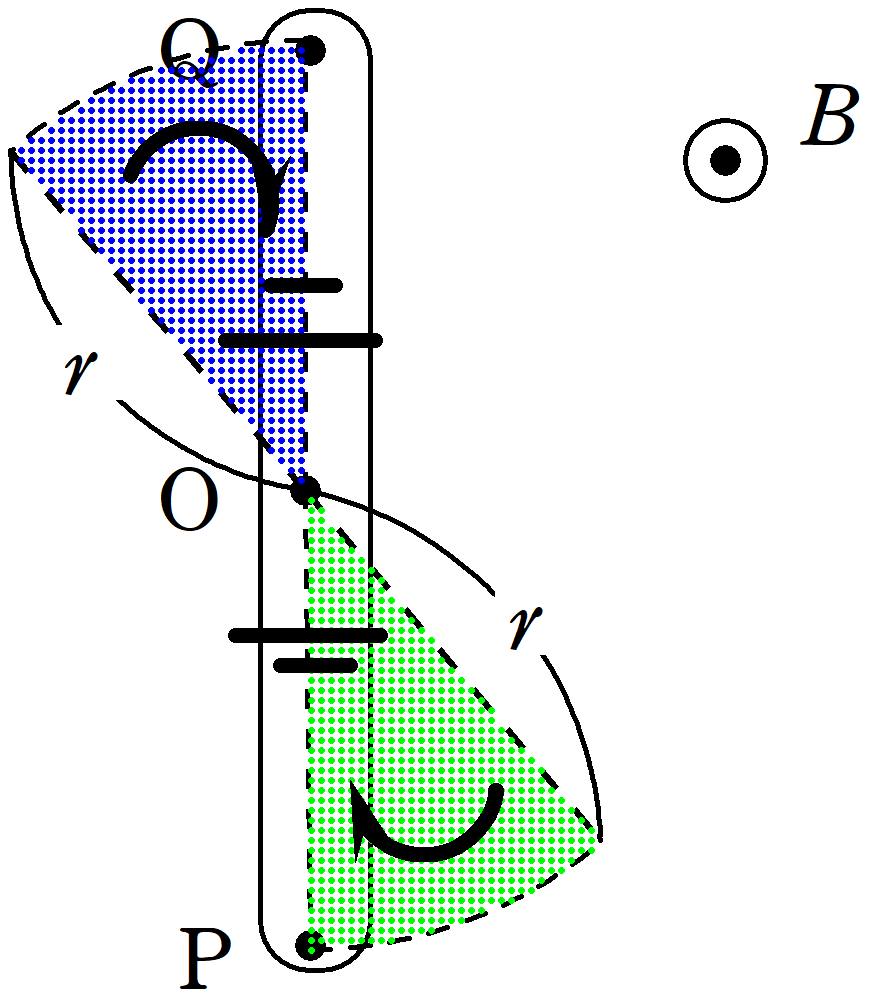
まずOP間に生じる起電力を計算しましょう.時間$t$の間に$\omega t$回転するので,磁束を切る面積(緑色部分)$S$は
$\eqalign{S&=\pi r^{2}\cdot \dfrac{\omega t}{2\pi}\\&=\dfrac{1}{2}r^{2}\omega t}$
したがって,誘導起電力の大きさ$V$は
$\eqalign{V&=\dfrac{\Delta \Phi}{\Delta t}\\&=\dfrac{B\Delta (\dfrac{1}{2}r^{2}\omega t)}{\Delta t}\\&=\dfrac{1}{2}r^{2}B\omega \dfrac{\Delta t}{\Delta t}\\&=\dfrac{1}{2}r^{2}B\omega}$
また,導体棒は画面裏から表向きの磁場を切り取ったので親指を反対方向である奥方向に向けると4本指は図のような向きを向く.したがって,誘導起電力の向きは$\rm{P}$から$\rm{O}$の向きになります.
同様に$\rm{OQ}$間も考えることができます.結論として
$\rm{OP}$間に生じる誘導起電力の大きさは$\dfrac{1}{2}r^{2}B\omega$,向きは$\rm{P}$から$\rm{O}$の向き.
$\rm{OQ}$間に生じる誘導起電力の大きさは$\dfrac{1}{2}r^{2}B\omega$,向きは$\rm{Q}$から$\rm{O}$の向き.
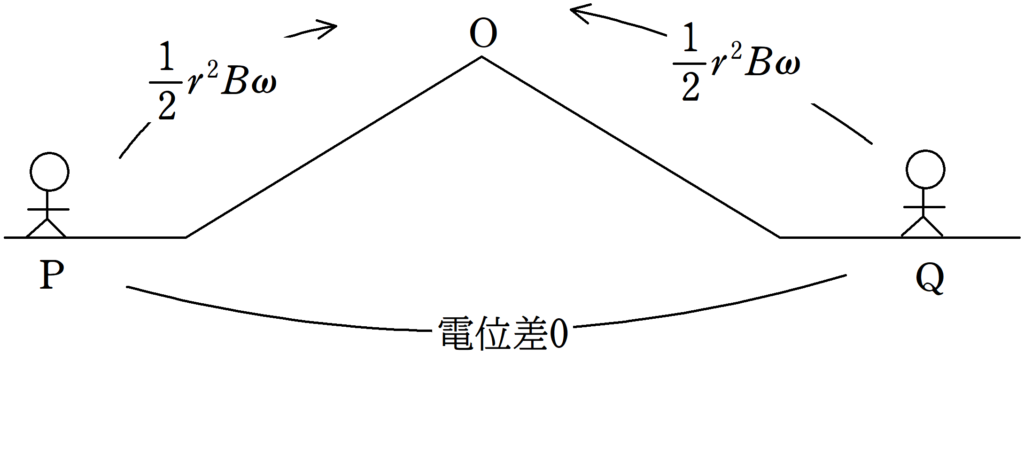
さて,$\rm{PQ}$間の電位差は$\dfrac{1}{2}r^{2}B\omega+\dfrac{1}{2}r^{2}B\omega$ということはしないようにしてくださいね.$\rm{P}$からみた$\rm{O}$の電位が$\dfrac{1}{2}r^{2}B\omega$,$\rm{Q}$からみた$\rm{O}$の電位が$\dfrac{1}{2}r^{2}B\omega$なので,PQの間の電位差は0です.下のイメージ図を参考にしてください.

これで回転している場合の導体棒の誘導起電力も計算ができるようになったね!次回はいよいよ回路の問題が出てきます.
次回の内容はこちら.



コメント
[…] […]
[…] […]
[…] 円運動 導体棒の磁場中の運動演習③[基本] | Physicmath(フィジクマス) より: 2021年2月10日 10:30 PM […]