
下図のように,起電力$V$の電池と電気容量$C$のコンデンサー,抵抗$R$をつないで,スイッチを閉じると,電池がした仕事の半分が静電エネルギーとして蓄えられて,もう半分が抵抗でジュール熱として消費されるんだよね??
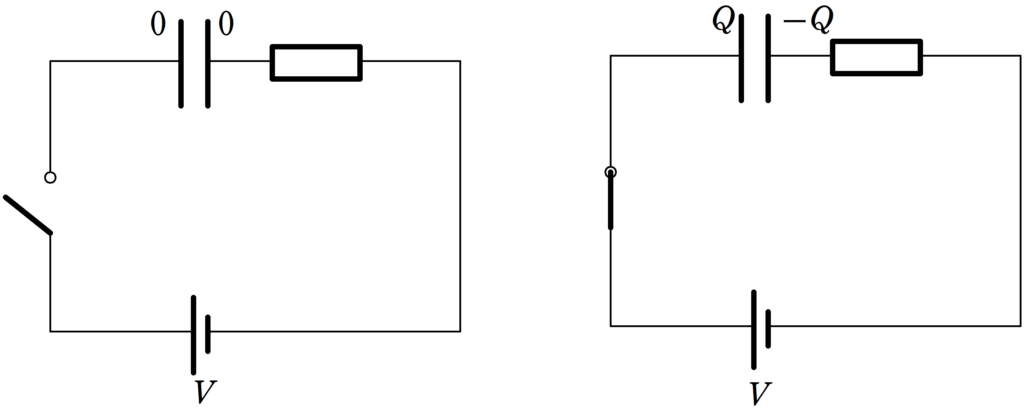

この場合はそうなりますね.
はじめ,コンデンサーに電荷が蓄えられていないとして,スイッチを閉じて十分時間が経った後のコンデンサーに蓄えられた電荷を$Q$とすると,電池がした仕事$W_{E}$は
$W_{E}=QV$
で,コンデンサーに蓄えられる静電エネルギー$U$は
$U=\dfrac{1}{2}QV$
なので,余ったエネルギー$\dfrac{1}{2}QV$が抵抗で消費されます.

もし抵抗がなかったらどうなるの?電池がした仕事がそのままコンデンサーの静電エネルギーになるの?

いえ,電池がした仕事と静電エネルギーは先ほどの値のままなので,別なエネルギーに変換すると考えられます.
抵抗が0に近いとコンデンサーの電荷を蓄えるスピードが速くなるので,短い時間の間にコンデンサー内に電場ができ,電場が生じることで磁場ができ,磁場が生じることで電場ができ,,,を続けてエネルギーを放出します.つまり,電磁波としてエネルギーを放出すると考えられています.

じゃあ,結局どんなときでも
電池がした仕事≠静電エネルギーの変化
となるわけだね.

いえ,そういうわけでもありません.たしかに,この手の問題は”電池がした仕事≠静電エネルギーの変化”のことが多いですが,もし,電池の起電力が一定ではなかったら,“電池がした仕事=静電エネルギーの変化”になることもあります.しかも,何気なくそのような問題も入試問題に出ています.

え?そうなの?たとえば,どういう問題のときに”電池がした仕事=静電エネルギーの変化”が成り立つの?

では,具体的に次の問題を考えてみましょう.
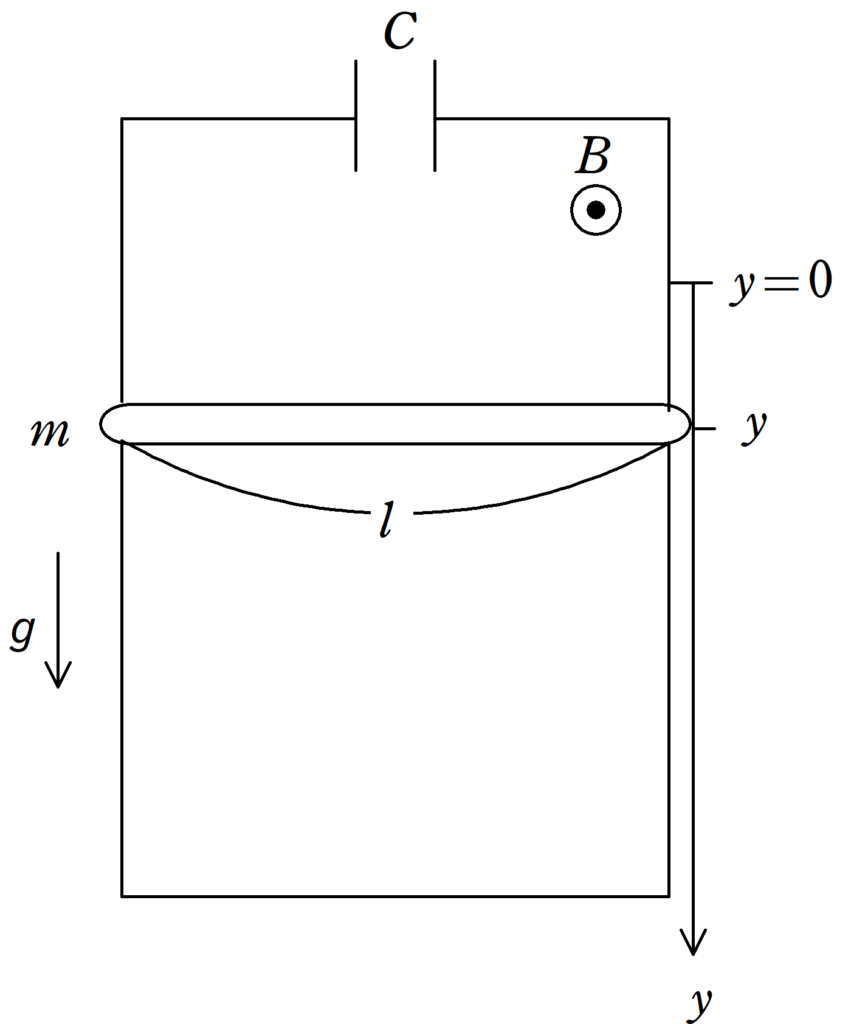
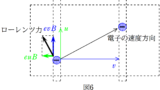
上図のように,画面裏から表の向きに一様な磁束密度$B$の磁場がかけられている.この磁場中に電気容量$C$で電荷が蓄えれていないコンデンサーと,質量$m$,長さ$l$の導体棒があり,コンデンサーと導体棒と導体レールで回路をつくる.回路は磁場を垂直に貫く向きにつくる.導体棒は導体レール上を鉛直方向に自由に動けるようになっている.時刻$t=0$で導体棒を静止させておき,静かに手をはなしてたところ,導体棒は導体レール上を離れずに運動を開始した.$t=0$での導体棒の位置を$y=0$として,鉛直下向きに$y$座標をとる.導体棒が$y=h$に達したときの速さを求めよ.ただし,重力加速度の大きさを$g$とし,導体棒と導体棒レールはなめらかであるとする.また,導体棒が受ける空気抵抗や回路の抵抗は無視をし,回路に流れる電流がつくる磁場の影響も無視をする.

導体棒が磁場中を運動すると,導体棒が電池になって回路に電流を流すね.だからコンデンサーに電荷が蓄えられるんだ.
速さを求めるには,エネルギー収支を考えればいいのかな?$y=-h$を重力による位置エネルギーの基準として,$y=0$での位置エネルギー$U_{g}=mgh$が導体棒の運動エネルギーとコンデンサーの静電エネルギーの和になると考えよう.$y=h$での導体棒の速さを$V$,蓄えられた電荷を$Q$とすれば
重力による位置エネルギー=運動エネルギー+静電エネルギー
だから
$mgh=\dfrac{1}{2}mV^{2}+\dfrac{Q^2}{2C}$
あれ,でも・・・・?

気づきましたか?この問題では,回路に着目すると,コンデンサーに静電エルギーが蓄えられた原因は導体棒に生じる誘導起電力が仕事をしたからなので,
電池(誘導起電力)がした仕事=静電エネルギー
となっています.
ちなみに,電磁力がした仕事と誘導起電力がした仕事の関係はこちらを参照してください.

本当だ,じゃあ間違っているのかな?

いえ,今回はこれでいんです.実際に確かめていましょう.
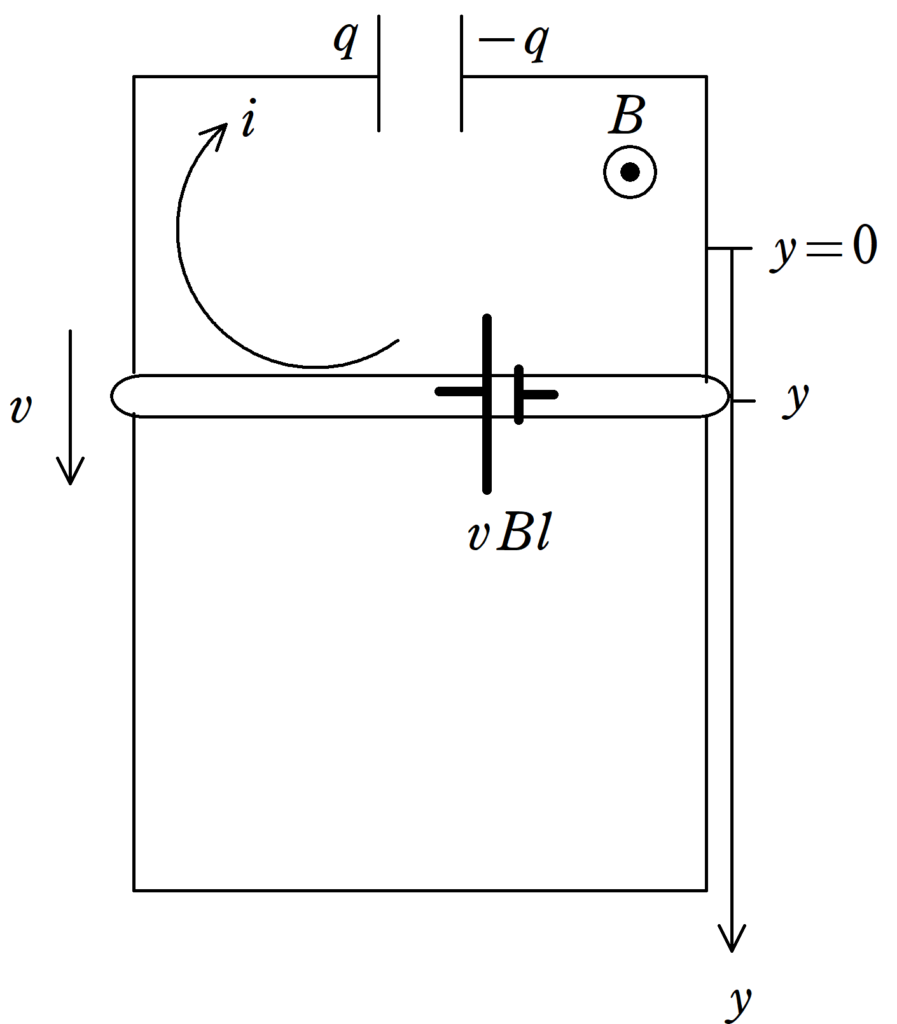
導体棒が$y=y$にいるときの速度を$v$とします.また,このとき,コンデンサーに蓄えられている電荷を$q$,回路に流れている電流を上図の向きに$i$としましょう.
磁場中に電流が流れているので,導体棒は電磁力$iBl$を$y$軸の負の向きに受けます.また,重力は$y$軸の正の方向に受けますね.導体棒の加速度を$y$軸の正の向きに$a$とすると,運動方程式は
$ma=mg-iBl$ $\dots (\ast)$
となります.また,電流$i$と$\Delta t$の間のコンデンサーの電荷の変化$\Delta q$の関係は
$i=\dfrac{\Delta q}{\Delta t}$ $\dots (2\ast)$
さらに,導体棒が速さ$v$で磁場中を動いているときに生じる起電力$E$は
$E=vBl$ $\dots (3\ast)$
コンデンサーの基本式に$(3\ast)$を代入して
$q=CE=CvBl$ $\dots (4\ast)$
$(4\ast)$を$(2\ast)$に代入して
$i=\dfrac{\Delta q}{\Delta t}=\dfrac{\Delta (CvBl)}{\Delta t}=CBl\dfrac{\Delta v}{\Delta t}$
加速度の定義式より,$a=\dfrac{\Delta v}{\Delta t}$を上式に代入して
$i=CBla$ $\dots (5\ast)$
$(5\ast)$を$(\ast)$に代入して
$\eqalign{ma&=mg-iBl\cr ma&=mg-CB^{2}l^{2}a\cr ma+CB^{2}l^{2}a&=mg\cr(m+CB^{2}l^{2})a&=mg\cr a&=\dfrac{mg}{m+CB^{2}l^{2}}}$
$a=\dfrac{mg}{m+CB^{2}l^{2}}$は時刻によらず一定なので等加速度運動をすることがわかります.すると,時刻$t$における導体棒の速度$v$は,等加速度運動の式より
$v=at=\dfrac{mg}{m+CB^{2}l^{2}}t$
なので,時刻$t$における導体棒に生じる誘導起電力の大きさ$E$は$(3\ast)$より
$E=vBl=\dfrac{mgBl}{m+CB^{2}l^{2}}t$ $\dots (6\ast)$
また,時刻$t$において,コンデンサーに蓄えられている電荷$q$は$(4\ast)$より
$q=CE=CvBl=\dfrac{mgCBl}{m+CB^{2}l^{2}}t$
さらに,$(2\ast)$より,時刻$t$における回路に流れる電流$i$は
$\eqalign{i&=\dfrac{\Delta q}{\Delta t}\\&=\dfrac{mgCBl}{m+CB^{2}l^{2}}\dfrac{\Delta t}{\Delta t}\\&=\dfrac{mgCBl}{m+CB^{2}l^{2}}}$ $\dots (7\ast)$
$(6\ast)$と$(7\ast)$より,単位時間あたりに誘導起電力がする仕事$P$は
$\eqalign{P&=iE\\&=\dfrac{mgCBl}{m+CB^{2}l^{2}}\cdot\dfrac{mgBl}{m+CB^{2}l^{2}}t \\&=\left(\dfrac{mgBl}{m+CB^{2}l^{2}}\right)^{2}Ct}$
このとき,縦軸を単位時間あたりに誘導起電力がした仕事$P$を,横軸に時刻$t$をとってグラフをかくと,次のようになります.
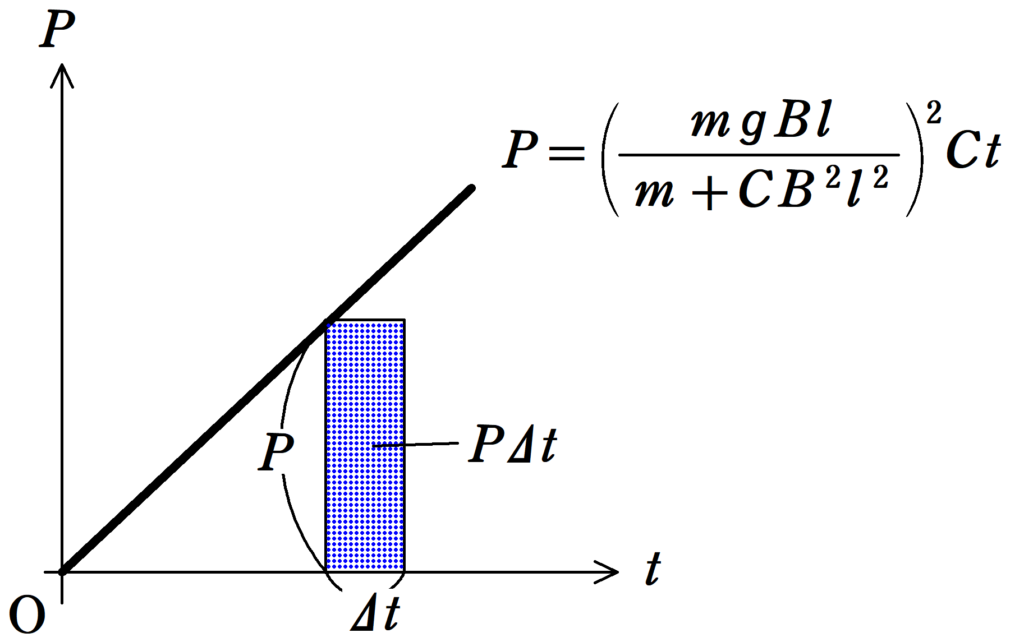
このとき,上図の長方形の面積が$P\Delta t$となり,$\Delta t$間の誘導起電力がした仕事を表しています.時刻によって変化するため,細かく足し合わせていきます.
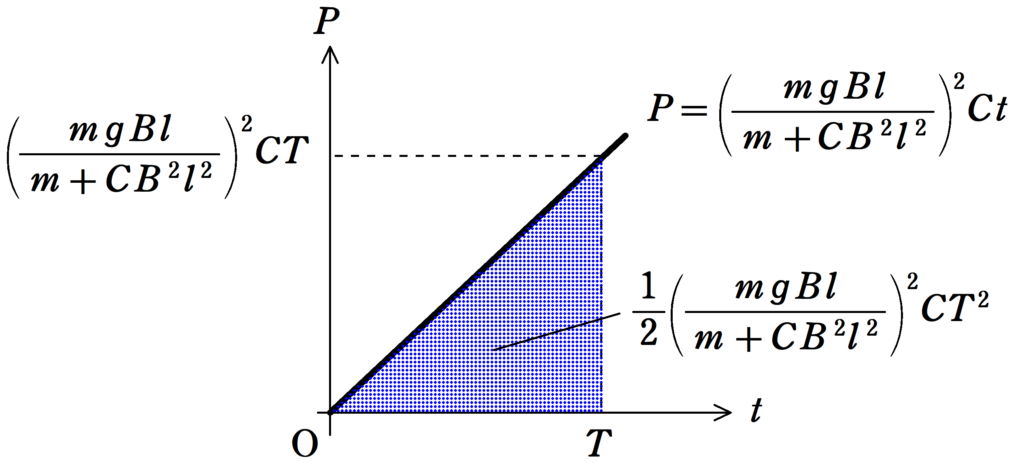
導体棒が$y=h$に達したときの時刻を$t=T$とすると,$t=0$から$t=T$までに誘導起電力がした仕事$W$は上図の青色の三角形の面積を求めて,
$\eqalign{W&=\dfrac{1}{2}T\cdot \left(\dfrac{mgBl}{m+CB^{2}l^{2}}\right)^{2}CT\\&=\dfrac{1}{2}\left(\dfrac{mgBl}{m+CB^{2}l^{2}}\right)^{2}CT^2}$ $\dots (\clubsuit)$
次に,$t=T$を$(6\ast)$に代入すると,$E=\dfrac{mgBl}{m+CB^{2}l^{2}}T$であるから,$t=T$でコンデンサーに蓄えらえた静電エネルギー$U$は
$\eqalign{U&=\dfrac{1}{2}CE^2\\&=\dfrac{1}{2}\left(\dfrac{mgBl}{m+CB^{2}l^{2}}\right)^{2}CT^2}$ $\dots (\heartsuit)$

$(\clubsuit)$と$(\heartsuit)$が同じになったね!つまり
電池がした仕事=静電エネルギーの変化
になってる!(計算は大変だったけど・・)

では,
$mgh=\dfrac{1}{2}mV^{2}+\dfrac{Q^2}{2C}$
の式を使って$y=h$のときの導体棒の速さ$V$を求めましょう.(等加速度運動の式から求めてもよいです.)先ほど,$t=T$における誘導起電力$E$を計算したので上式は
$mgh=\dfrac{1}{2}mV^{2}+\dfrac{1}{2}CE^2$
としましょう.
$E=VBl$より
$\eqalign{mgh&=\dfrac{1}{2}mV^{2}+\dfrac{1}{2}CE^2\cr \dfrac{1}{2}mV^{2}+\dfrac{1}{2}C(VBl)^2 &=mgh\cr \dfrac{1}{2}(m+CB^{2}l^{2})V^2&=mgh \cr V^2&=\dfrac{2mgh}{m+CB^{2}l^{2}}\cr V&=\sqrt{\dfrac{2mgh}{m+CB^{2}l^{2}}}}$

答えは,$V=\sqrt{\dfrac{2mgh}{m+CB^{2}l^{2}}}$だね.
でも入試で出たら,ここまで考察する時間はないかも・・.

物理の問題はヒントをかいてくれることもありますし,問題文をよく読んで問題に答えるようにしましょう.


コメント
[…] 電池がした仕事≠静電エネルギーの変化?NEKO下図のように,起電力$V$の電… […]
[…] 電池がした仕事≠静電エネルギーの変化? […]