
前回は,導体棒が磁場中を動くことで起電力が生じる(電池になる)という話をしました.今回は,ファラデーの電磁誘導の法則の形を利用して演習問題を解いてみます.
前回の内容はこちら
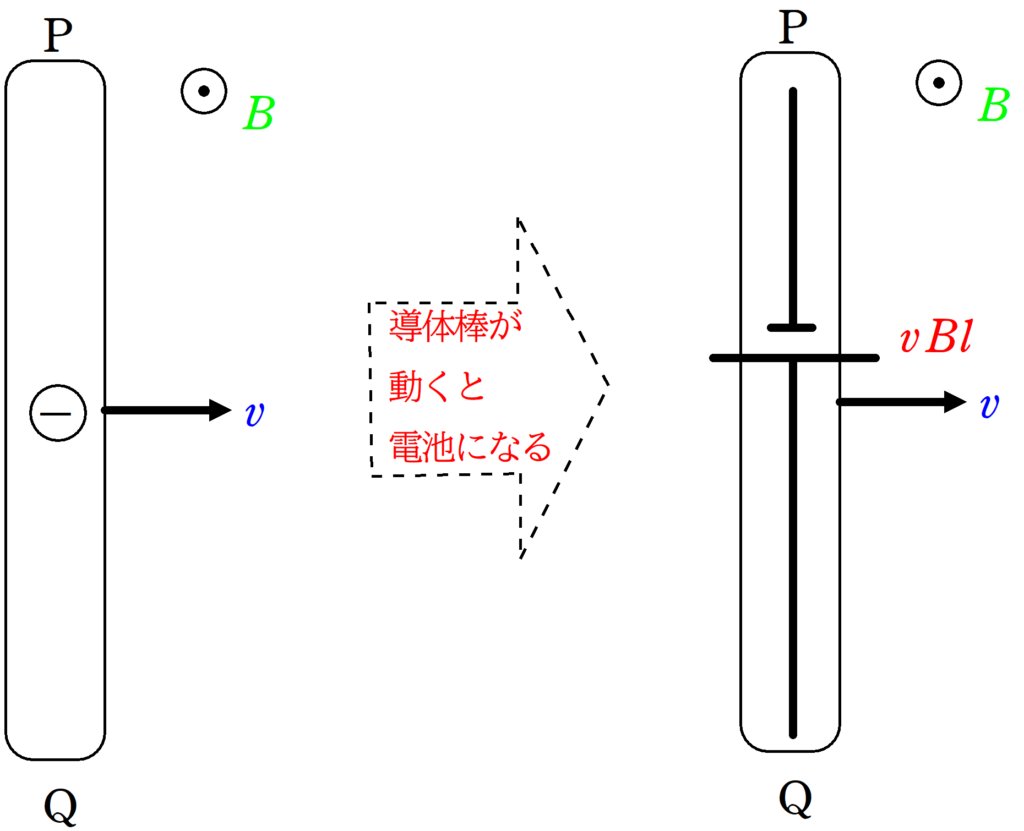

前回はローレンツ力を用いて誘導起電力の大きさを求めました.
$V=vBl$
ですね.これを次のように式変形してみましょう.
$\eqalign{V&=vBl\\&=\dfrac{v\Delta t Bl}{\Delta t}\\&=\dfrac{(v\Delta t l)B}{\Delta t}\\&=\dfrac{B\Delta S}{\Delta t}=\dfrac{\Delta \Phi}{\Delta t}}$

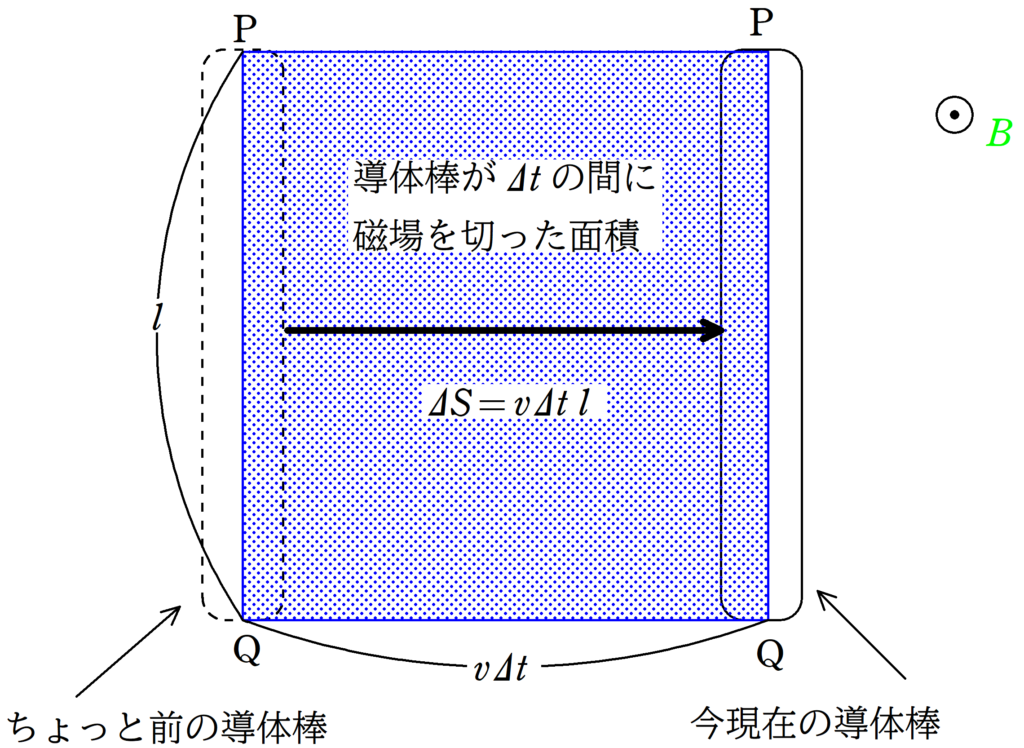
上の式で$\Delta S$は導体棒が時間$\Delta t$の間に磁場を垂直に切り取る面積です.また,$\Delta \Phi$は$\Delta t$の間に導体棒が垂直に切り取った磁束です.

導体棒が磁束を切り取っていくイメージなんだね.
誘導起電力の向きはどうやって決めるの?

上の導体棒は左から右へ動いていて,画面裏から表の磁束を切っていますね.この切り取った磁束と反対方向に磁場をつくるような向きに起電力が生じます.右ねじの法則を思い出しましょう.
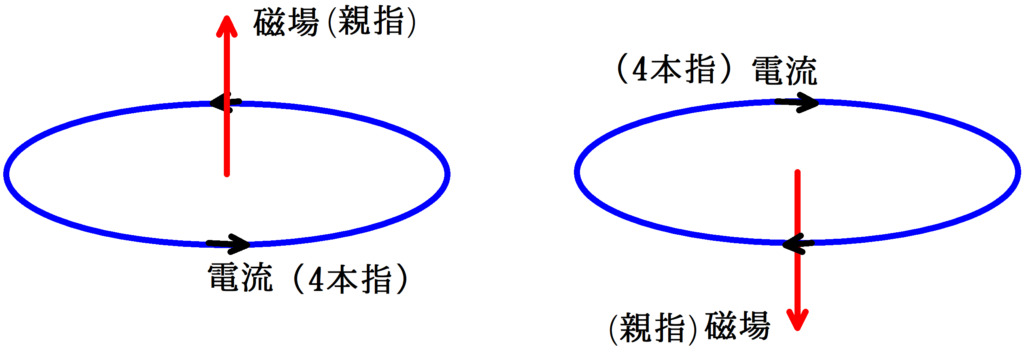

円電流のときに出てきたね.
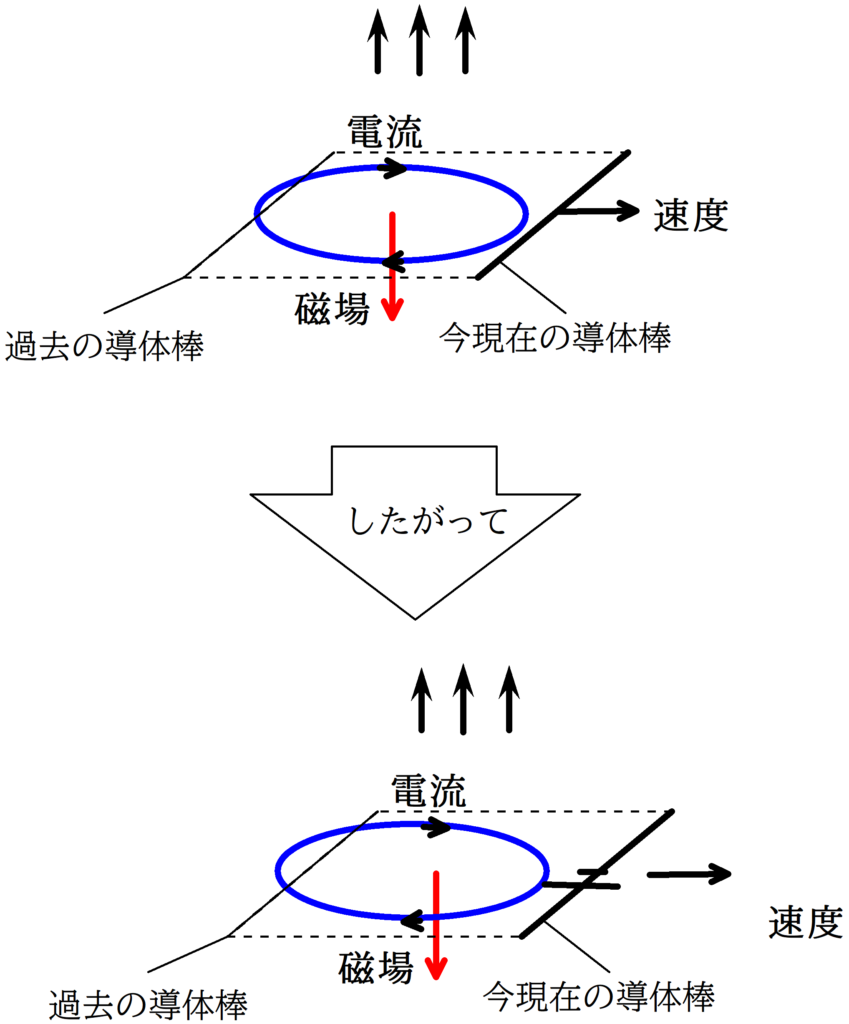

なるほど,導体棒が切り取った磁束と反対方向に右手の親指を向けて,4本指が向く方向が起電力の向きなんだ.

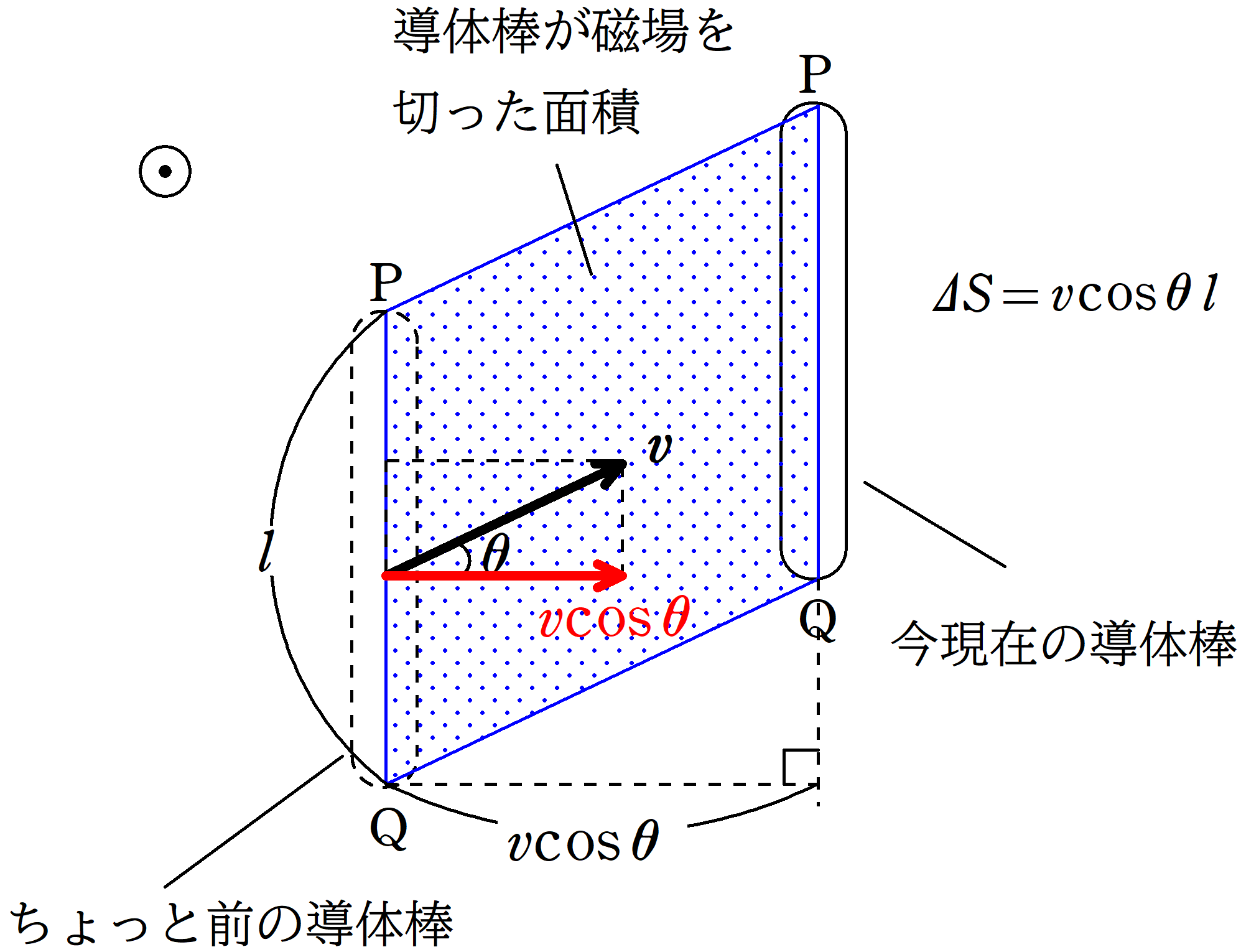
はい,そして$V=\dfrac{\Delta \Phi}{\Delta t}$は次のように,導体棒速度が長さ方向に垂直でないときでも使えます.
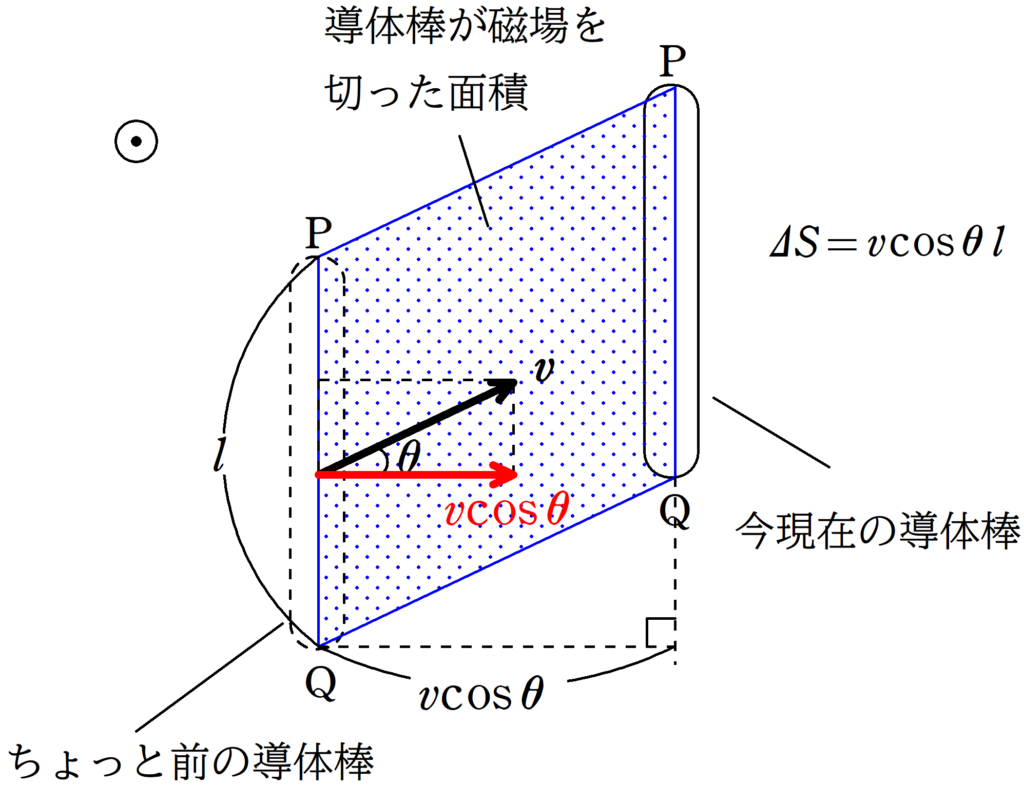

$\Delta t$の間に導体棒が切り取った面積は上図の青色部分だね.青色部分は平行四辺形だから$\Delta t$の間に切り取った面積$\Delta S$は
$\Delta S=l\cdot v\cos \theta \Delta t$
だね.だから
$\eqalign{V&=\dfrac{\Delta \Phi}{\Delta t}\\&=\dfrac{B\Delta S}{\Delta t}\\&=\dfrac{Bl\cdot v\cos \theta \Delta t}{\Delta t}\\&=vBl\cos \theta}$
これは前回やった,”導体棒に生じる起電力の式”
$V=v_{\perp}Bl$ $\dots (\clubsuit)$
と一致するね.

でも正直,$(\clubsuit)$を覚えてしまった方が楽だと思うだけど・・・

たしかに,今回の問題であれば$(\clubsuit)$を使った方が楽ですね.しかし,$(\clubsuit)$の式では計算が面倒なこともあるんです.これは次回扱います.

どっちも使えた方がいいだね!
じゃあ演習問題をやってみよう!
図のように,導体棒が動いたときにPQ間に生じる起電力の大きさと向きを$V=\dfrac{\Delta \Phi}{\Delta t}$を利用して計算せよ.ただし,導体棒PQの長さは$l$であり,磁束密度の大きさを$B$とする.
(1)
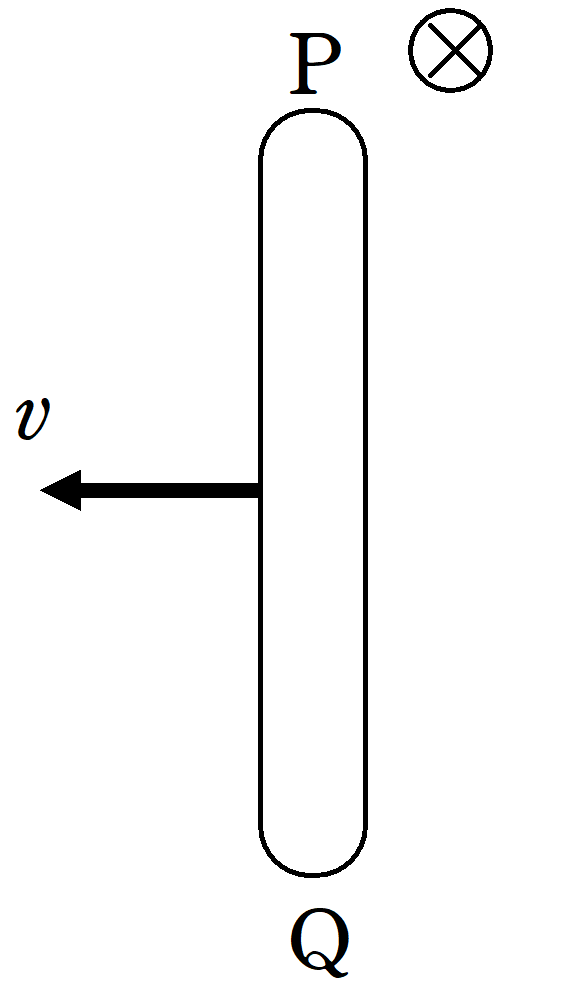
(2)

<解答>
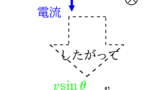
(1)
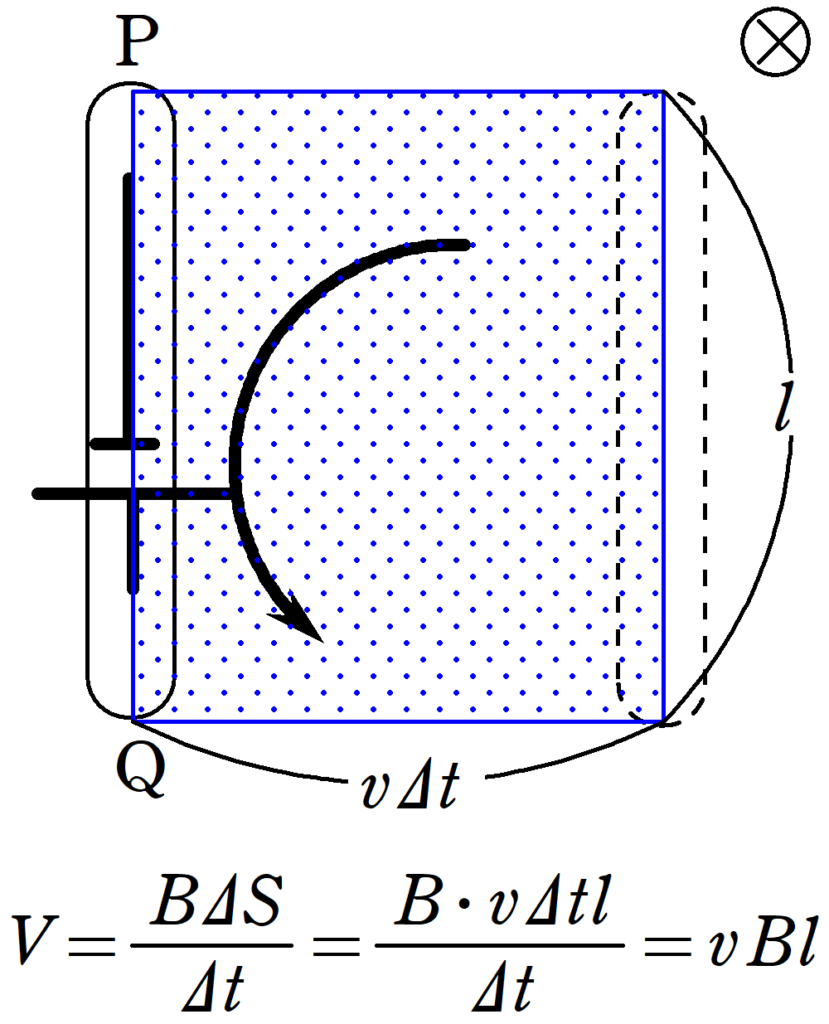
$\Delta S=v\Delta t l$より
$\eqalign{V&=\dfrac{\Delta \Phi}{\Delta t}\\&=\dfrac{B\Delta S}{\Delta t}\\&=\dfrac{Bv\Delta t l}{\Delta t}=vBl}$
したがって,$V=vBl$.また,導体棒は画面手前から奥方向の磁束を切っているので,親指を手前方向に向けると4本指は図のような向きとなります.だから,起電力の向きはPからQの方向となります.
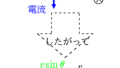
(2)
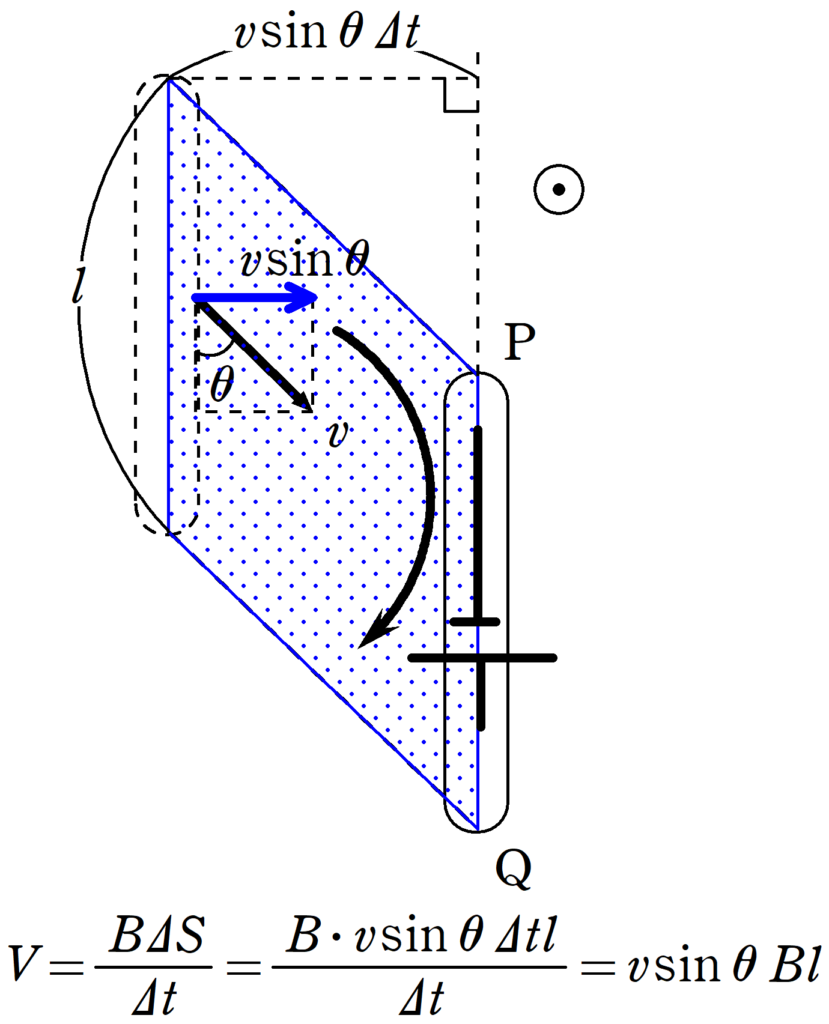
$\Delta S=v\sin \theta\Delta t l$より
$\eqalign{V&=\dfrac{\Delta \Phi}{\Delta t}\\&=\dfrac{B\Delta S}{\Delta t}\\&=\dfrac{Bv\sin \theta \Delta t l}{\Delta t}=v\sin \theta Bl}$
したがって,$V=v\sin \theta Bl$.また,導体棒は画面奥から手前方向の磁束を切っているので,親指を奥方向に向けると4本指は図のような向きとなります.だから,起電力の向きはPからQの方向となります.
導体棒PQの長さを$l$とする.導体棒が$\Delta t$の間に垂直に切った磁束を$\Delta \Phi$としたとき,誘導起電力の大きさ$V$は
$V=\dfrac{\Delta \Phi}{\Delta t}$
誘導起電力の向きは切った磁束と反対方向に右手の親指を向けたときの残りの4本指の向き.

今回はこれでおしまいです!
次回の内容はこちら.


コメント
[…] […]
[…] […]
[…] […]