導体棒が磁場中を動くことで生じる起電力

導体棒が磁場中を運動する問題はいろいろなことが聞かれるから難しい...
試験にはよく出るから演習をしないと.

そうですね.確かにいろいろな要素が混ざって複雑に感じるかもしれません.
では,一つ一つ確認しながら演習しましょう.
まずは,導体棒が磁場の向きに垂直に横切ると誘導起電力が生じるという話からしましょう.

電池になるんだよね.どんな仕組みなんだっけ?

観測者を静止している人としましょう.導体棒が磁場中を動くということは,導体棒の中にある自由電子も一緒に動いていますね.

そうか,自由電子が磁場中を動くとローレンツ力を受けるんだ.例えば,下図のように導体棒の中にある自由電子は赤矢印の向きにローレンツ力を受けるね.
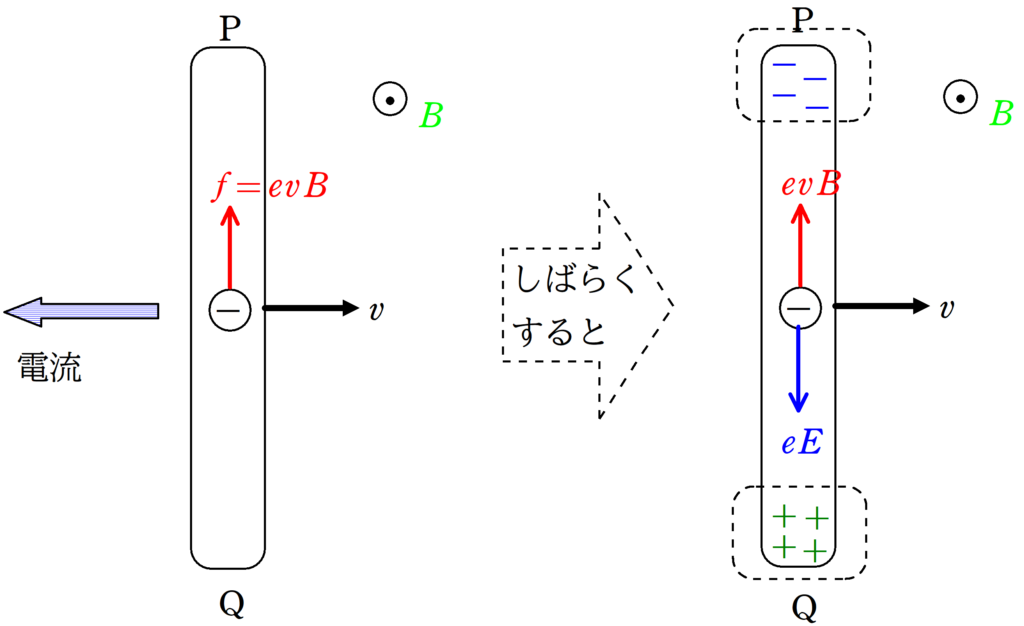

そうです.自由電子が上図右方向に動いているので,電流が左方向に流れているとも言えます.フレミング左手の法則でローレンツ力の向きがわかりますね.頭の中で$xyz$座標を描いてもいいです.
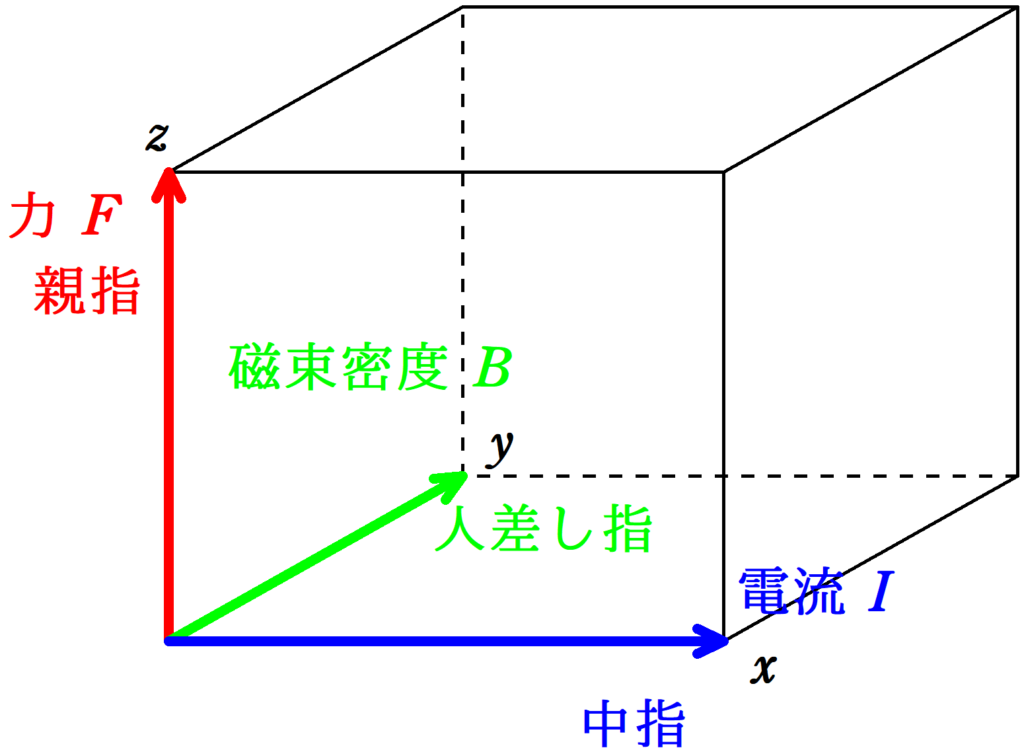
フレミング左手の法則

すると,Pの方に電子が集まって,Qの方は正電荷が取り残されるんだ.
たしか,正電荷と負電荷が分かれたことで電場をつくるんだね.

そうです.電荷が分かれていくことで電場もだんだんと大きくなります.
電場中に電荷があるとクーロン力を受けます.やがて,クーロン力とローレンツ力がつり合います.自由電子の電荷を$-e$,電場の大きさを$E$,磁束密度の大きさを$B$,導体棒の速さを$v$とすると次の関係式が成り立ちます.
$eE=evB$ $\therefore E=vB$ $\dots (\ast)$

電場が生じているので,導体棒PQの間は電位差があります.導体棒P,Qの間の電位差を$V$,導体棒PQの長さを$l$とすると
$V=El=vBl$ $\dots (2\ast)$

$(2\ast)$を導く計算の途中で$(\ast)$を使ったね.
導体棒を磁場中で動かすとできる電池の起電力は速さと磁束密度と長さで決まるんだね!そして,導体棒に生じる起電力はローレンツ力がはたらく向きと反対方向なんだ.
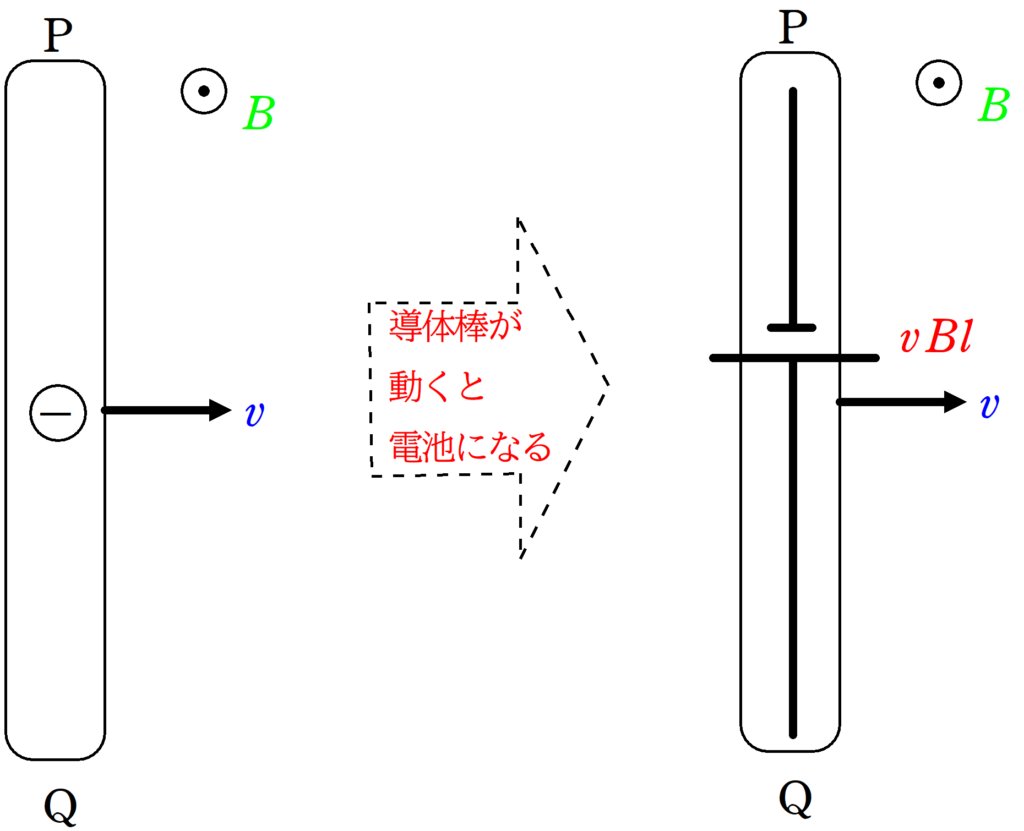
導体棒が斜め方向に動いたときに生じる起電力

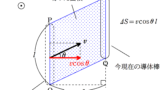
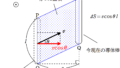
もし,導体棒が次のように斜めに動いていたらどうなるの??
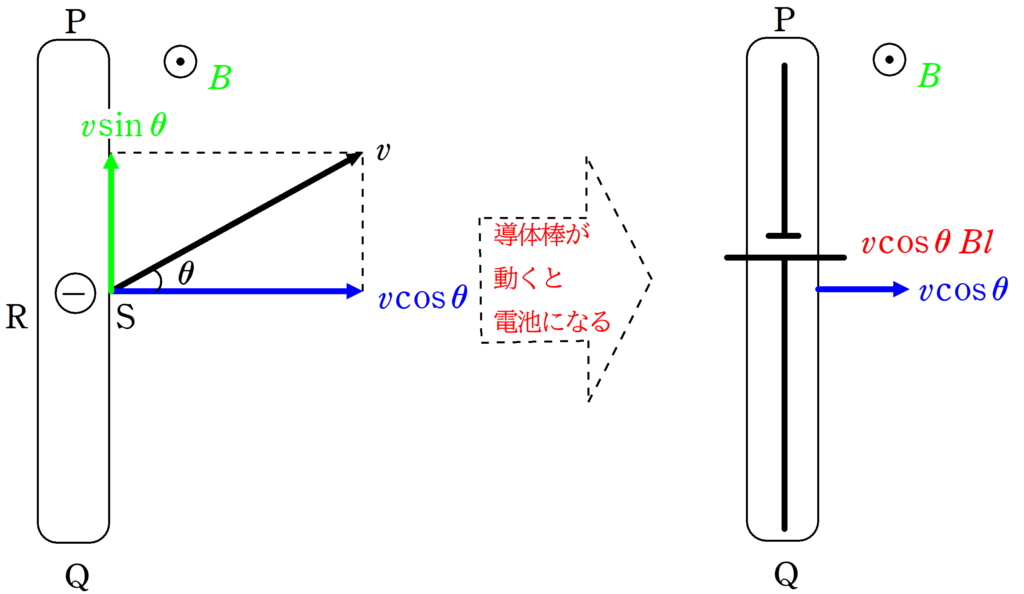

PQ間に生じる起電力はPQに対して垂直な速度成分のみ使います.上図では,$v\cos \theta$の成分ですね.だから,PQ間に生じる起電力$V_{\rm{PQ}}$は
$V_{\rm{PQ}}=v\cos \theta Bl$
となります.

じゃあ,PQ方向の速度成分は全く関係ないの?

PQ間に生じる起電力には関係ありません.$v\sin \theta$の速度成分はRS間に生じる起電力と関係します.問題で出てくることはあまりありませんが.
PQ間に生じる誘導起電力の大きさ$V_{\rm{PQ}}$は,PQの長さを$l$,PQ方向に垂直な速さを$v_{\perp}$,導体棒が動く方向と垂直な磁束密度の大きさを$B$とすれば,
$V=v_{\perp}Bl$

よし,これを使って演習問題を解いてみよう.
演習問題
次の導体棒PQに生じるPQ間の誘導起電力の大きさを求めよ.ただし,導体棒PQの長さを$l$,磁束密度の大きさを$B$とする.また,誘導起電力の向きを答えよ.(誘導起電力の向きは電位が低い方から高い方向を指す)
(1)
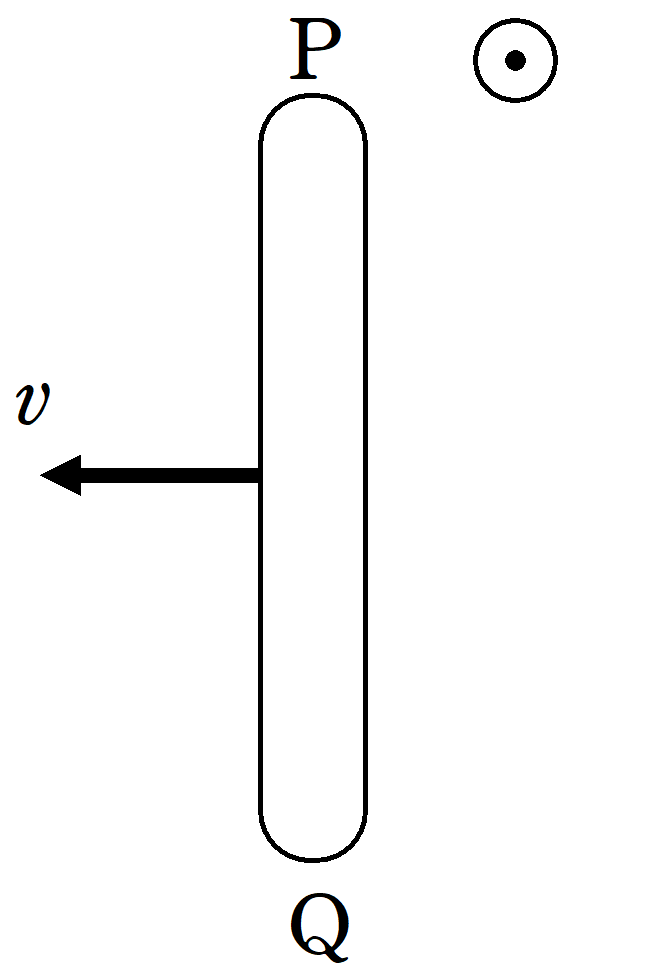
(2)
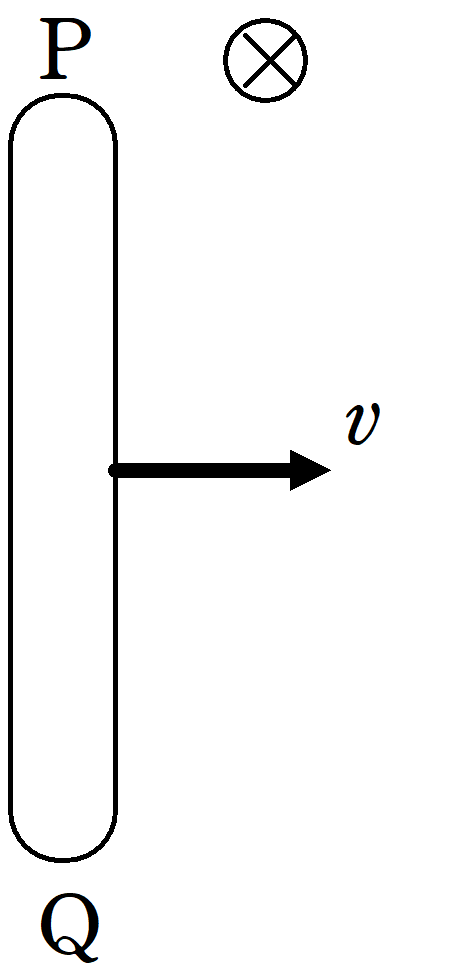
(3)

(4)
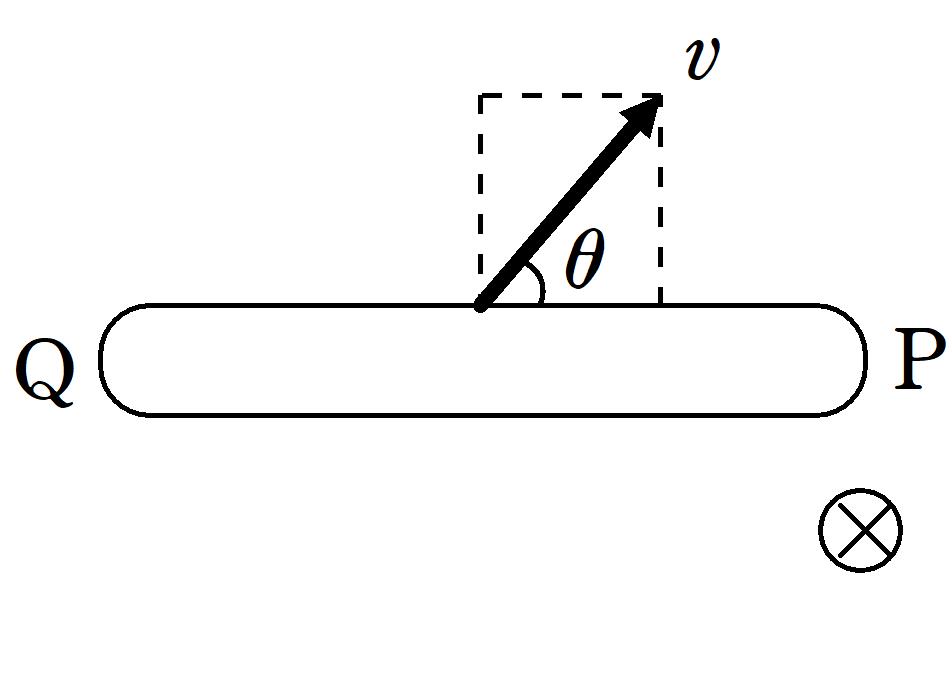
<解答>
(1)
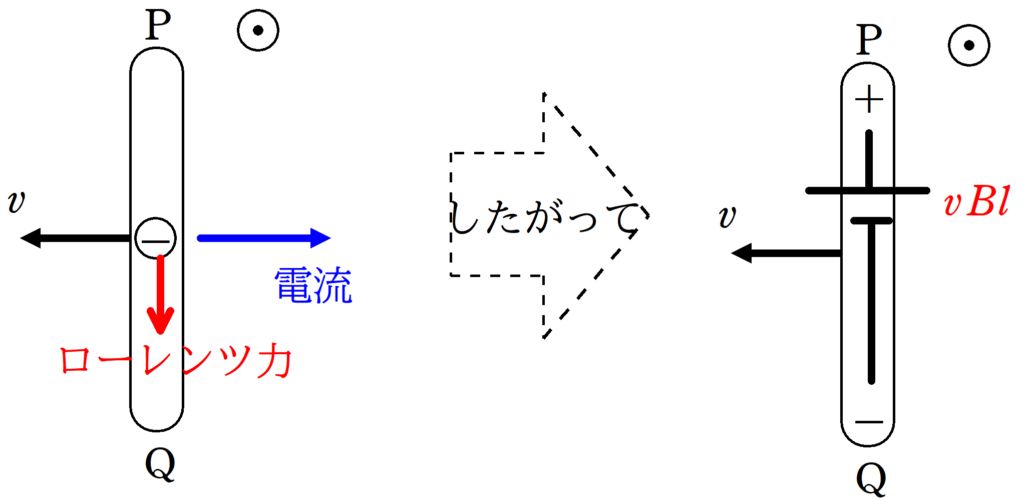
導体棒が左方向に動く→自由電子が左方向に動く→電流が右に流れる→自由電子がローレンツ力を下向きに受ける
したがって,P側に+,Q側に-がたまるので,誘導起電力の向きはQ→Pです.その大きさは$vBl$.
(2)
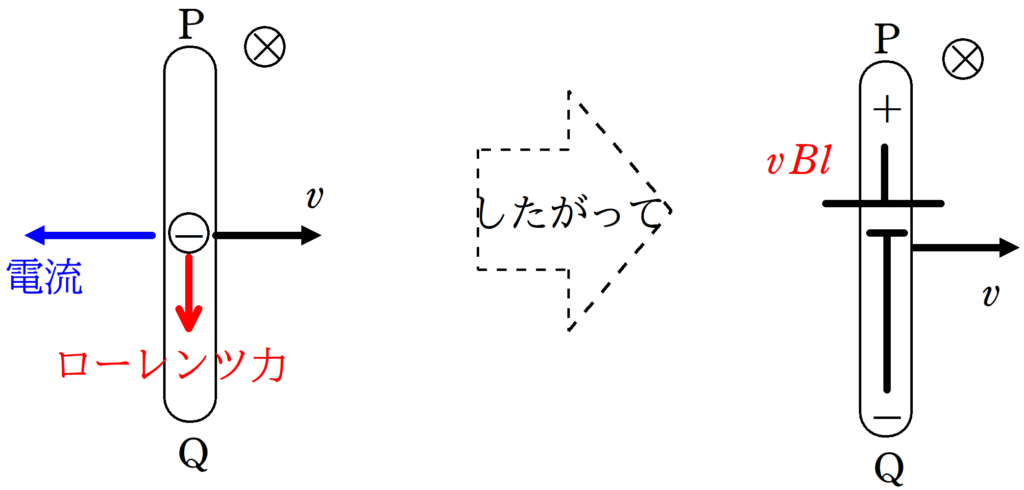
導体棒が右方向に動く→自由電子が右方向に動く→電流が左に流れる→自由電子がローレンツ力を下向きに受ける
したがって,P側に+,Q側に-がたまるので,誘導起電力の向きはQ→Pです.その大きさは$vBl$
(3)
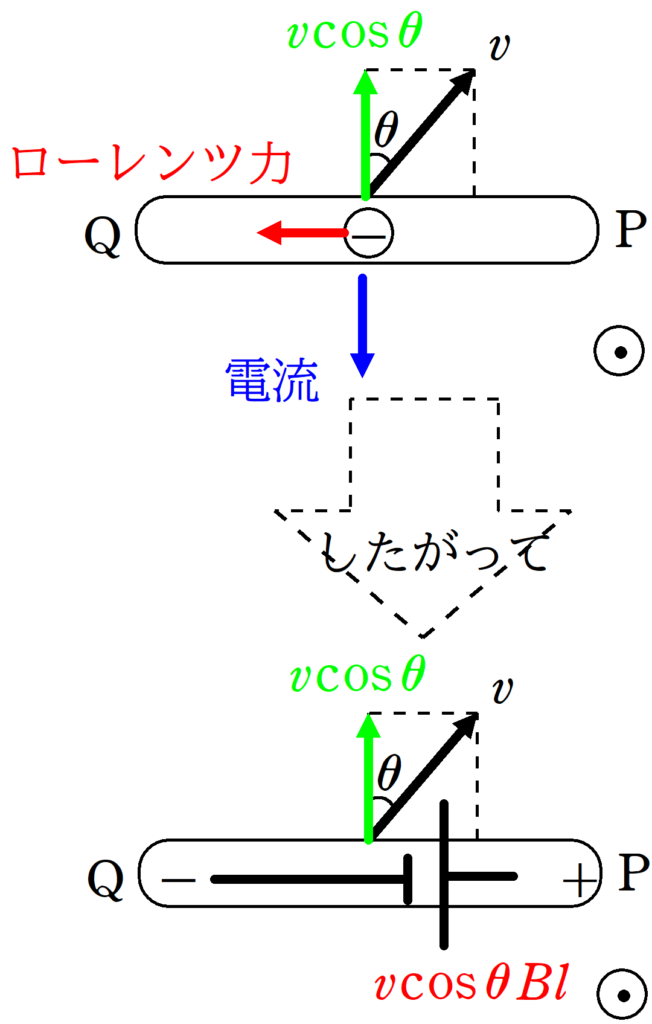
導体棒が上方向(速さ$v\cos \theta)$に動く→自由電子が上方向に動く→電流が下に流れる→自由電子がローレンツ力を左向きに受ける
したがって,P側に+,Q側に-がたまるので,誘導起電力の向きはQ→Pです.その大きさは$v\cos \theta Bl$
(4)
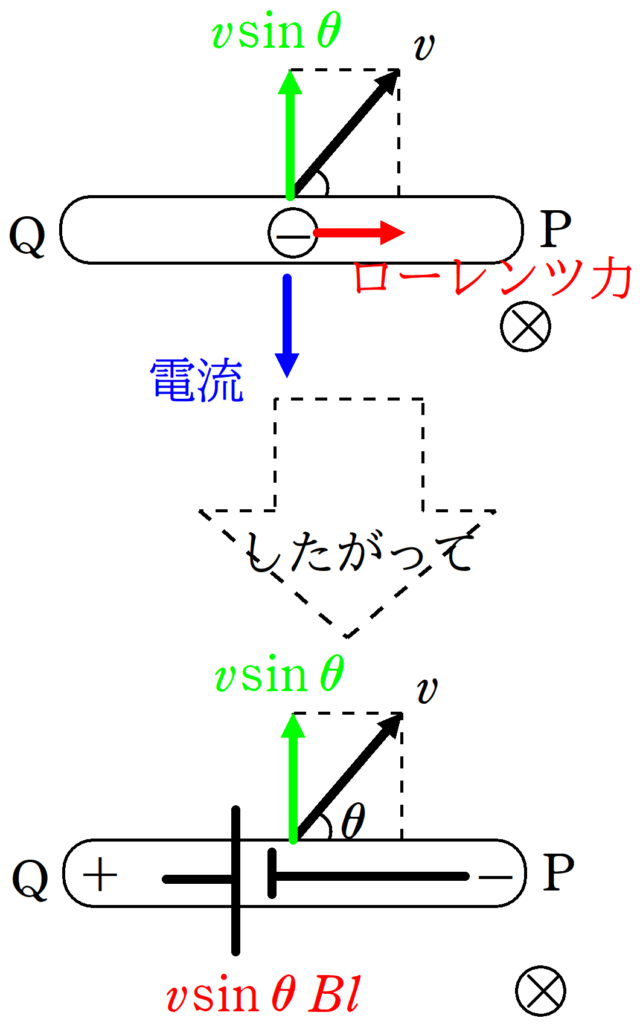
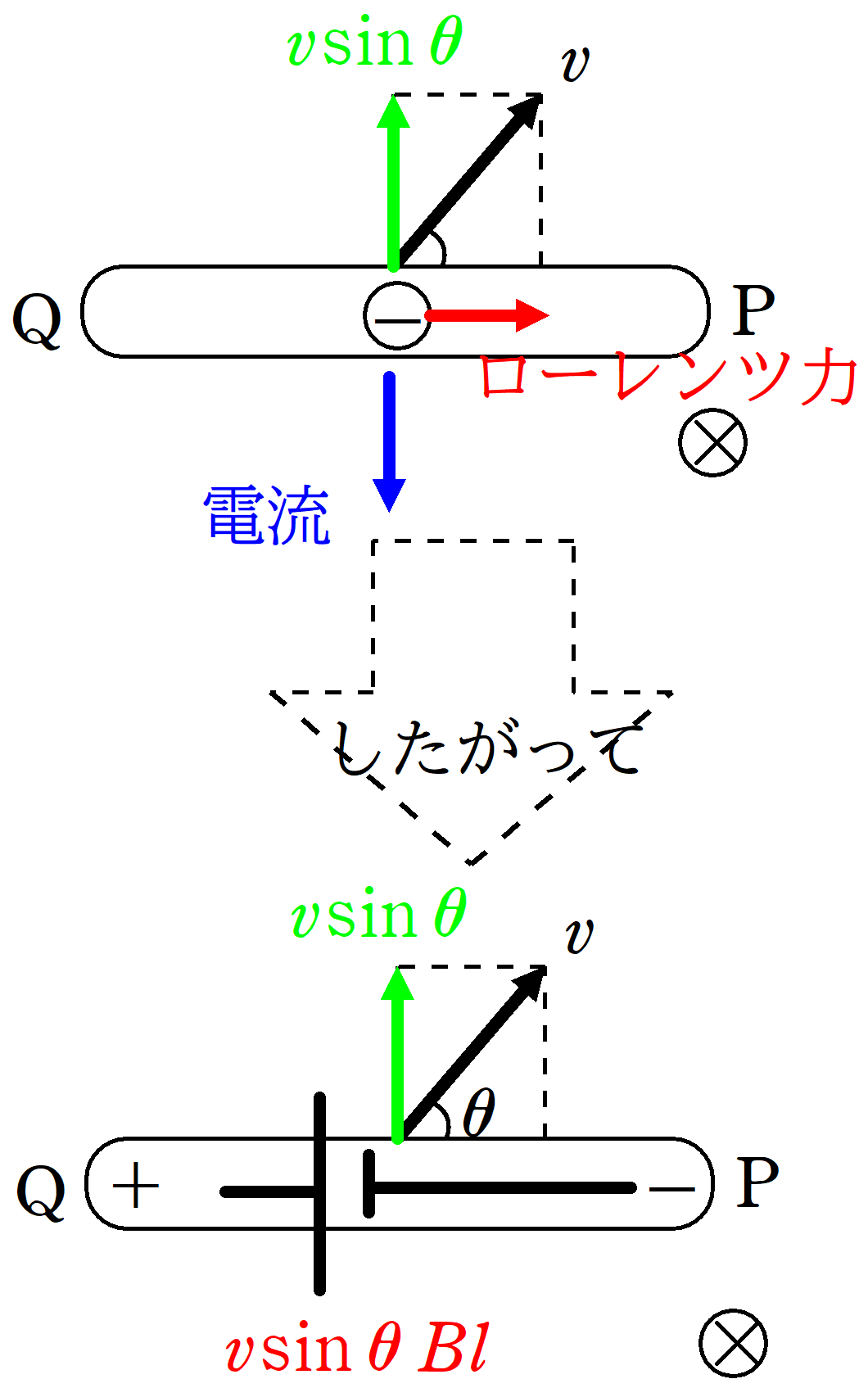
導体棒が上方向(速さ$v\sin \theta)$に動く→自由電子が上方向に動く→電流が下に流れる→自由電子がローレンツ力を右向きに受ける
したがって,Q側に+,P側に-がたまるので,誘導起電力の向きはP→Qです.その大きさは$v\sin \theta Bl$

導体棒が磁場中を動くときに電池になる!
そのときに大事なのは次の2つです.
- 起電力の向き(マイナス側からプラス側の向き)
- 起電力の大きさ
次回は別な計算で導体棒の誘導起電力を求めてみましょう.
次回の内容はこちら.


コメント
[…] […]
[…] […]
[…] […]
[…] […]