
今回は,コンデンサーの直列合成と並列合成について扱います.
合成の式は,ただ単に覚えるだけではだめです.
その使用条件の確認,そして,どのようなときに使う傾向があるのか,どのような問題のときは避けた方がいいのかについても知っておくとよいでしょう.
それでは,まずは,合成容量の式の確認です.
1.直列合成
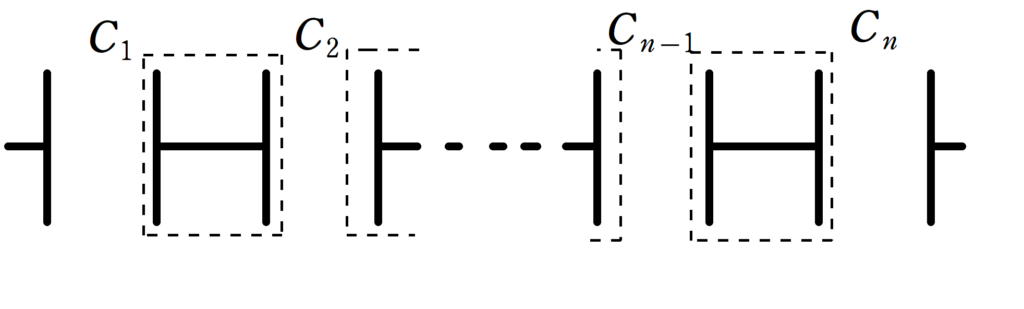
電気容量$C_{1}$,$C_{2}$,$\dots$,$C_{n-1}$,$C_{n}$の$n$個のコンデンサーを直列に結ぶ.
上図のように,点線で囲まれた各部分の電荷の和が0のとき,この$n$個のコンデンサーの合成容量$C$は次のような関係式を満たす.
$\dfrac{1}{C}=\dfrac{1}{C_{1}}+\dfrac{1}{C_{2}}+\dots +\dfrac{1}{C_{n-1}}+\dfrac{1}{C_{n}}$
2.並列合成
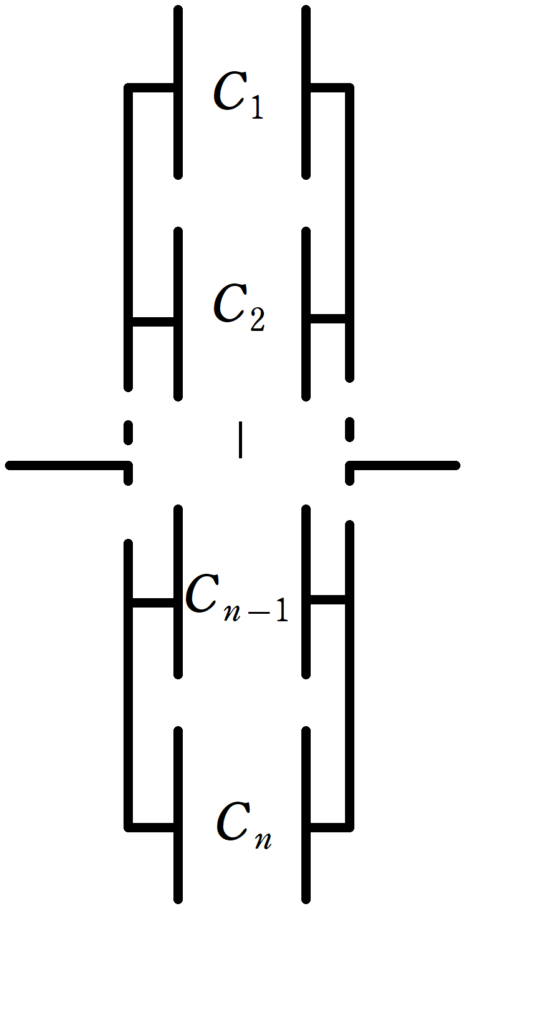
電気容量$C_{1}$,$C_{2}$,$\dots$,$C_{n-1}$,$C_{n}$の$n$個のコンデンサーを並列に結ぶ.
この$n$個のコンデンサーの合成容量$C$は次のような関係式を満たす.
$C=C_{1}+C_{2}+\dots +C_{n-1}+C_{n}$

直列合成は,条件があるんだね.
これらの式はどこから出てきたの?

コンデンサーの基本式と,電荷保存則,キルヒホッフ則を用いて示すことができます.
コンデンサーに蓄えられている電荷を$Q$,コンデンサー間の電圧を$V$とすれば,コンデンサーの電気容量$C$は
$C=\dfrac{Q}{V}$
実際は
$Q=CV$
として使うことが多い.
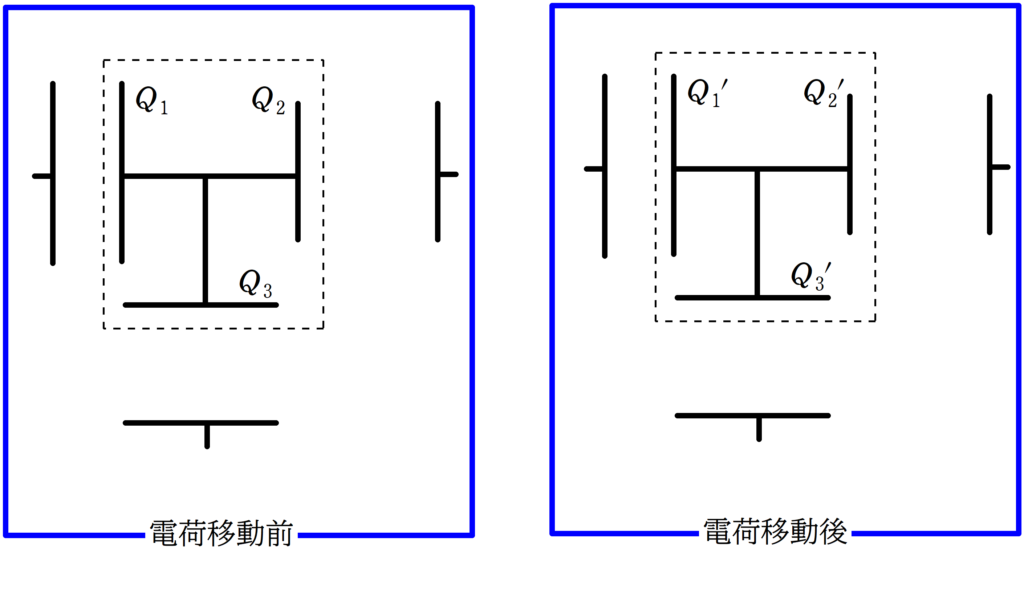
孤立した部分の電荷の総和は変化しない.これを電荷保存則という.
たとえば,上図のように点線部分の孤立した場所の電荷について考えると
$Q_{1}+Q_{2}+Q_{3}=Q_{1}^{\prime}+Q_{2}^{\prime}+Q_{3}^{\prime}$
が成り立つ.

では,直列の合成の式から導いていきましょう.
以下のように電荷を蓄えれている$n$個の直列コンデンサーを考えます.
ここで,条件として,各点線部分の電荷の和はそれぞれ0とします.
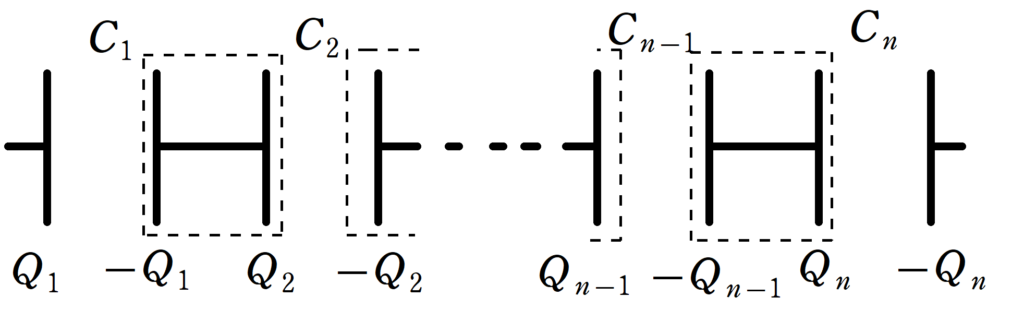
★ 電荷保存則
条件より,
$-Q_{1}+Q_{2}=0$,$-Q_{2}+Q_{3}=0$,$\dots$,$-Q_{n-1}+Q_{n}=0$
したがって,
$Q_{1}=Q_{2}=Q_{3}=\dots =Q_{n-1}=Q_{n}=Q$ $\dots (\ast)$
★ キルヒホッフ則
上図の$n$個のコンデンサーの電圧$V$は
$V=\dfrac{Q_{1}}{C_{1}}+\dfrac{Q_{2}}{C_{2}}+\dots +\dfrac{Q_{n-1}}{C_{n-1}}+\dfrac{Q_{n}}{C_{n}}$
$(\ast)$より
$\eqalign{V&=\dfrac{Q_{1}}{C_{1}}+\dfrac{Q_{2}}{C_{2}}+\dots +\dfrac{Q_{n-1}}{C_{n-1}}+\dfrac{Q_{n}}{C_{n}}\\&=\dfrac{Q}{C_{1}}+\dfrac{Q}{C_{2}}+\dots +\dfrac{Q}{C_{n-1}}+\dfrac{Q}{C_{n}}}$
したがって
$\dfrac{V}{Q}=\dfrac{1}{C_{1}}+\dfrac{1}{C_{2}}+\dots +\dfrac{1}{C_{n-1}}+\dfrac{1}{C_{n}}$ $\dots (2\ast)$
★ コンデンサーの基本式
ところで,コンデンサーの合成容量を$C$とすると
$Q=CV$ $\therefore \dfrac{1}{C}=\dfrac{V}{Q}$ $\dots (3\ast)$
$(2\ast)$,$(3\ast)$より
$\dfrac{1}{C}=\dfrac{1}{C_{1}}+\dfrac{1}{C_{2}}+\dots +\dfrac{1}{C_{n-1}}+\dfrac{1}{C_{n}}$

次に,並列の場合についてです.
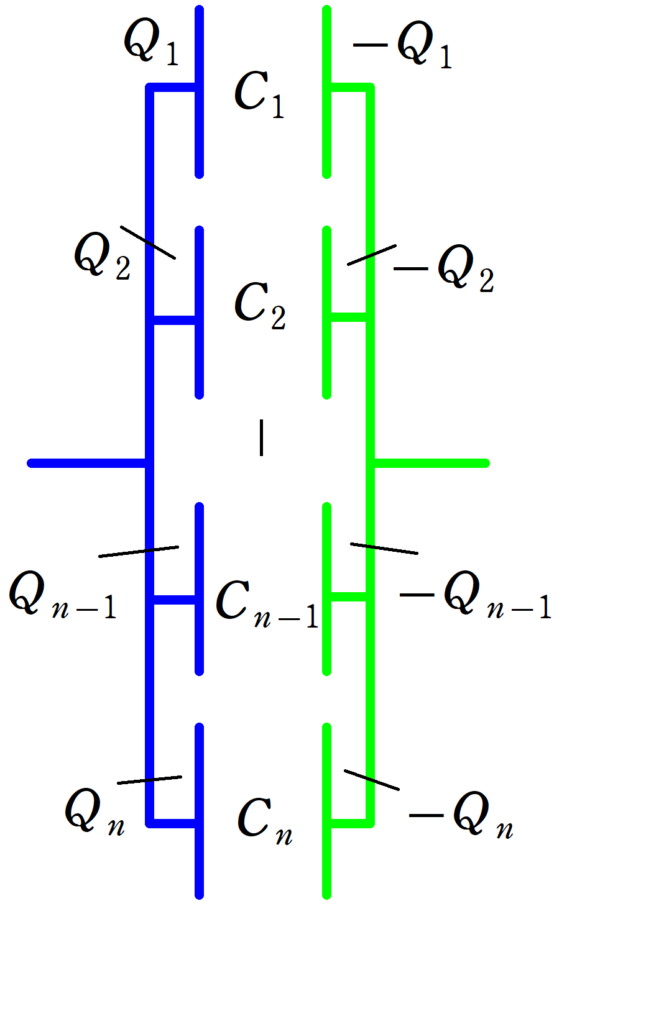

並列の場合は,すべてのコンデンサーにかかる電圧は同じとなりますね.
この電圧を$V$としましょう.
すると,各コンデンサーの基本式は次のようになります.
★ コンデンサーの基本式
$Q_{1}=C_{1}V$,$Q_{2}=C_{2}V$,$\dots$,$Q_{n-1}=C_{n-1}V$,$Q_{n}=C_{n}V$ $\dots (4\ast)$

$n$個のコンデンサーを1つのコンデンサーとみなします.
すると電荷の和$Q$は
$Q=Q_{1}+Q_{2}+\dots+Q_{n-1}+Q_{n}$
となります.
$(4\ast)$より
$\eqalign{Q&=Q_{1}+Q_{2}+\dots+Q_{n-1}+Q_{n}\\&=C_{1}V+C_{2}V+\dots+C_{n-1}V+C_{n}V\\&=(C_{1}+C_{2}\dots +C_{n-1}+C_{n})V}$
合成容量を$C$とすると,コンデンサーの基本式より,
$C=\dfrac{Q}{V}=C_{1}+C_{2}+\dots +C_{n-1}+C_{n}$

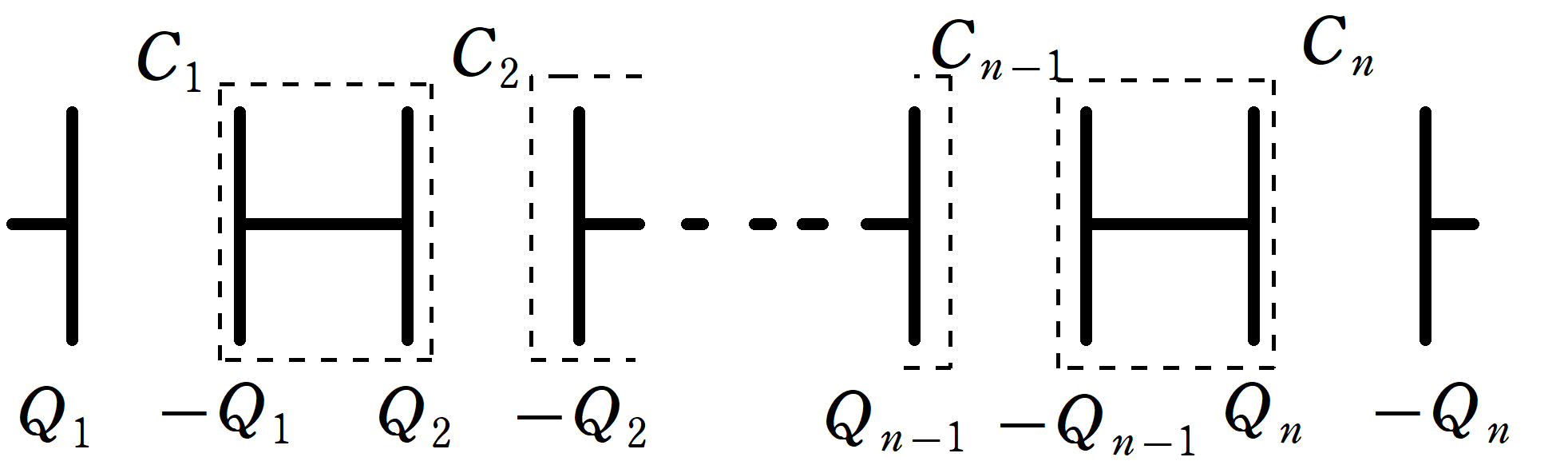
コメント
[…] コンデンサーの直列合成・並列合成 […]