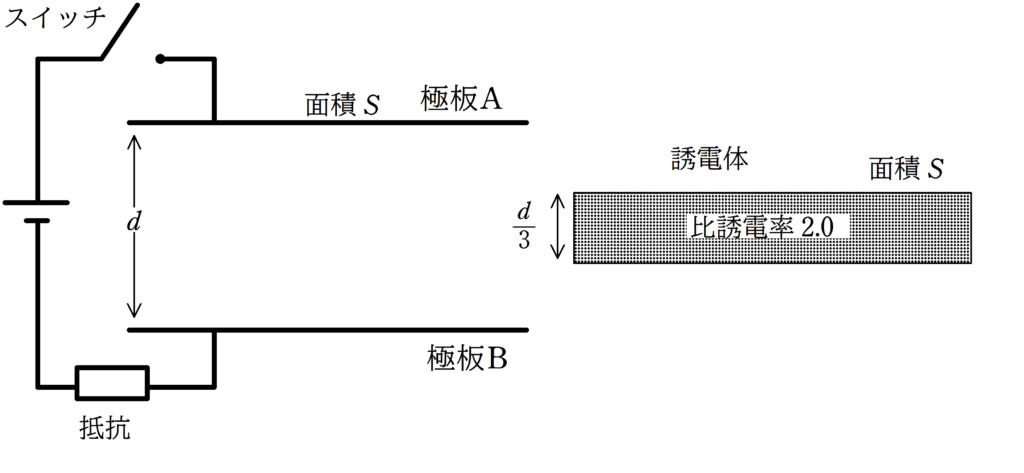
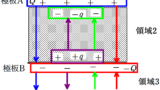
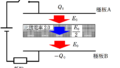
起電力$V_{0}$の電源,スイッチ,抵抗と面積$S$の極板A,Bによってつくられた平行平板コンデンサーが上図のように接続されている.
極板A,Bの距離は$d$に固定されており,真空の誘電率を$\varepsilon_{0}$とする.
なお,空気中での誘電率も真空と同じであるとみなすことができるとしてよい.
スイッチを閉じて十分時間が経った後,コンデンサー内部の電場は$E_{0}$となった.
その後スイッチを閉じたまま,ゆっくりと面積$S$,厚さ$\dfrac{d}{3}$で比誘電率$2.0$の誘電体を極板A,Bの中央に極板と平行に挿入した.
このとき,次の問いに答えよ.
ただし,解答には$\varepsilon_{0}$,$d$,$S$,$V_{0}$を用いよ.
(1) 誘電体を挿入した後に極板AとBにそれぞれ$Q_{1}$,$-Q_{1}$が蓄えられたとする.このとき,極板ABの電位差が$V_{0}$であることを用いて,$Q_{1}$を求めよ.
(2) 誘電体挿入後のコンデンサーの電気容量$C_{1}$を求めよ.
(3)
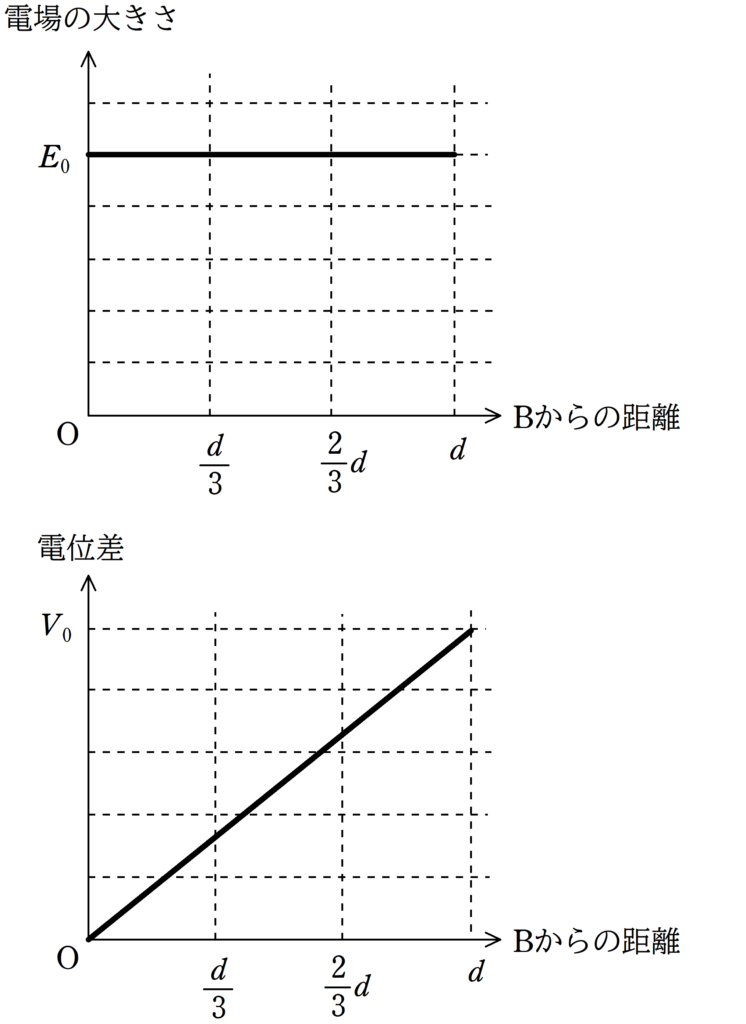
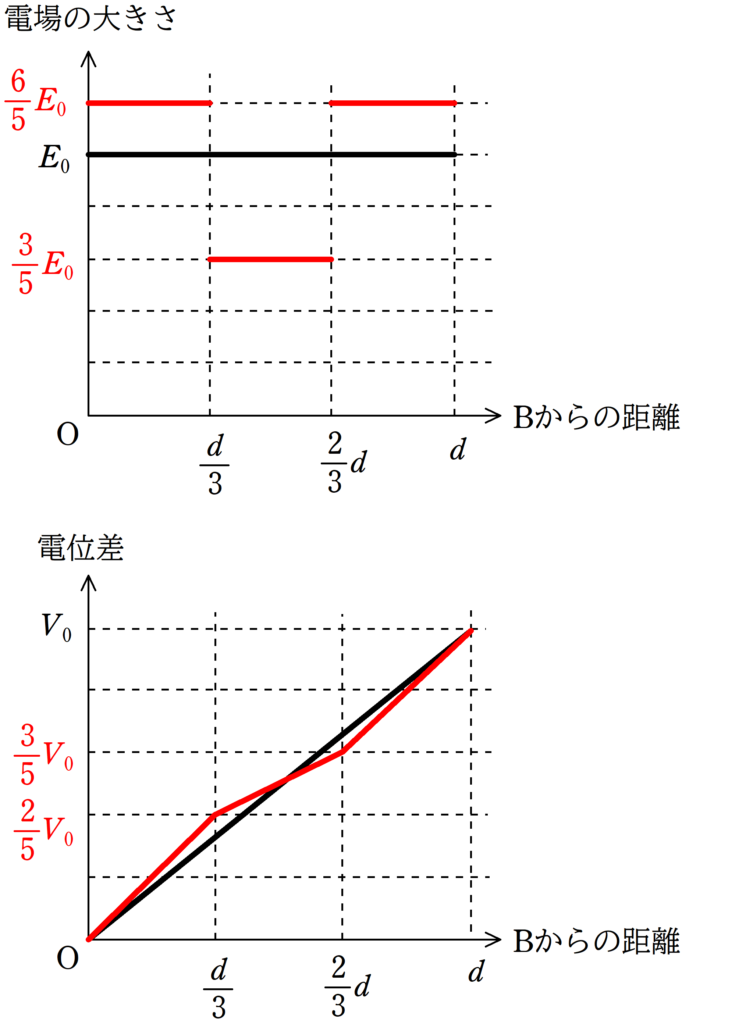
誘電体を挿入する前のBからの距離とコンデンサー内の電場の大きさの関係のグラフ,および,Bからの距離とBを基準とした電位の関係は上図のようであった.誘電体挿入後のグラフをかけ.
<解答>
(1)

極板A,Bに電荷$Q_{1}$,$-Q_{1}$が蓄えられたときに,これらの電荷によってつくられる電場の大きさ$E_{1}$は
$E_{1}=\dfrac{Q_{1}}{\varepsilon_{0}S}$
となるんだったね.
平面に分布した電荷がつくる電場と,各電荷がつくる電場の重ね合わせを考えれば理解できるよ.
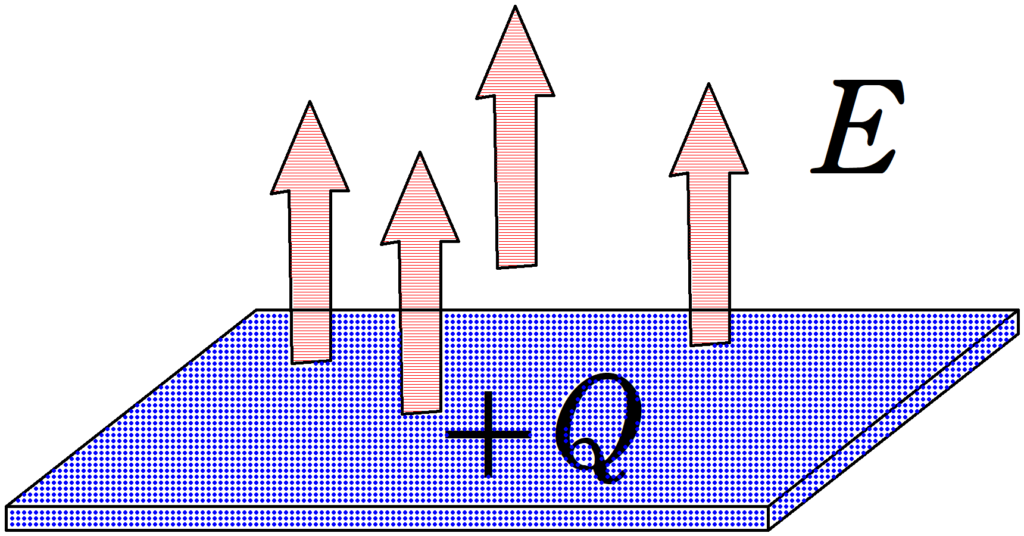
十分に広い平面に一様な電荷$Q$が分布している.
真空の誘電率を$\varepsilon_{0}$,平面の面積を$S$とするとき,電場の大きさ$E$は
$E=\dfrac{|Q|}{2\varepsilon_{0}S}$
これは,電場が距離によらず一定であることを意味している.
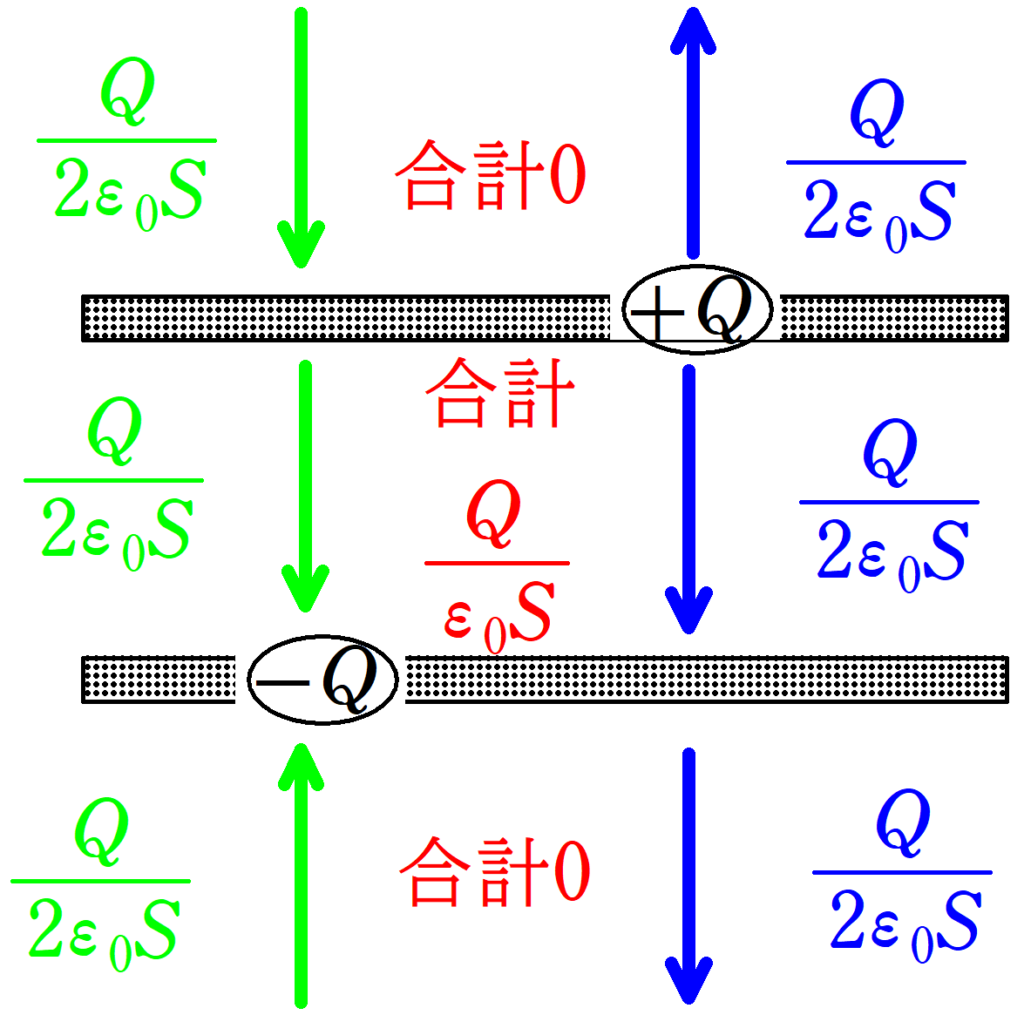

さらに,誘電体内部の電場は次のようになるよ.
この記事でも説明しているので,参考にしてね.
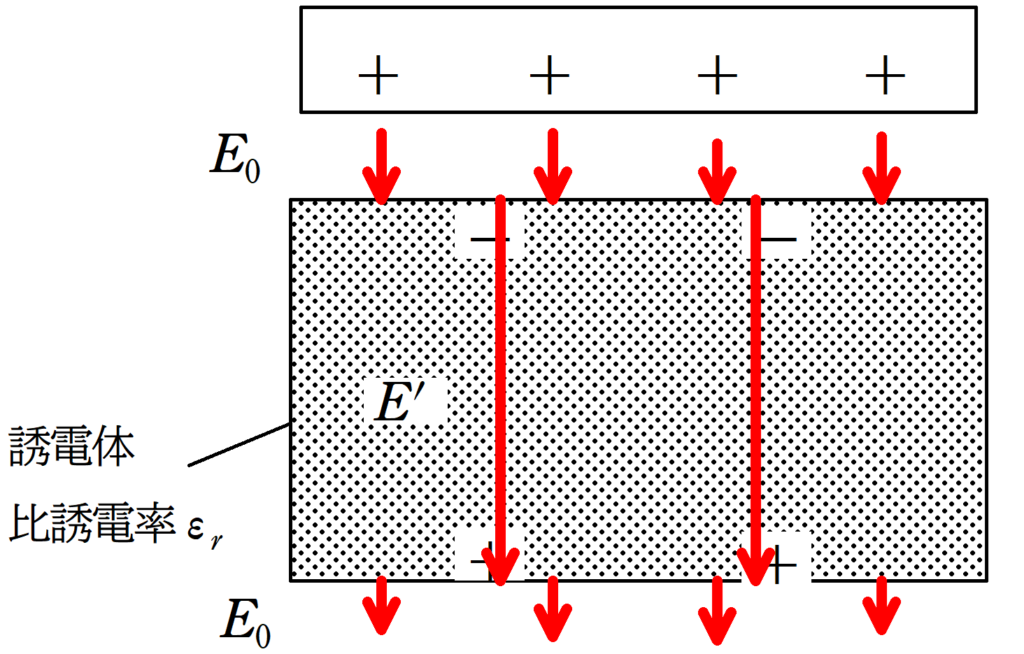
比誘電率$\varepsilon_{\rm r}$の誘電体に外部電場$E_{0}$をかけると,誘電分極により,誘電体内部の電場が$E^{\prime}$になったとする.
このとき,
$E^{\prime}=\dfrac{E_{0}}{\varepsilon_{\rm r}}$
となるように,比誘電率を定義する.

つまり,誘電体内部の電場の大きさは比誘電率が$2.0$であることから,$\dfrac{E_{1}}{2}$となるよ.
電池をつないだまま誘電体を挿入するので,極板ABの電位差と電源の電位差は等しいね.
次の関係を使って,式を立ててみましょう.
電場の大きさを$E$,距離$\Delta x$の電位差を$\Delta V$とするとき,次の関係が成り立つ.
$E=\left|\dfrac{\Delta V}{\Delta x}\right|$
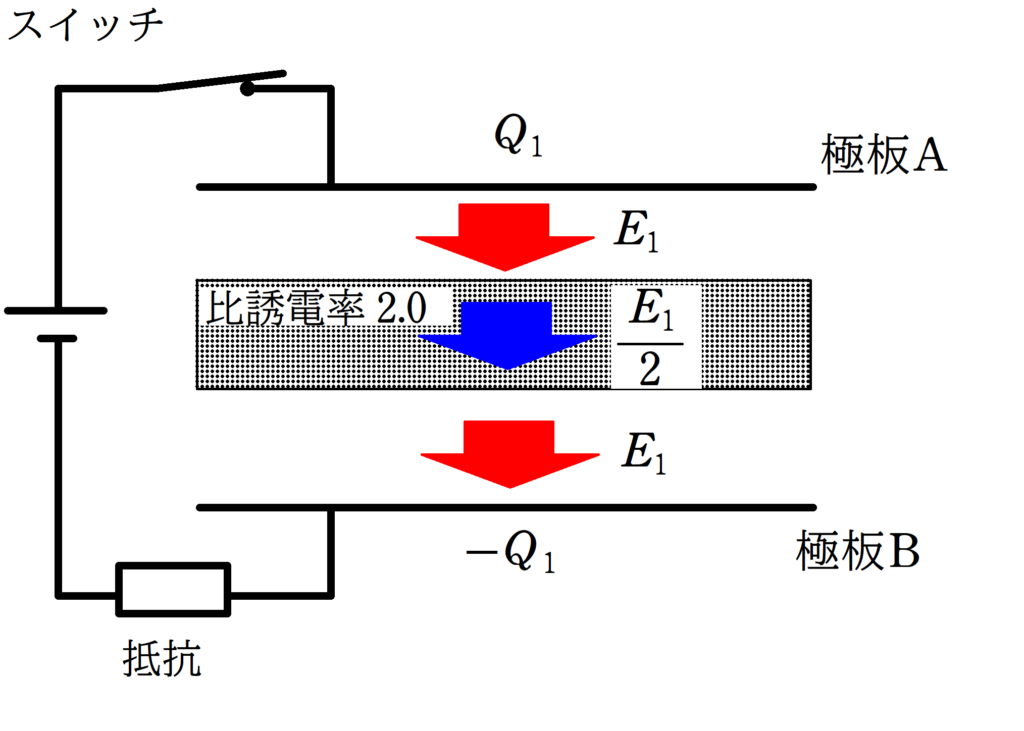
★ 極板ABの電位差の式
$\eqalign{V_{0}&=E_{1}\cdot \dfrac{d}{3}+\dfrac{E_{1}}{2}\dfrac{d}{3}+E_{1}\cdot \dfrac{d}{3}\\&=\dfrac{5}{6}E_{1}d}$
$E_{1}=\dfrac{Q_{1}}{\varepsilon_{0}S}$を代入して
$V_{0}=\dfrac{5}{6}\cdot \dfrac{Q_{1}}{\varepsilon_{0}S}\cdot d$
$Q_{1}$について解いて
$Q_{1}=\dfrac{6\varepsilon_{0}S}{5d}V_{0}$
(2)

(1)で得た式を利用して,コンデンサーの電気容量を求めてみましょう.
コンデンサーに蓄えられている電荷を$Q$,コンデンサー間の電圧を$V$とすれば,コンデンサーの電気容量$C$は
$C=\dfrac{Q}{V}$
実際は
$Q=CV$
として使うことが多い.
★ 誘電体挿入後のコンデンサーの電気容量$C_{1}$
$C_{1}=\dfrac{Q_{1}}{V_{0}}=\dfrac{6\varepsilon_{0}S}{5d}$
したがって,答えは,$C_{1}=\dfrac{6\varepsilon_{0}S}{5d}$
(3)

誘電体挿入前のコンデンサー内の電場$E_{0}$は
$E_{0}=\dfrac{V_{0}}{d}$
だね.
一方,誘電体挿入後は(1)で考えたように
$E_{1}=\dfrac{Q_{1}}{\varepsilon_{0}S}$
であって,ここに,$Q_{1}=\dfrac{6\varepsilon_{0}S}{5d}V_{0}$を代入すると
$E_{1}=\dfrac{1}{\varepsilon_{0}S}\cdot \dfrac{6\varepsilon_{0}S}{5d}V_{0}=\dfrac{6V_{0}}{5d}=\dfrac{6}{5}E_{0}$
となるんだね.
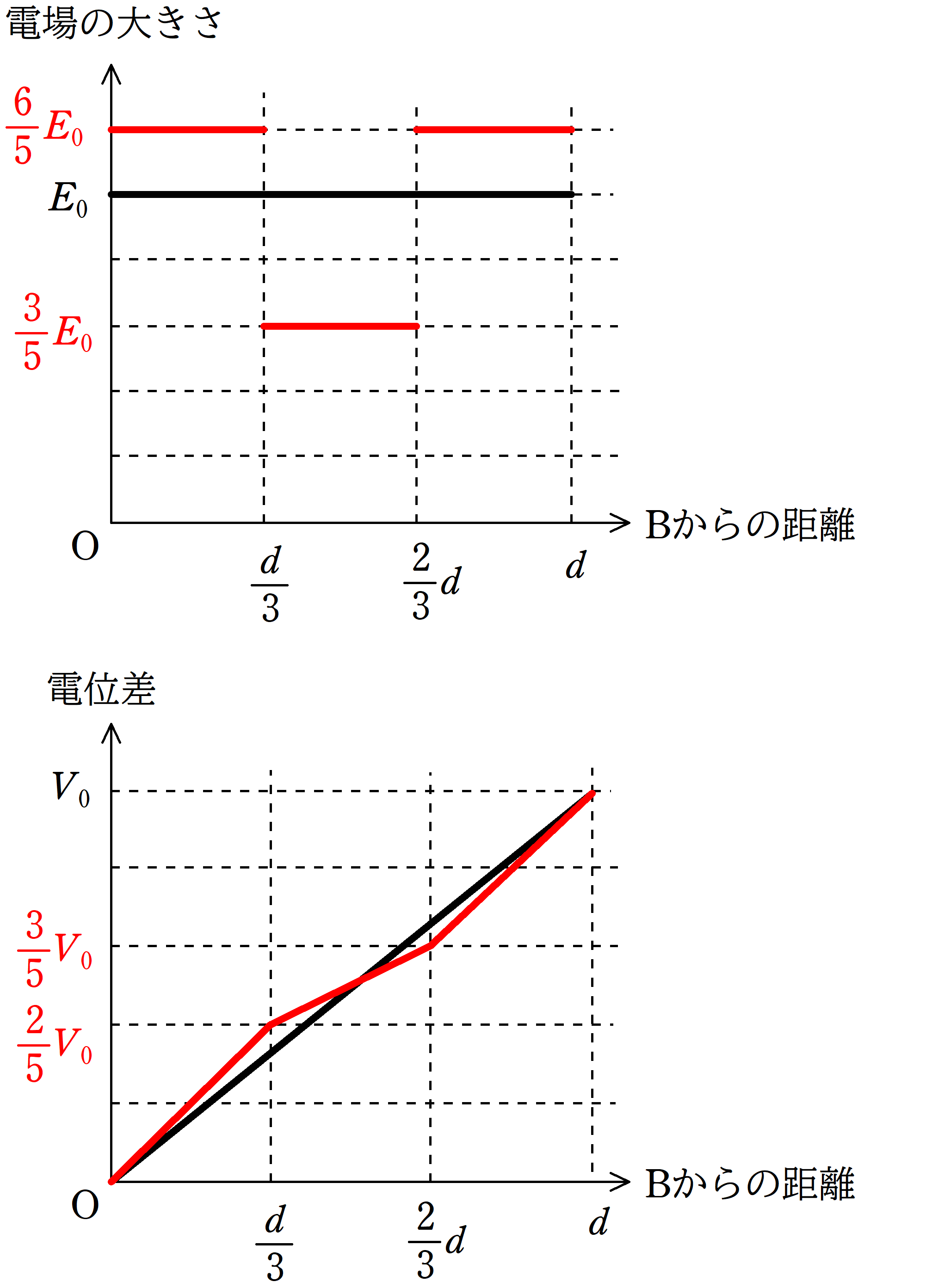
だから,グラフは次のようになるよ.

コメント