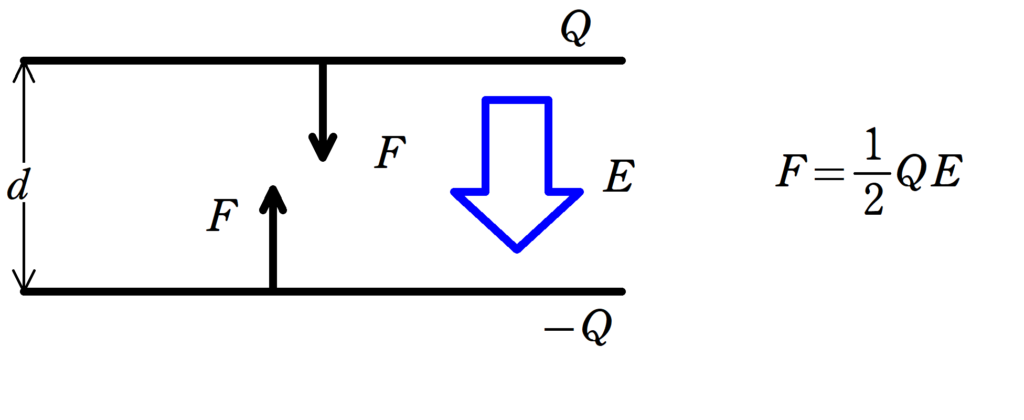

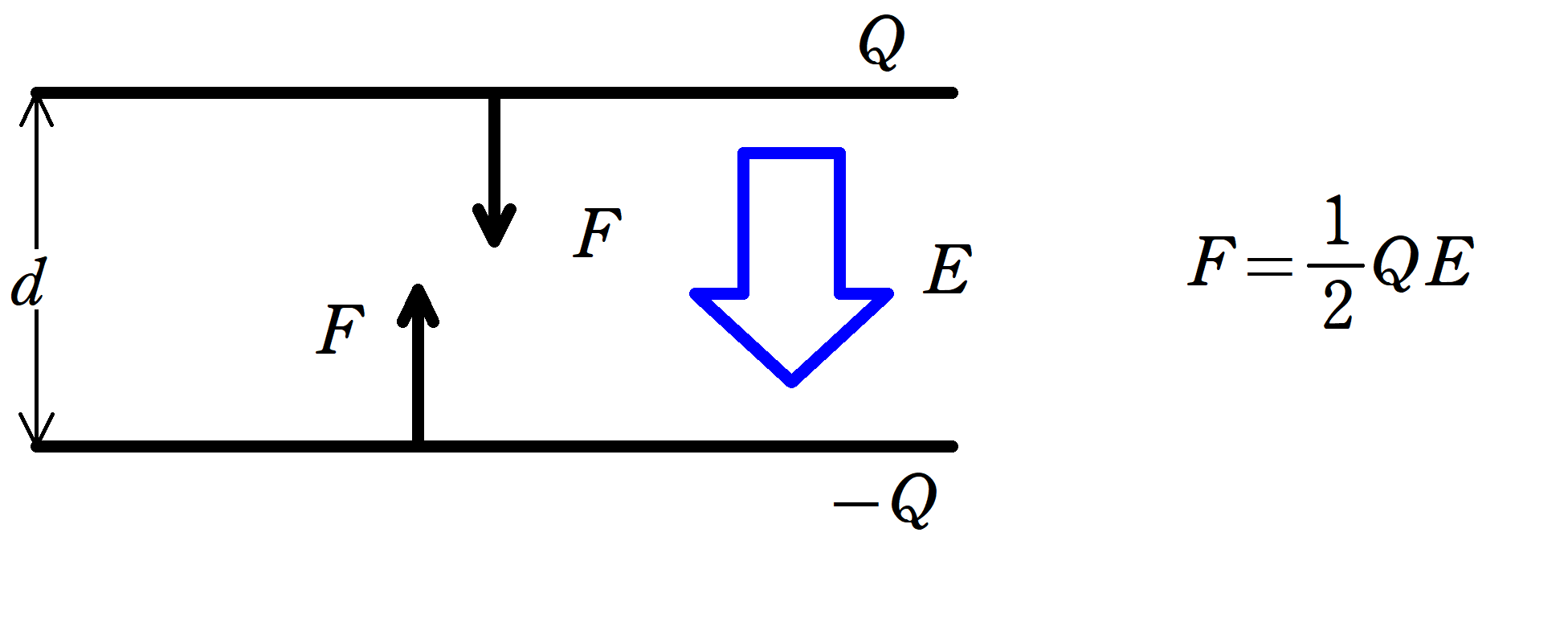
上図のように,面積$S$の平行平板コンデンサーがあって,極板に蓄えられている電荷が$Q$,$-Q$とします.
コンデンサー間の電場の大きさを$E$とすると,極板にはたらく引力$F$は
$F=\dfrac{1}{2}QE$
だったんだよ.
なんで,
$F=QE$
じゃないんだろう??

そうですね.
まずは,次の2つを理解しておきましょう.
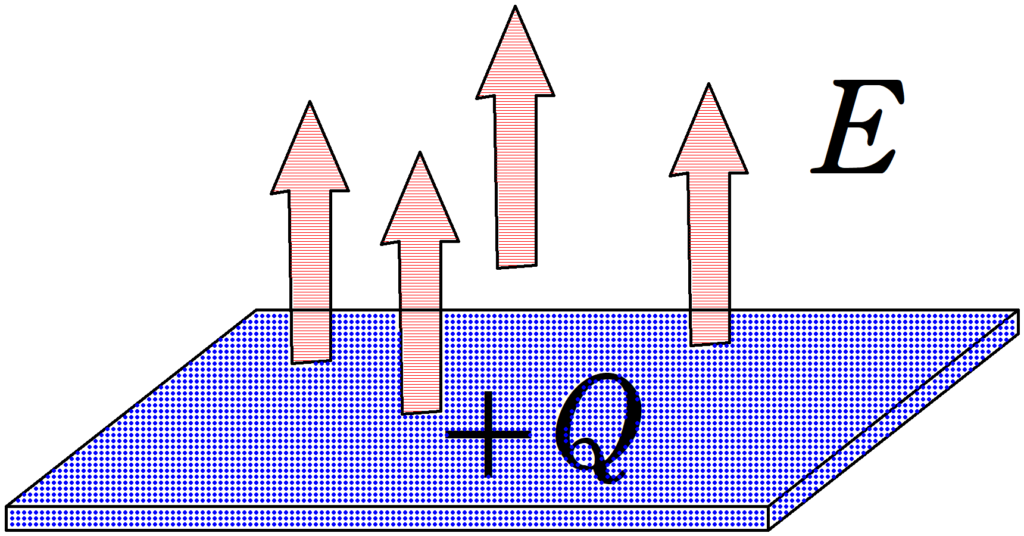
十分に広い平面に一様な電荷$Q$が分布している.
真空の誘電率を$\varepsilon_{0}$,平面の面積を$S$とするとき,電場の大きさ$E$は
$E=\dfrac{|Q|}{2\varepsilon_{0}S}$
これは,電場が距離によらず一定であることを意味している.
電場の大きさ$E$の場所に電荷$q$をおいたときにはたらく静電気力の大きさ$F$は
$F=|q|E$
※ ただし,この電場$E$は,電荷$q$がつくる電場は含まない.

それぞれの電荷は次のような電場をつくるんだね.
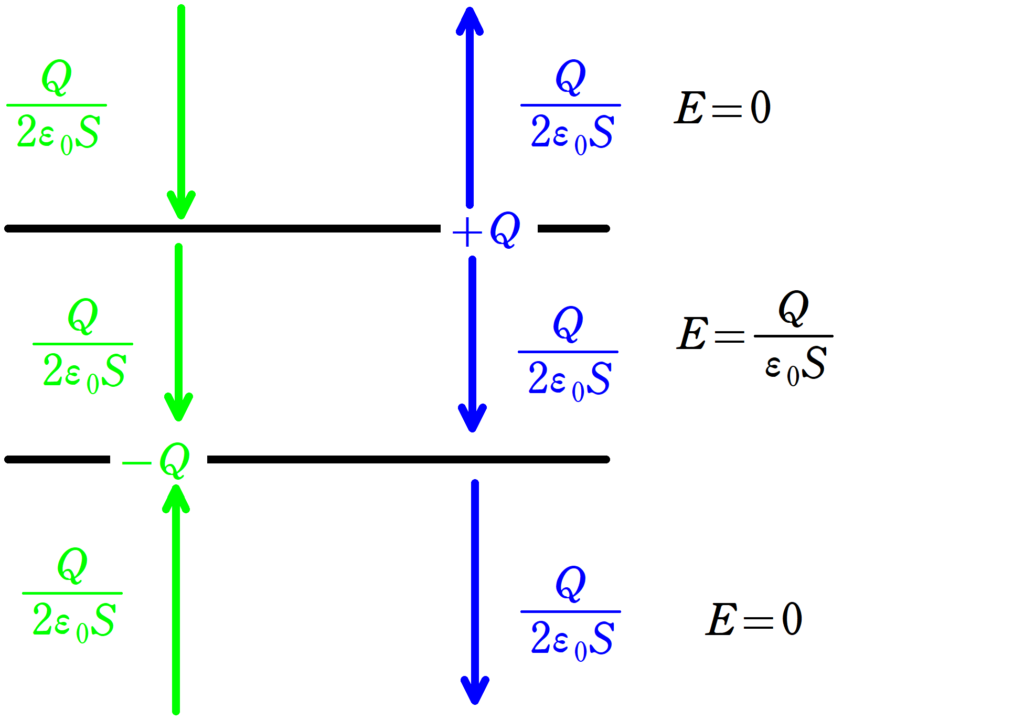

電場$E=\dfrac{Q}{\varepsilon_{0}S}$は$Q$と$-Q$それぞれがつくった電場を重ね合わせたものだね.
電荷$Q$が受ける力$F$は,電荷$-Q$がつくる電場$\dfrac{E}{2}=\dfrac{Q}{2\varepsilon_{0}S}$を用いて
$F=$$Q$$\cdot$ $\dfrac{E}{2}$
となるんだね.
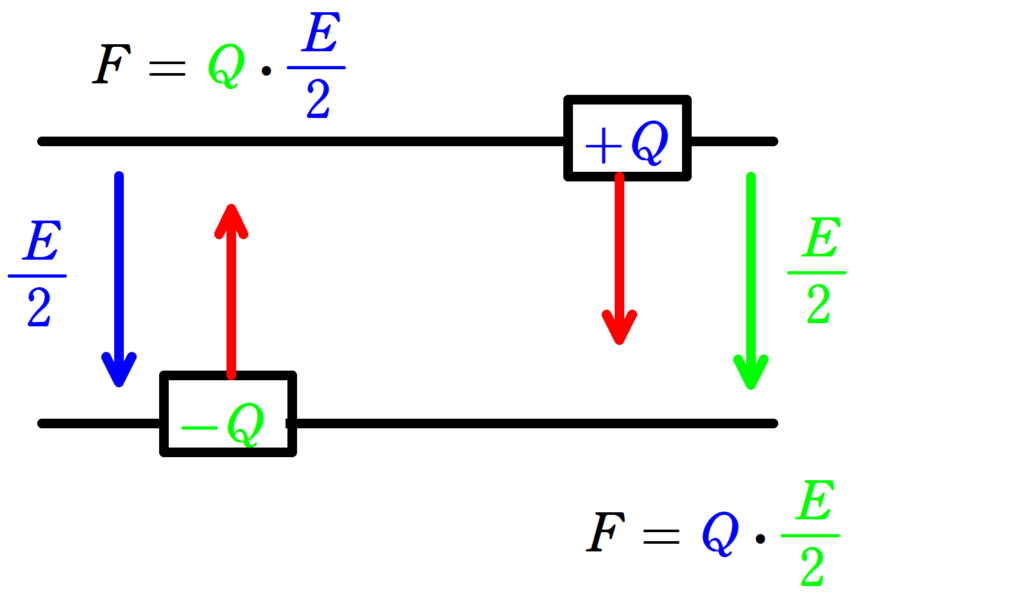

そういうことです.
$F=\dfrac{1}{2}QE$
というよりは,
$F=Q\cdot \dfrac{E}{2}$
と理解しておくとよいでしょう.

また,極板間にはたらく力は,静電エネルギーの変化を計算することでも確かめることができます.
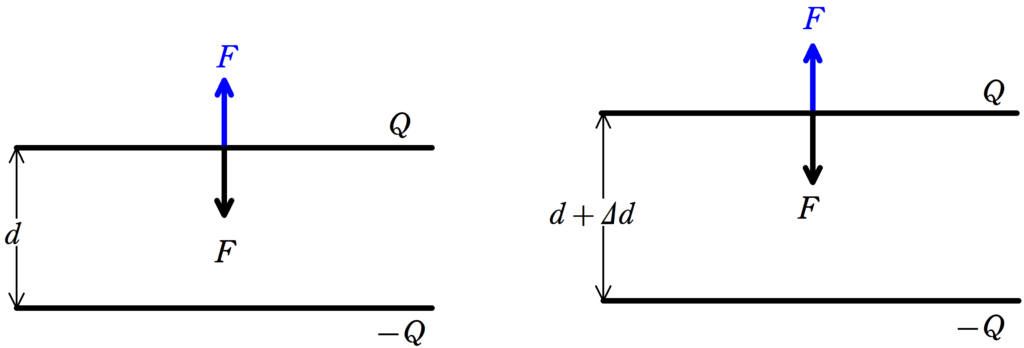

$-Q$を蓄えている方の極板を固定して,$Q$の方の極板に力を加えてゆっくと距離を$d$から$d+\Delta d$に広げます.
このときに加える力の大きさを$F$として,$\Delta d$が非常に小さいため,力$F$は変化しないとします.
このとき,力$F$した仕事$W$は
$W=F\Delta d$ $\dots (\ast)$
となります.
また,静電エネルギーの変化を$\Delta U$を計算します.
電気容量$C$のコンデンサーに電荷$Q$が蓄えられていて,電圧が$V$のときの,静電エネルギー$U$は
$U=\dfrac{1}{2}QV=\dfrac{1}{2}CV^{2}=\dfrac{Q^{2}}{2C}$
★ はじめの静電エネルギー$U_{1}$
$\eqalign{U_{1}&=\dfrac{Q^{2}}{2\varepsilon_{0}\dfrac{S}{d}}\\&=\dfrac{Q^{2}d}{2\varepsilon_{0}S}}$
★ 移動後の静電エネルギー$U_{2}$
$\eqalign{U_{2}&=\dfrac{Q^{2}}{2\varepsilon_{0}\dfrac{S}{d+\Delta d}}\\&=\dfrac{Q^{2}(d+\Delta d)}{2\varepsilon_{0}S}}$
★ 静電エネルギーの変化$\Delta U$
$\eqalign{\Delta U&=U_{2}-U_{1}\\&=\dfrac{Q^{2}(d+\Delta d)}{2\varepsilon_{0}S}-\dfrac{Q^{2}d}{2\varepsilon_{0}S}\\&=\dfrac{Q^{2}\Delta d}{2\varepsilon_{0}S} \dots (2\ast)}$

静電エネルギーの変化$\Delta U$は仕事$W$は等しいので,次の関係式が成り立つね.
$W=F\Delta d$ $\dots (\ast)$と$\Delta U=\dfrac{Q^{2}\Delta d}{2\varepsilon_{0}S}$ $\dots (2\ast)$より
$\eqalign{W&=\Delta U\cr F\Delta d&=\dfrac{Q^{2}\Delta d}{2\varepsilon_{0}S}\cr F\Delta d&=\dfrac{Q^{2}\Delta d}{2\varepsilon_{0}S}}$
したがって
$\eqalign{F&=\dfrac{Q^{2}}{2\varepsilon_{0}S}\\&=Q\cdot \dfrac{Q}{2\varepsilon_{0}S}\\&=Q\cdot \dfrac{E}{2}}$

$E=\dfrac{Q}{\varepsilon_{0}S}$としました.
たしかに,$F=Q\cdot \dfrac{E}{2}$になったね.

コメント
[…] コンデンサーの極板間にはたらく力は$F=QE$ではない […]