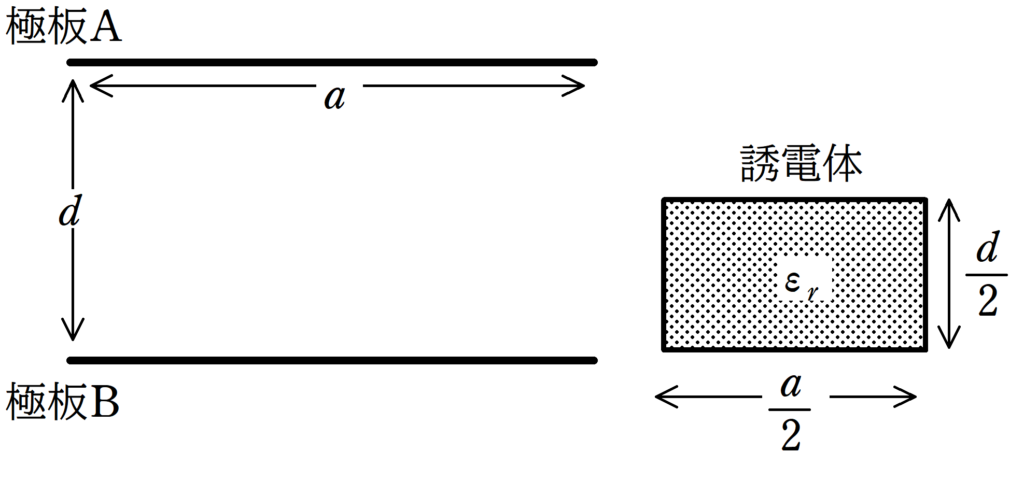
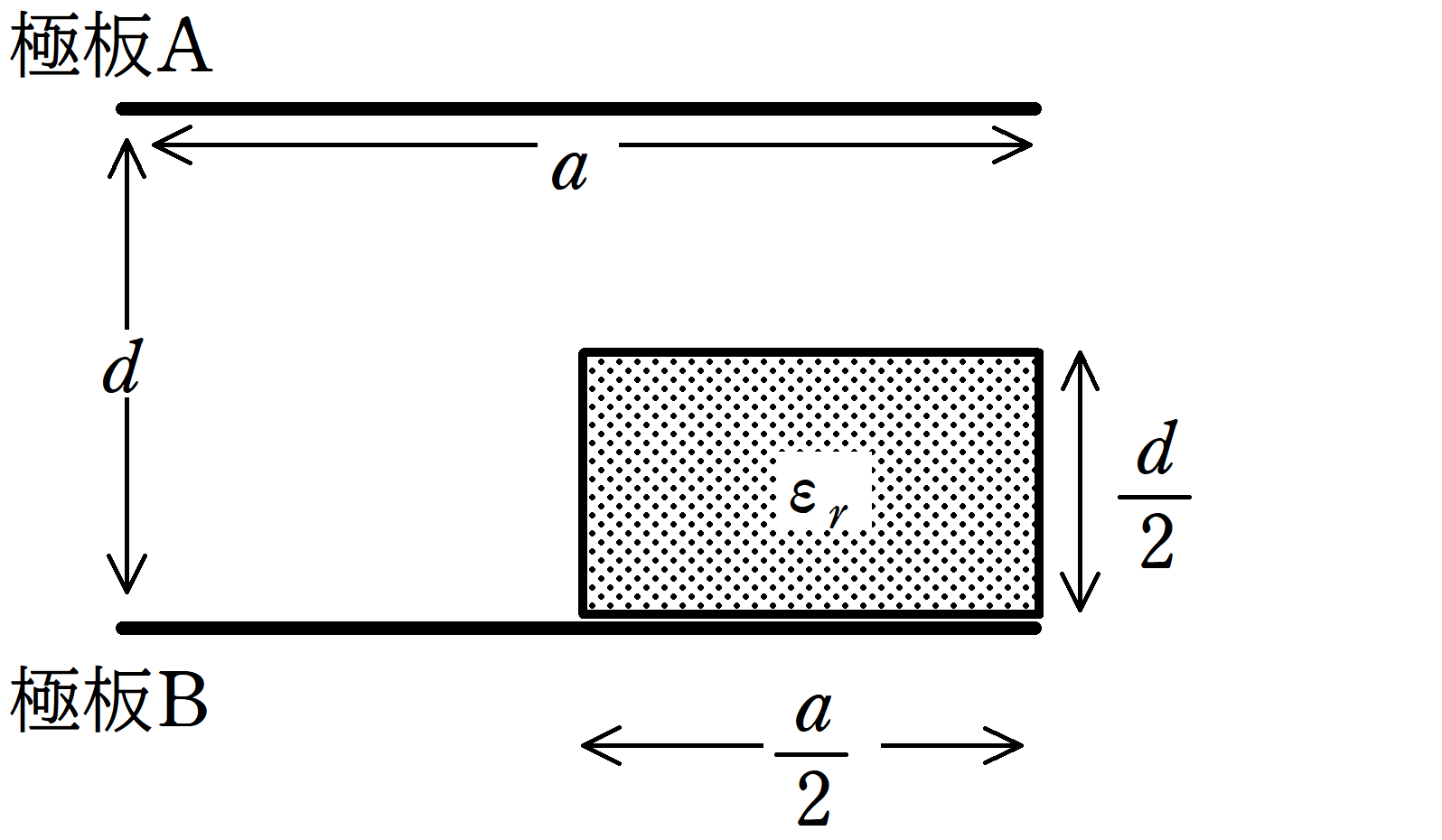
上図のように,一辺の長さ$a$の正方形極板A,Bを距離$d$だけ隔てて固定し,コンデンサーをつくる.
このコンデンサーに一辺の長さが$\dfrac{a}{2}$,高さ$\dfrac{d}{2}$で,比誘電率$\varepsilon_{r}$の誘電体を次図のような位置に挿入する.
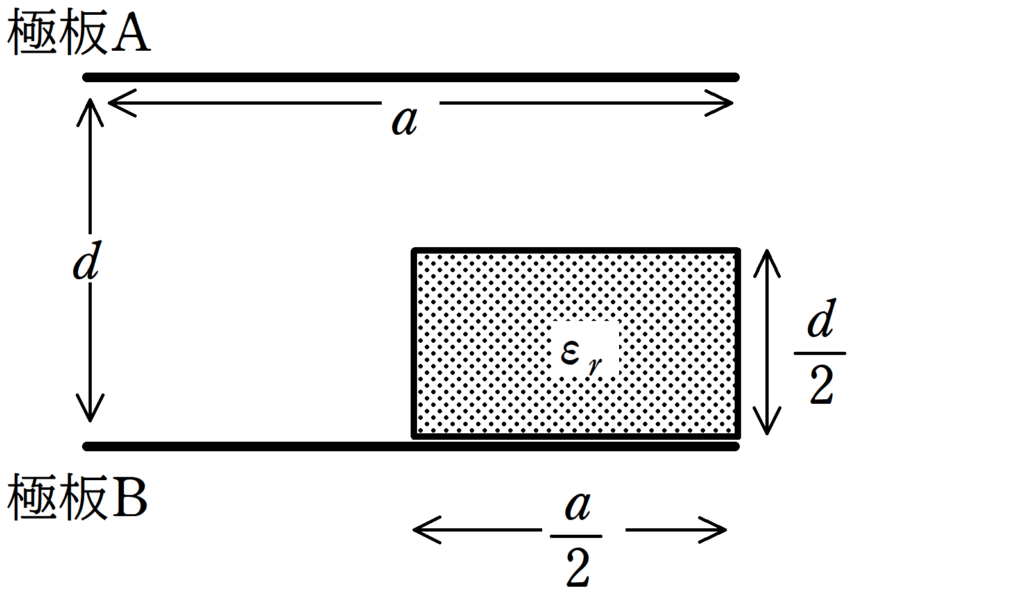
このとき,誘電体を挿入したときのコンデンサーの合成容量を求めよ.
ただし,このコンデンサーは真空中にあるとし,真空の誘電率を$\varepsilon_{0}$とする.
<解答>

平行板コンデンサーの電気容量の式と,合成の式を使って,効率的に計算してみましょう.
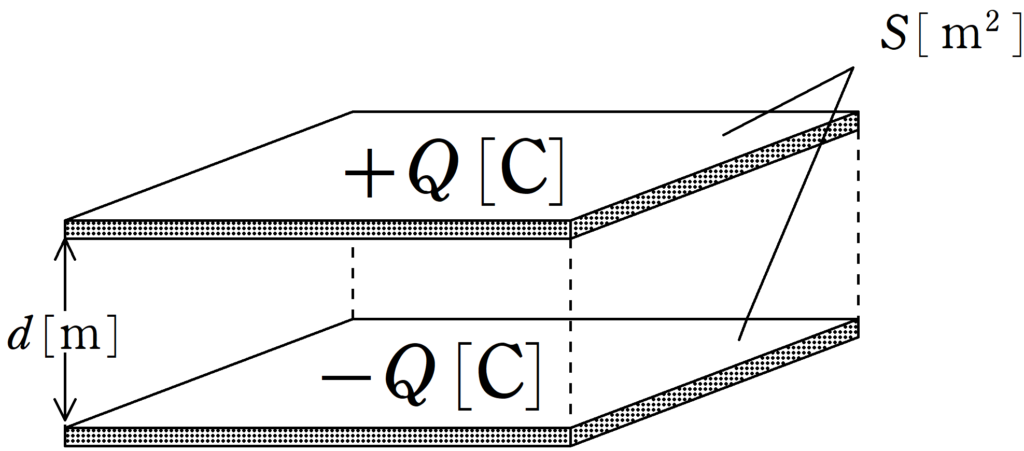
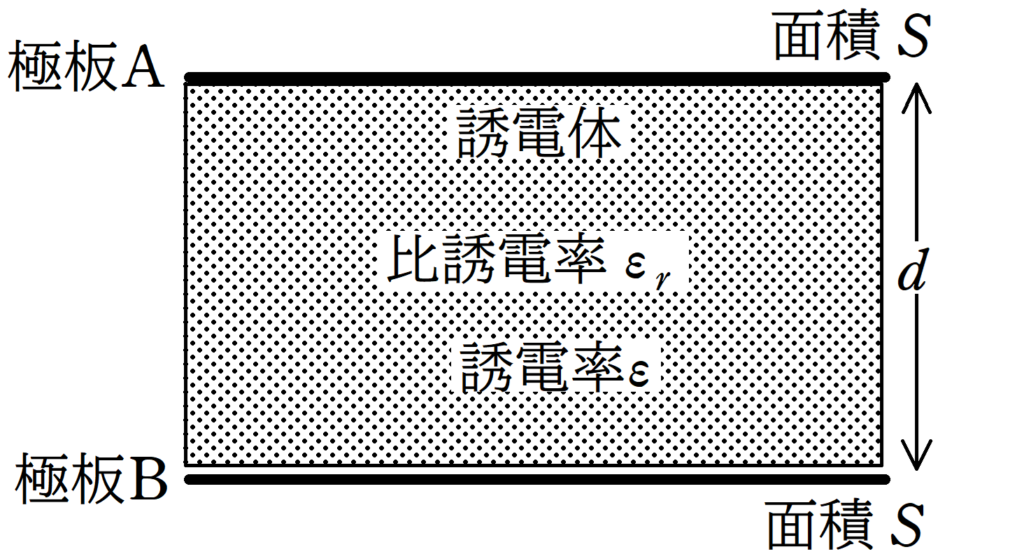
面積$S[\rm m^2]$の平らな導体板2枚を距離$d[\rm m]$だけ隔てて固定する.
真空の誘電率を$\varepsilon_{0}[\rm F/m]$とする.真空中において,このコンデンサーの電気容量$C_{0}[\rm F]$は次のようになる.
$C_{0}=\varepsilon_{0}\dfrac{S}{d}$
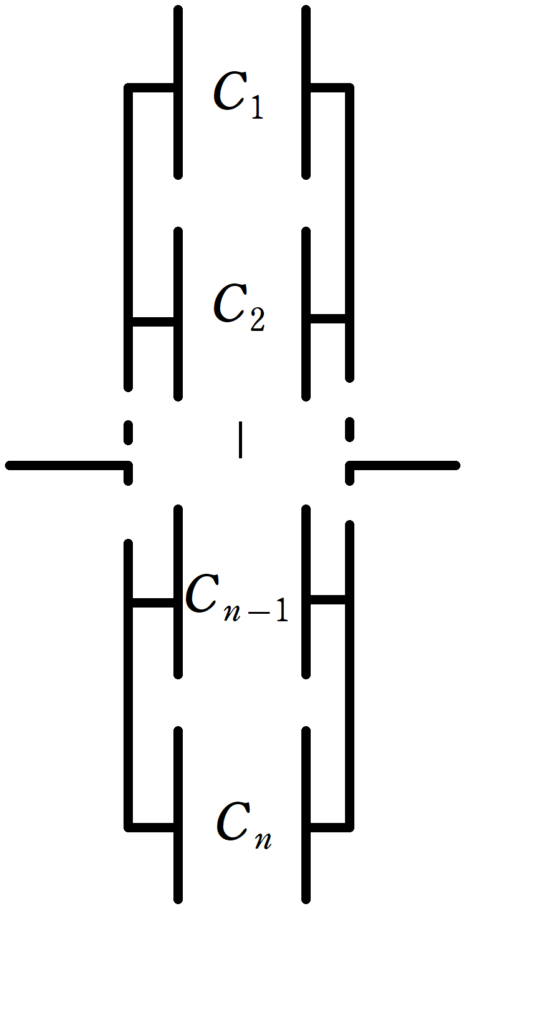
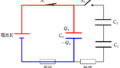
1.直列合成
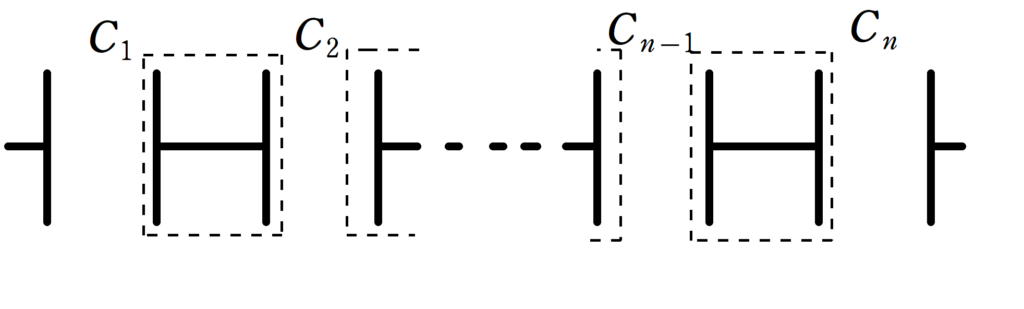
電気容量$C_{1}$,$C_{2}$,$\dots$,$C_{n-1}$,$C_{n}$の$n$個のコンデンサーを直列に結ぶ.
上図のように,点線で囲まれた各部分の電荷の和が0のとき,この$n$個のコンデンサーの合成容量$C$は次のような関係式を満たす.
$\dfrac{1}{C}=\dfrac{1}{C_{1}}+\dfrac{1}{C_{2}}+\dots +\dfrac{1}{C_{n-1}}+\dfrac{1}{C_{n}}$
2.並列合成
電気容量$C_{1}$,$C_{2}$,$\dots$,$C_{n-1}$,$C_{n}$の$n$個のコンデンサーを直列に結ぶ.
この$n$個のコンデンサーの合成容量$C$は次のような関係式を満たす.
$C=C_{1}+C_{2}+\dots +C_{n-1}+C_{n}$

真空部分と誘電体部分に分けてみると,次のようになるね.
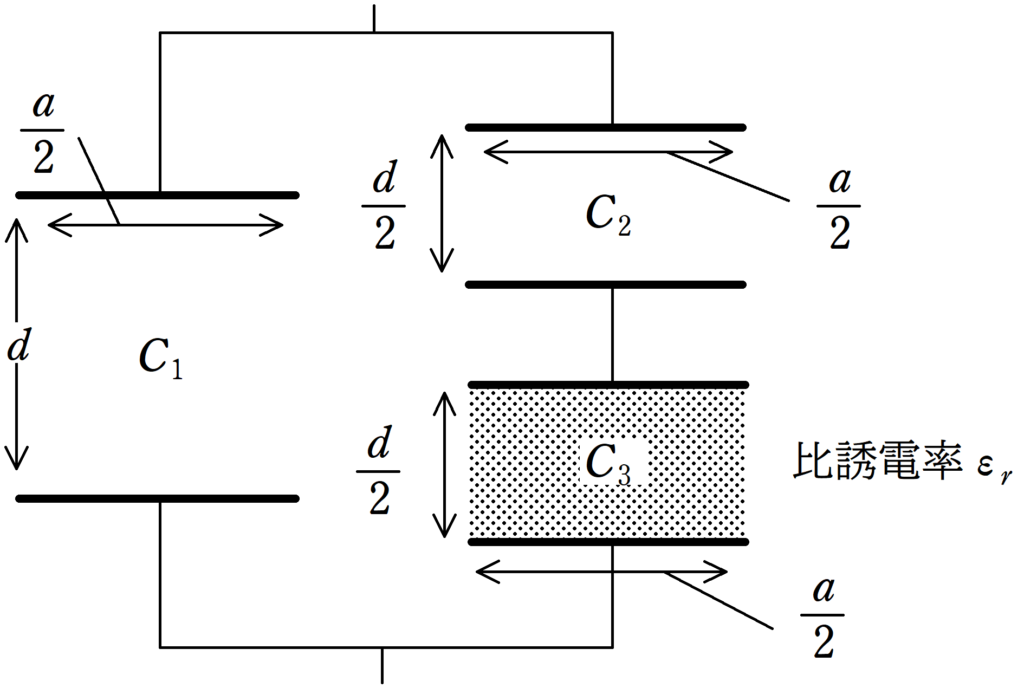

左側部分の電気容量を$C_{1}$,右側の真空部分の電気容量を$C_{2}$,右側の誘電体部分の電気容量を$C_{3}$としましょう.
まずは,$C_{2}$と$C_{3}$を直列合成し,その電気容量$C_{23}$を求め,次に,$C_{1}$と$C_{23}$を並列合成し,その電気容量$C_{123}$を求めます.
★ $C_{1}$の電気容量
$\eqalign{C_{1}&=\varepsilon_{0}\dfrac{\dfrac{a}{2}\cdot a}{d}\\&=\varepsilon_{0}\dfrac{a^{2}}{2d}}$
★ $C_{2}$の電気容量
$\eqalign{C_{2}&=\varepsilon_{0}\dfrac{\dfrac{a}{2}\cdot a}{\dfrac{d}{2}}\\&=\varepsilon_{0}\dfrac{a^{2}}{d}}$

誘電体が挿入された場合の電気容量は次のようになるんだったね.
極板面積$S$の平板A,Bを距離$d$だけ隔てて固定しておく.
真空の誘電率を$\varepsilon_{0}$とすると,極板A,Bに何も入っていない場合の電気容量$C_{0}$は次のようになる.
$C_{0}=\varepsilon_{0}\dfrac{S}{d}$
このコンデンサーに比誘電率$\varepsilon_{\rm r}$,誘電率$\varepsilon$の誘電体で満たすとき,電気容量$C$は次のようになる.
$\eqalign{C&=\varepsilon\dfrac{S}{d}\\&=\varepsilon_{\rm r}\varepsilon_{0}\dfrac{S}{d}\\&=\varepsilon_{\rm r}C_{0}}$
また,$\varepsilon_{0}$,$\varepsilon$,$\varepsilon_{\rm r}$は次の関係がある.
$\varepsilon_{\rm r}=\dfrac{\varepsilon}{\varepsilon_{0}}$
★ $C_{3}$の電気容量
コンデンサーの形状,面積,極板間の距離は$C_{2}$と同じなので,
$\eqalign{C_{3}&=\varepsilon_{r}C_{2}\\&=\varepsilon_{r}\varepsilon_{0}\dfrac{a^{2}}{d}}$
★ $C_{2}$と$C_{3}$の合成
直列合成をする.
$\eqalign{\dfrac{1}{C_{23}}&=\dfrac{1}{C_{2}}+\dfrac{1}{C_{3}}\\&=\dfrac{d}{\varepsilon_{0}a^{2}}+\dfrac{d}{\varepsilon_{r}\varepsilon_{0}a^{2}}\\&=\dfrac{d}{\varepsilon_{0}a^{2}}(1+\dfrac{1}{\varepsilon_{r}})\\&=\dfrac{(\varepsilon_{r}+1)d}{\varepsilon_{r}\varepsilon_{0}a^{2}}}$
$\therefore$ $C_{23}=\dfrac{\varepsilon_{r}\varepsilon_{0}a^{2}}{(\varepsilon_{r}+1)d}$
★ $C_{1}$と$C23$の合成
並列合成する.
$\eqalign{C_{123}&=C_{1}+C_{23}\\&=\varepsilon_{0}\dfrac{a^{2}}{2d}+\dfrac{\varepsilon_{r}\varepsilon_{0}a^{2}}{(\varepsilon_{r}+1)d}\\&=\varepsilon_{0}\dfrac{a^{2}}{d}(\dfrac{1}{2}+\dfrac{\varepsilon_{r}}{\varepsilon_{r}+1})\\&=\dfrac{\varepsilon_{0}(3\varepsilon_{r}+1)a^{2}}{2(\varepsilon_{r}+1)d}}$

合成の式を使えば,簡単に合成容量を計算できるね.

コメント