
今回は,「静止流体の圧力」の求め方についての話です.
ここは割と苦手とする人が多いようなので,演習問題まで解いてチェックするとよいでしょう.
まず,パスカルの原理です.
密閉された液体の一部に加えられた圧力はその強さを変えることなく,液体の各部分に伝えられる.
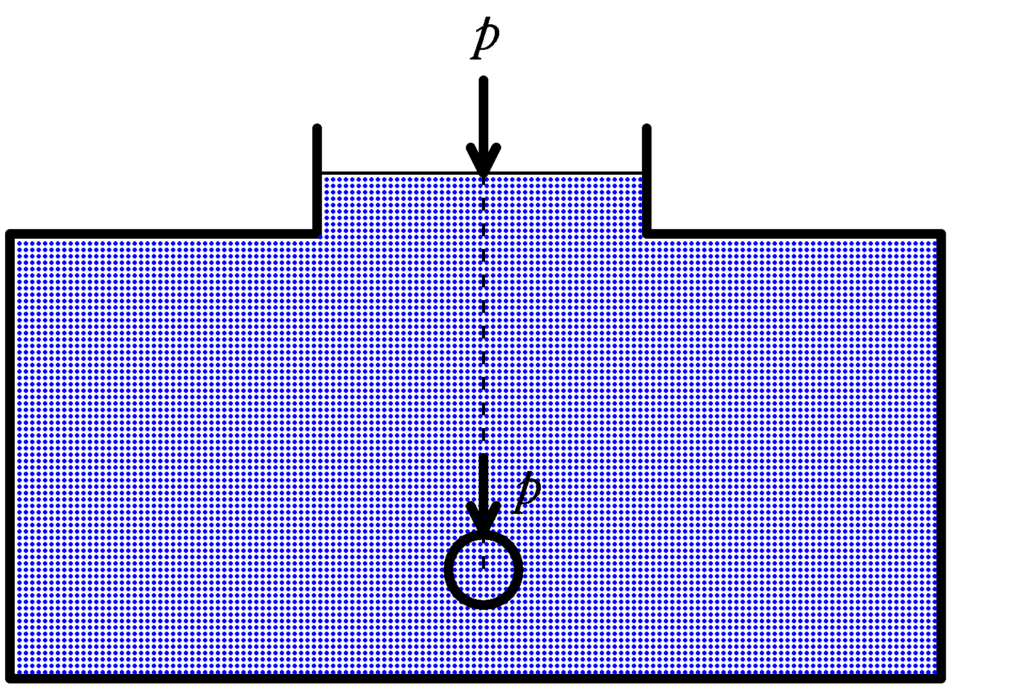

静止流体を考えているので,液体はすべてつりあっています.
次のように,2つの物体の及ぼす力(下図は断面が単位面積)と同じです.
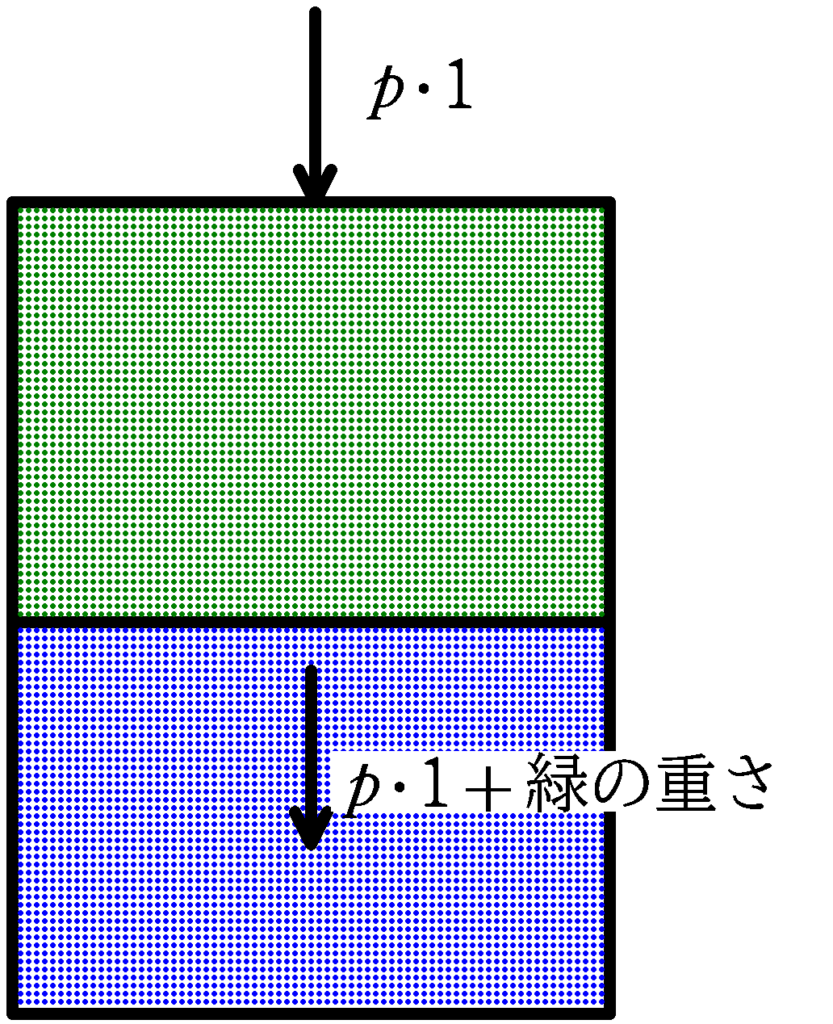

次の記事でも説明しているね.

では,次の問題を考えてみましょう.
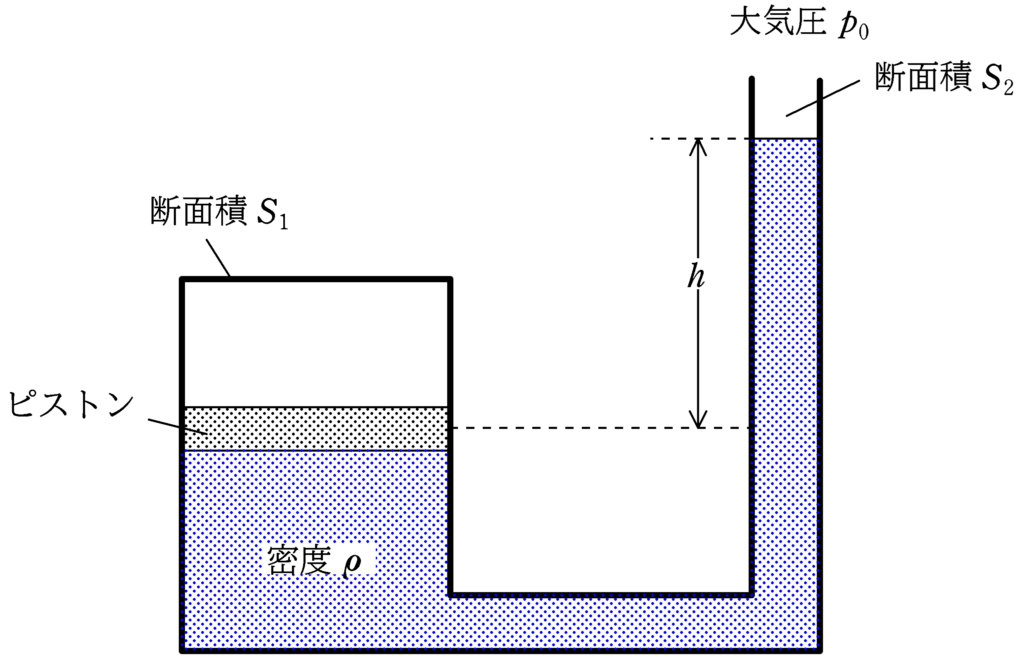
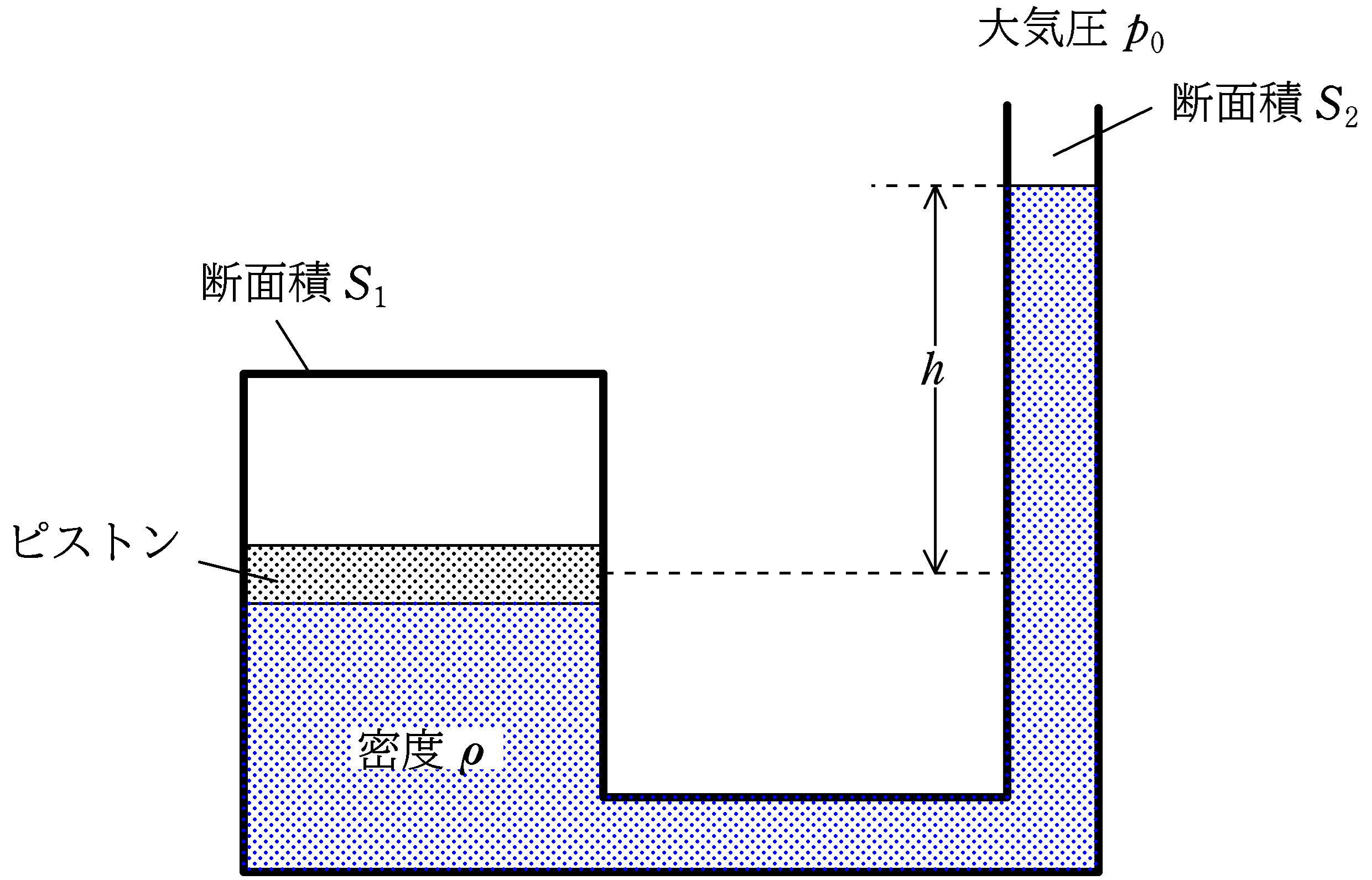
上図のように,断面積$S_{1}$で閉じられた部分と断面積$S_{2}$の開かれた部分からできている容器がある.断面積$S_{1}$の部分には厚さが無視できる質量$m$のピストンで封入されている.
また,ピストンの下側と断面積$S_{2}$の部分とそれをつなぐ部分には密度$\rho$の液体がある.
ピストンと断面積$S_{2}$の側の液面との高さの差は$h$である.大気圧を$p_{0}$とするとき,ピストンと容器の間に封入されている気体の圧力$P$を求めよ.
<解答>
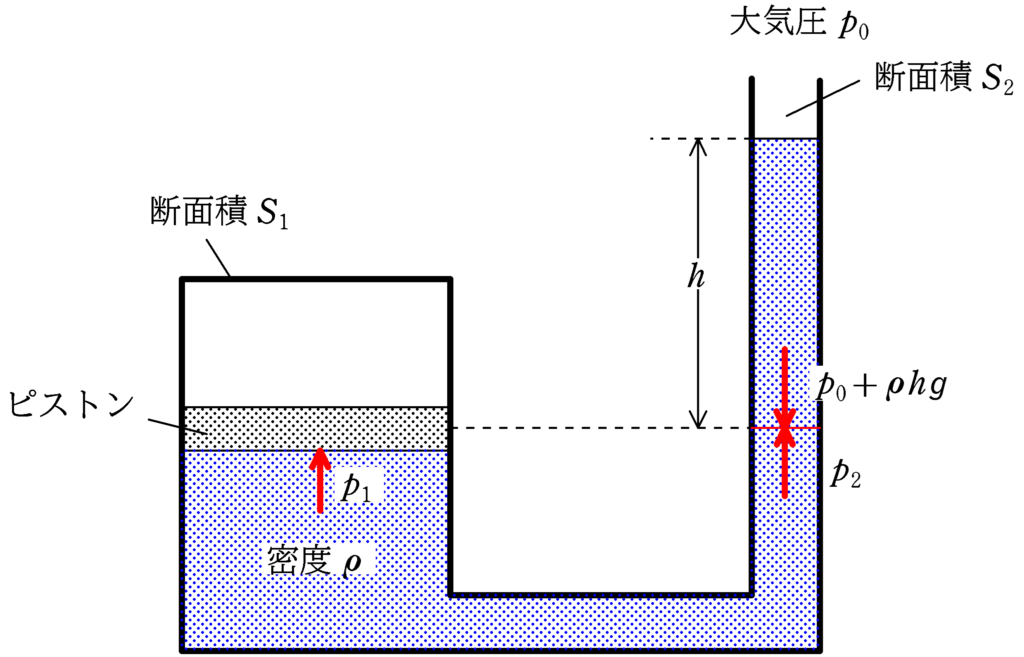

気体の圧力は,「可動部分のつり合いの式」で求めるのが基本です.
つまり,立てる式はピストンのつり合いの式です.
しかし,ピストンの下側の液体が押す力がわかりません.
そこで,深さが同じである.断面積$S_{1}$の部分の圧力のつり合いを考えます.
深さが$h$の部分の圧力は
$p_{0}+\rho hg$
なので,上図の$p_{2}$も
$p_{2}=p_{0}+\rho hg$
です.
すると,深さが同じである上図の$p_{1}$も同じ圧力です.すなわち
$p_{1}=p_{2}=p_{0}+\rho hg$
となります.
その上でピストンのつり合いの式を立てましょう.気体の圧力を$P$とします.
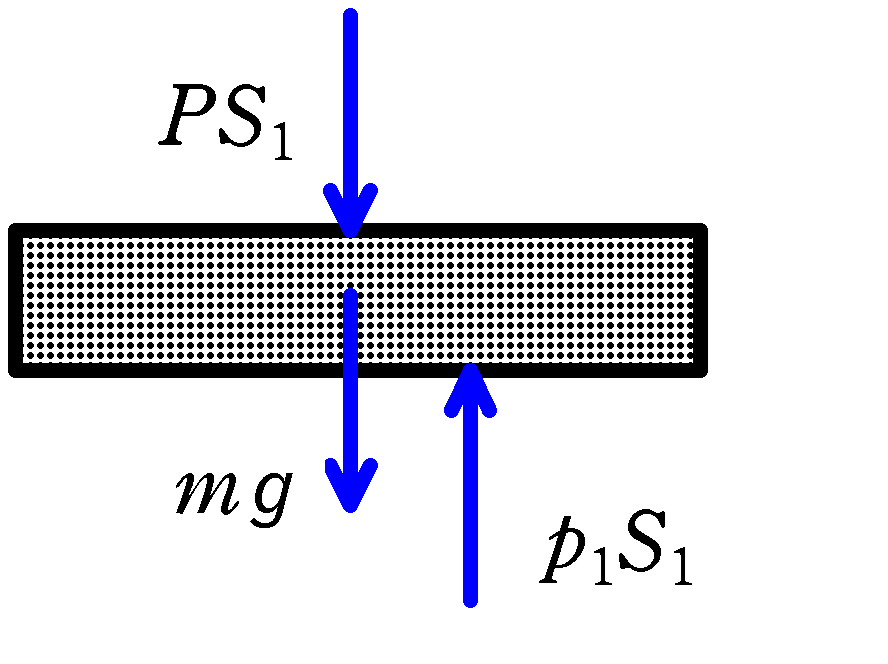
★ つり合いの式
\begin{align*} PS_{1}+mg&=p_{1}S_{1}\\ \therefore\,\,P&=p_{1}-\dfrac{mg}{S_{1}}\\ &=\textcolor{red}{p_{0}+\rho hg-\dfrac{mg}{S_{1}}}\,\,\textcolor{red}{(答)} \end{align*}


コメント