
今回は凹面鏡の式についてはなしです.
レンズの式と同様に,光源の位置,像の位置に関する式がないかを考えてみます.
前回の内容はこちら

光線の作図は以下の確認をしておいてください.
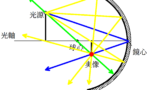
1. 鏡心にあたる光は,反射の法則にしたがって,反射する.
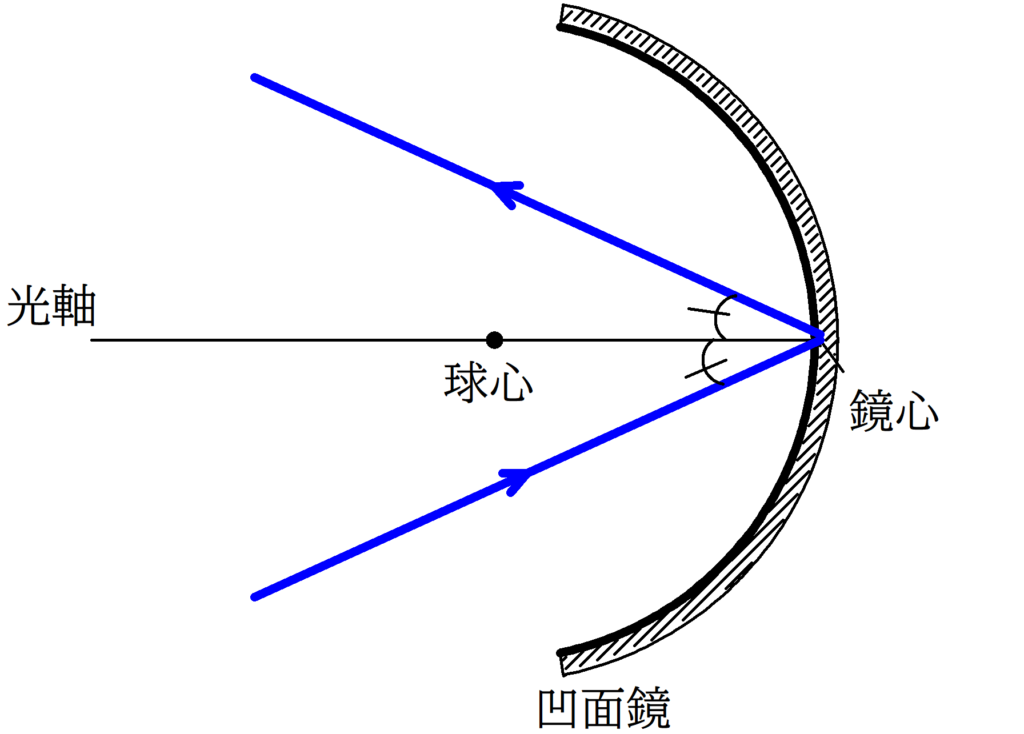
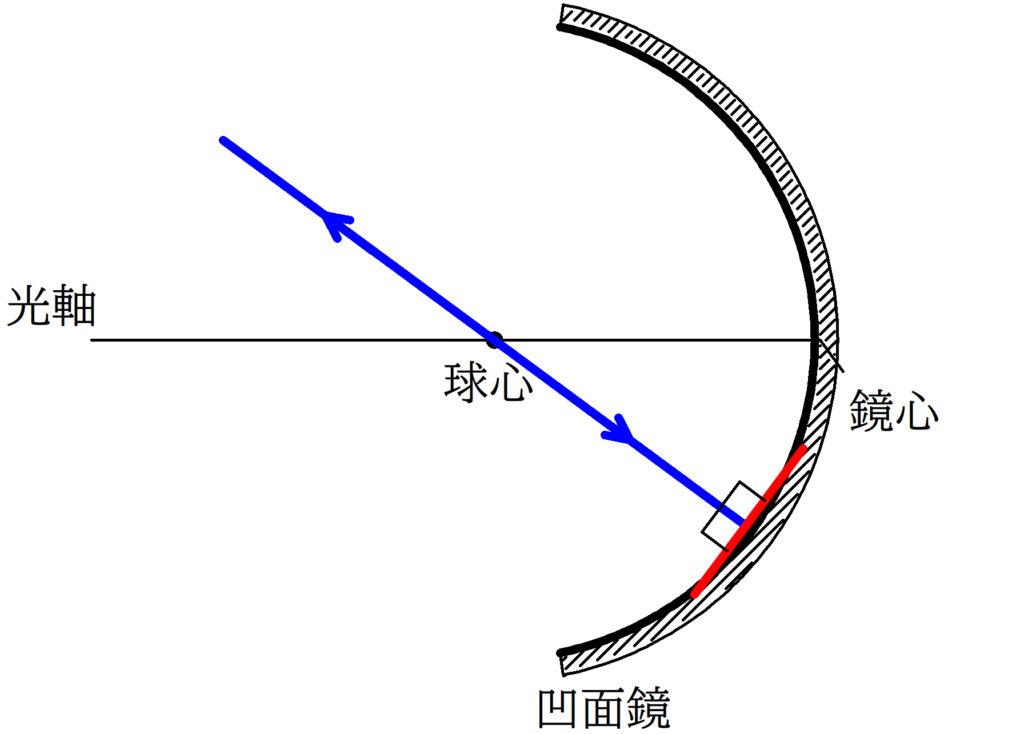
2. 球心を通る光線の入射角は90°なので,反射角も90°である.すなわち,反射光線は入射経路と同じ経路をたどる.
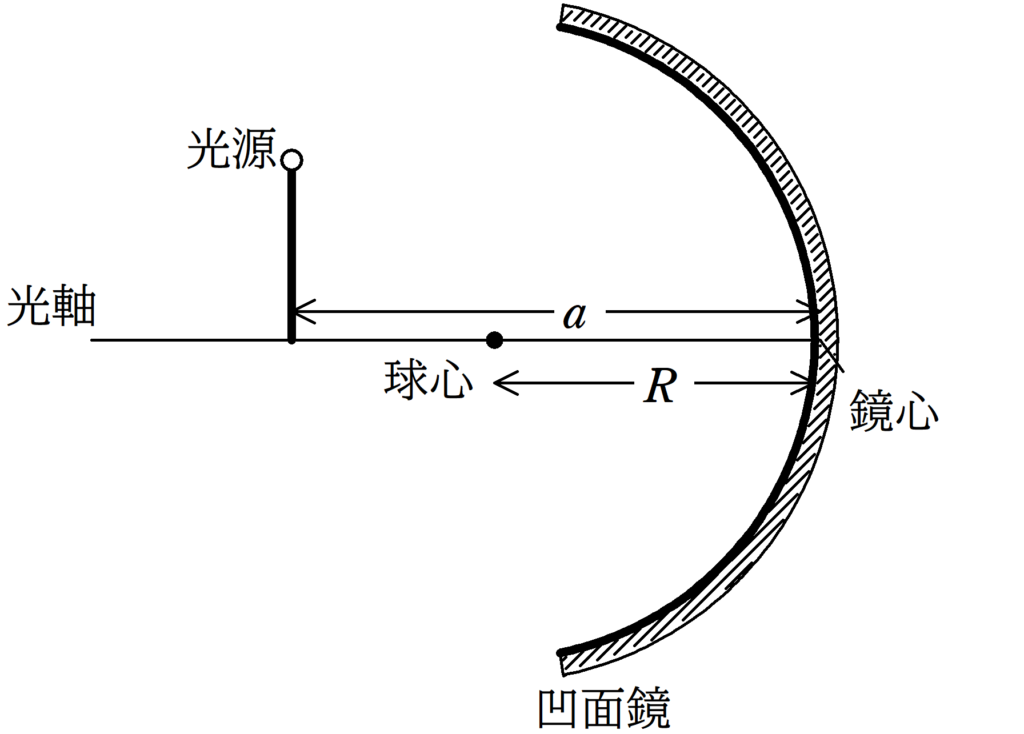
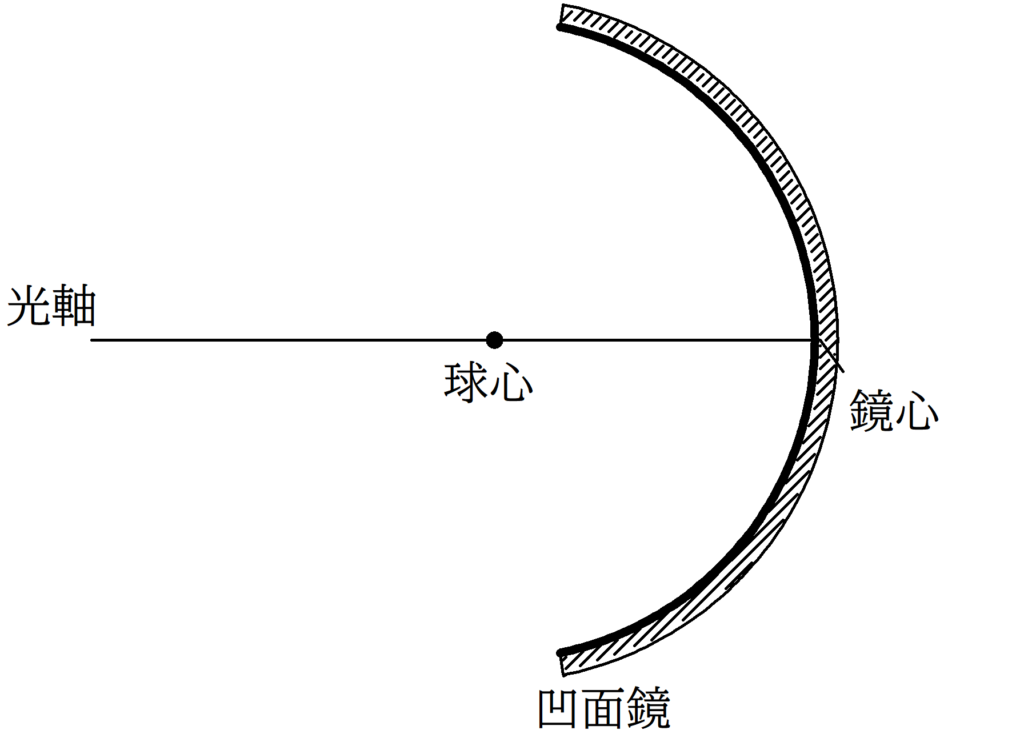
鏡心と光源との距離を$a$,凹面鏡の曲率半径を$R$,鏡心とできる像との距離を$b$とする.
以下の(1),(2)のそれぞれの場合について,$a$,$b$,$R$の関係式を導け.
(1)
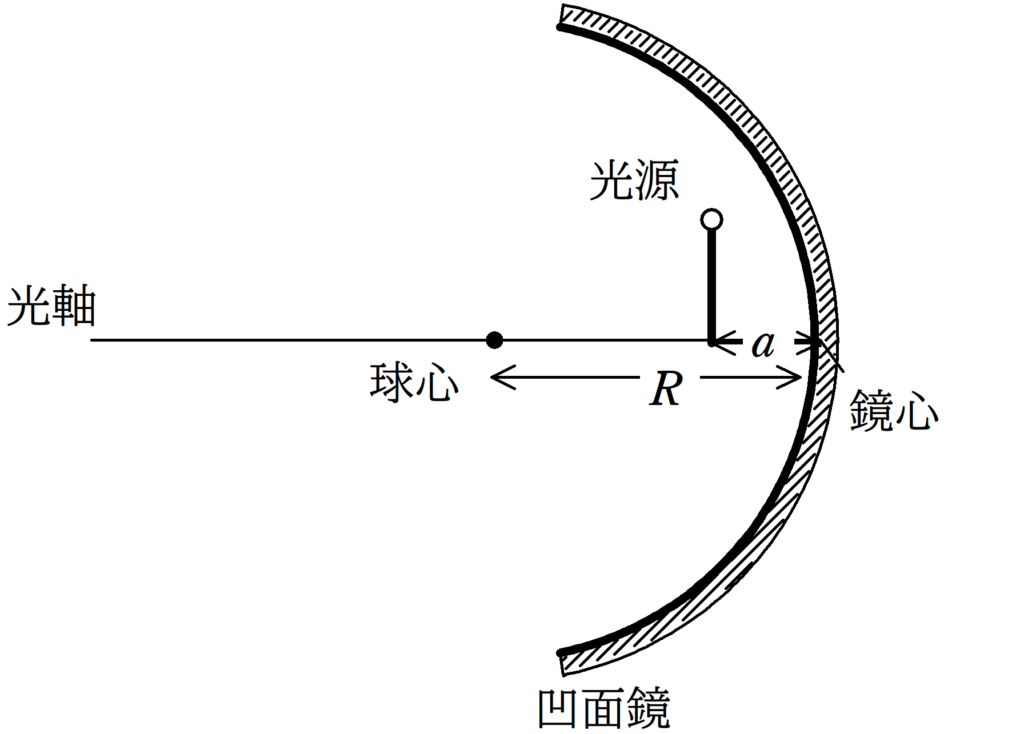
(2)
<解答>
(1)

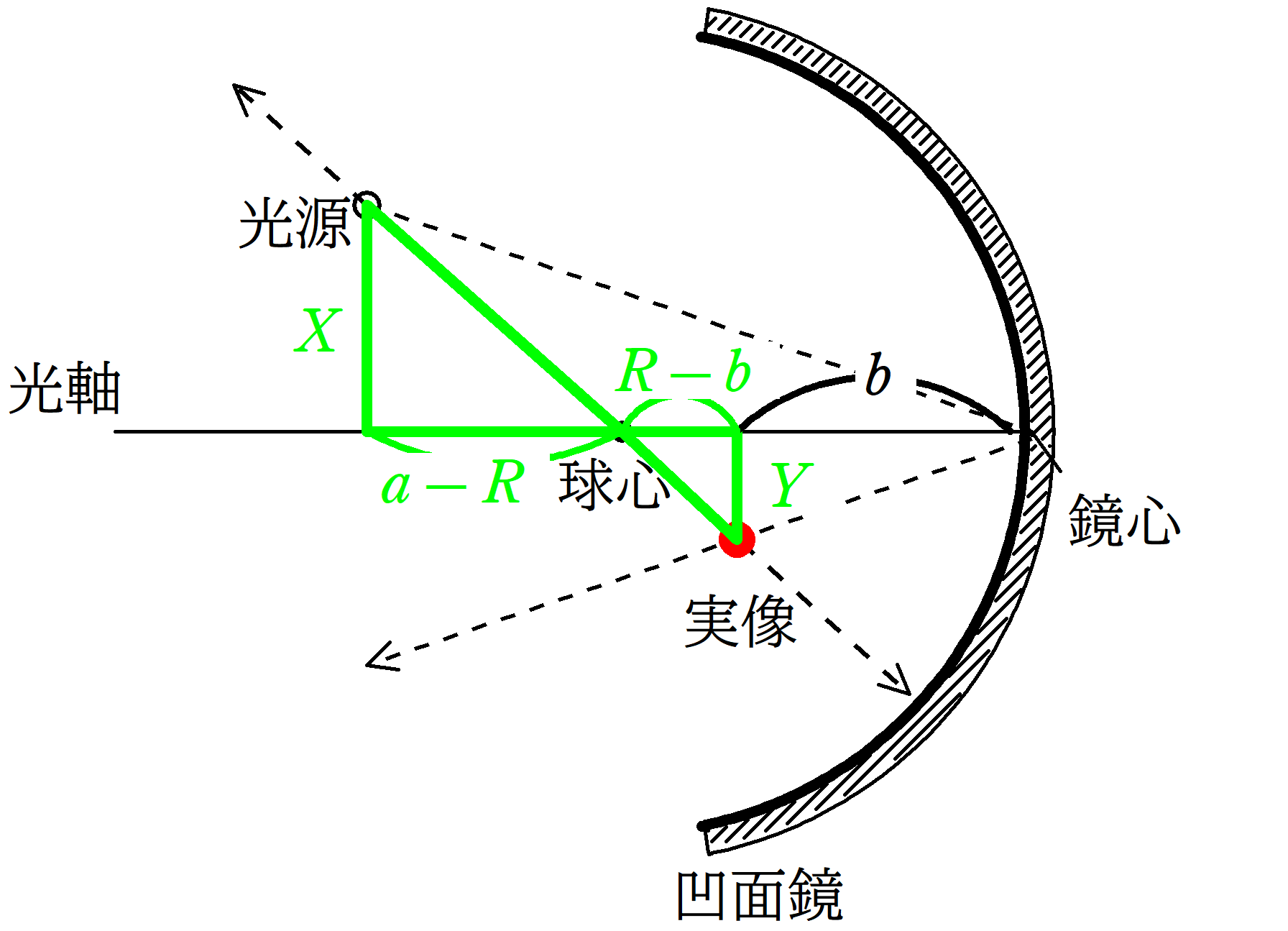
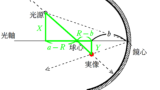
前回同様に代表光線をかきましょう.
①が鏡心にあたり,反射の法則にしたがって反射光線をかき,
②が球心を通り,入射角90°で凹面鏡に当たった後,反射角90°で反射した入射光線です.
その交点が赤い点になります.
すべての光線は赤い点を通って反射されていきます.
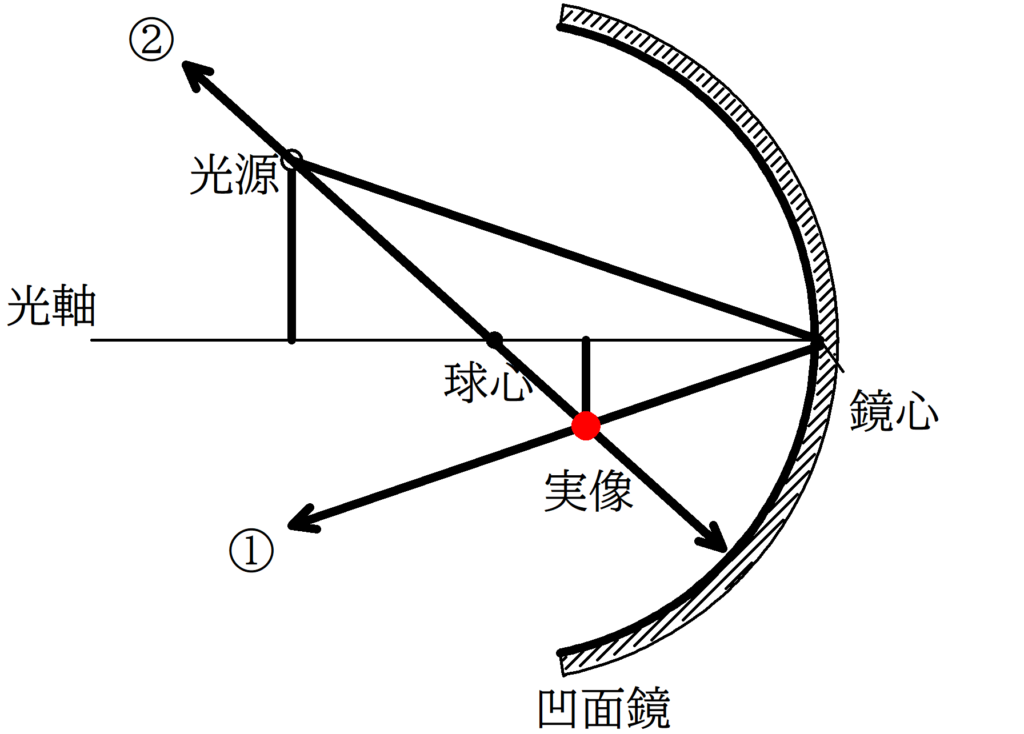

光源の高さを$X$,実像の高さを$Y$として相似な三角形を2つみつけ,相似比を考えていきましょう.
すると,次の2つの相似な図形がみつかるはずです.
赤い方の相似な図形はややみつけにくいので注意しましょう.
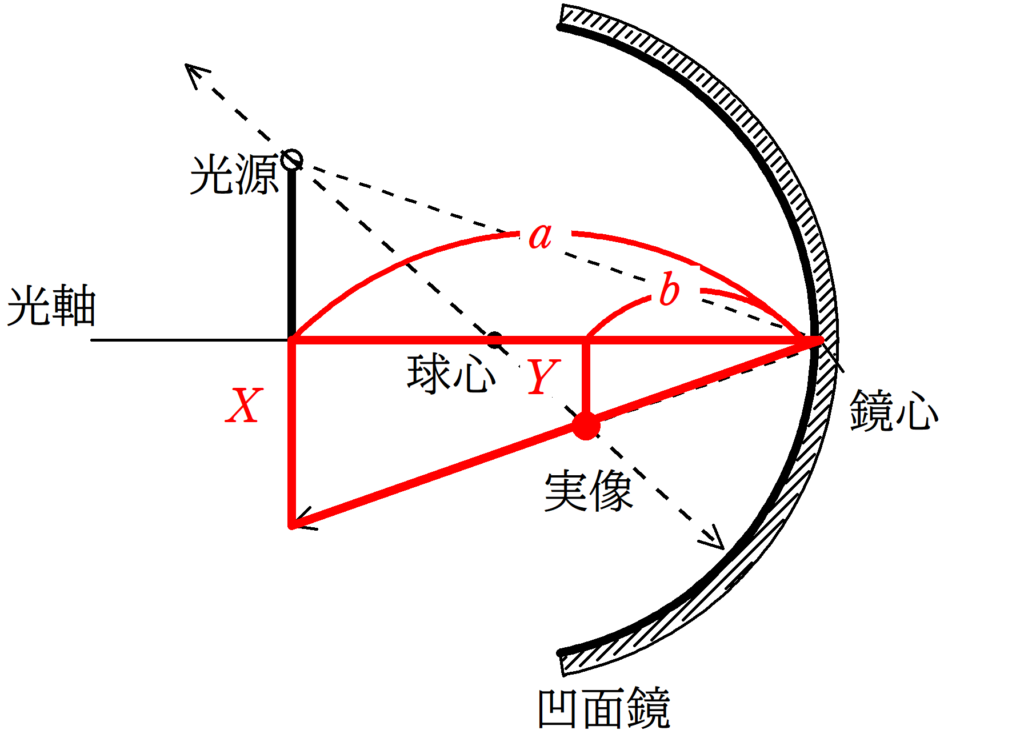
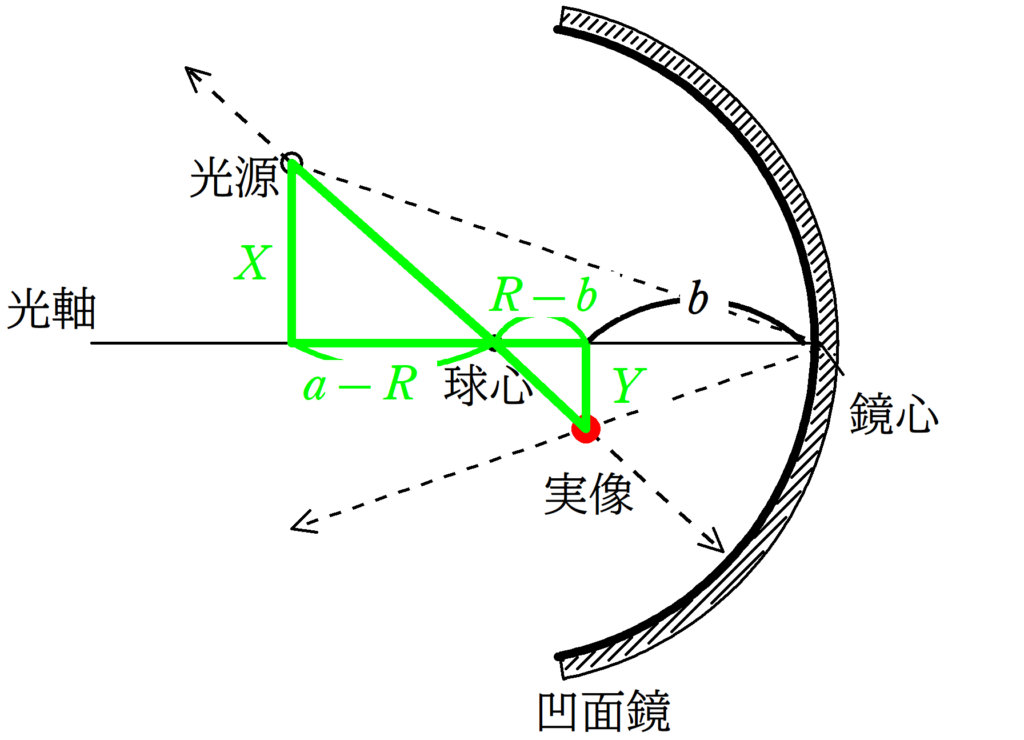
★ 赤い方の相似比
$\dfrac{Y}{X}=\dfrac{b}{a}$ $\dots (\ast)$
★ 緑の方の相似比
$\dfrac{Y}{X}=\dfrac{R-b}{a-R}$ $\dots (2\ast)$
$(\ast),(2\ast)$より
$\eqalign{\dfrac{b}{a}&=\dfrac{R-b}{a-R}\cr b(a-R)&=a(R-b)\cr ab-bR&=aR-ab \cr bR+aR&=2ab}$
両辺$abR$で割って
$\eqalign{\dfrac{bR}{abR}+\dfrac{aR}{abR}&=\dfrac{2ab}{abR}\cr \dfrac{1}{a}+\dfrac{1}{b}&=\dfrac{2}{R}}$

したがって,答えは$\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{2}{R}$です.

続いて,この凹面鏡の式から焦点の位置を考えていきましょう.
焦点は光軸に平行な光線が凹面鏡に反射して集まる場所と決めます.
光源を十分遠ざければ,光源から出た光線はほぼ光軸に平行な光線とみなすことができます.
その結果,すべての光は焦点に集まり,焦点の場所が実像の位置となります.

光源を十分遠くするから,$a\rightarrow \infty$として,このとき像は焦点の位置にできるから,鏡心からの焦点距離を$f$とすれば,$b\rightarrow f$ってことかな??

そういうことになります.
$a\rightarrow \infty$で$\dfrac{1}{a}\rightarrow 0$となるので,凹面鏡の式
$\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{2}{R}$
に代入すると次のようになります.
$0+\dfrac{1}{f}=\dfrac{2}{R}$
$\therefore f=\dfrac{R}{2}$

焦点は鏡心と球心の中点にあるんだね!
(2)

(2)も同様に
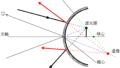
①:鏡心にあたる光線
②:球心にあたる光線
を考えます.
今度は,反射後に交じらないので,鏡の奥に交点を探します.
すべての光線は反射後,下図の赤い点から飛び出るように反射されるんだね!
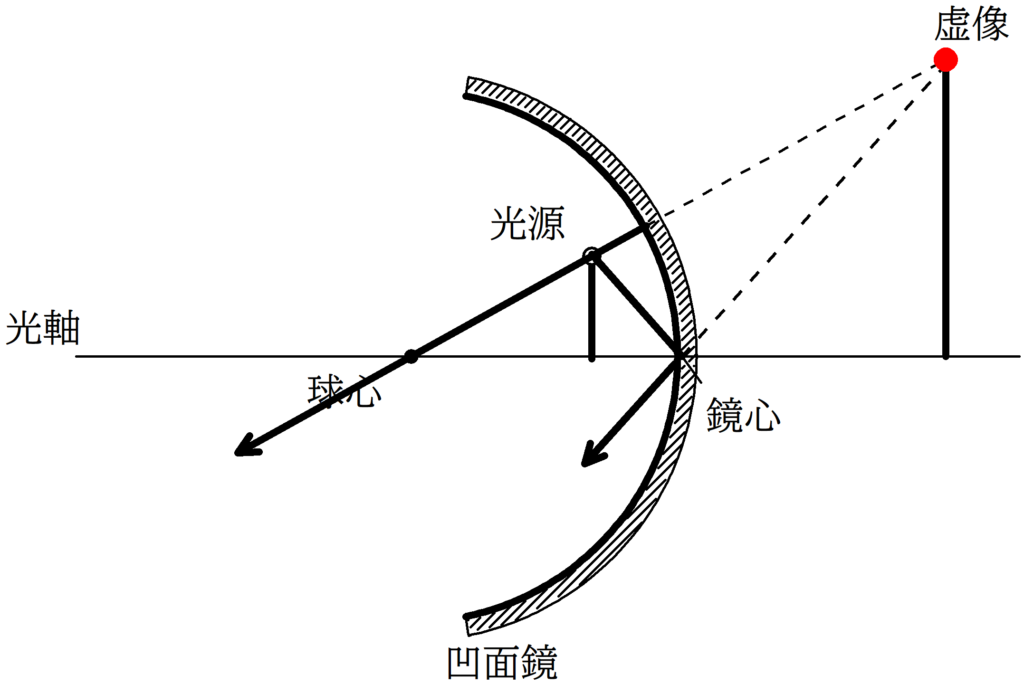

次に,光源の高さを$X$,虚像の高さを$Y$として,相似な図形を2組見つけて,相似比を考えます.
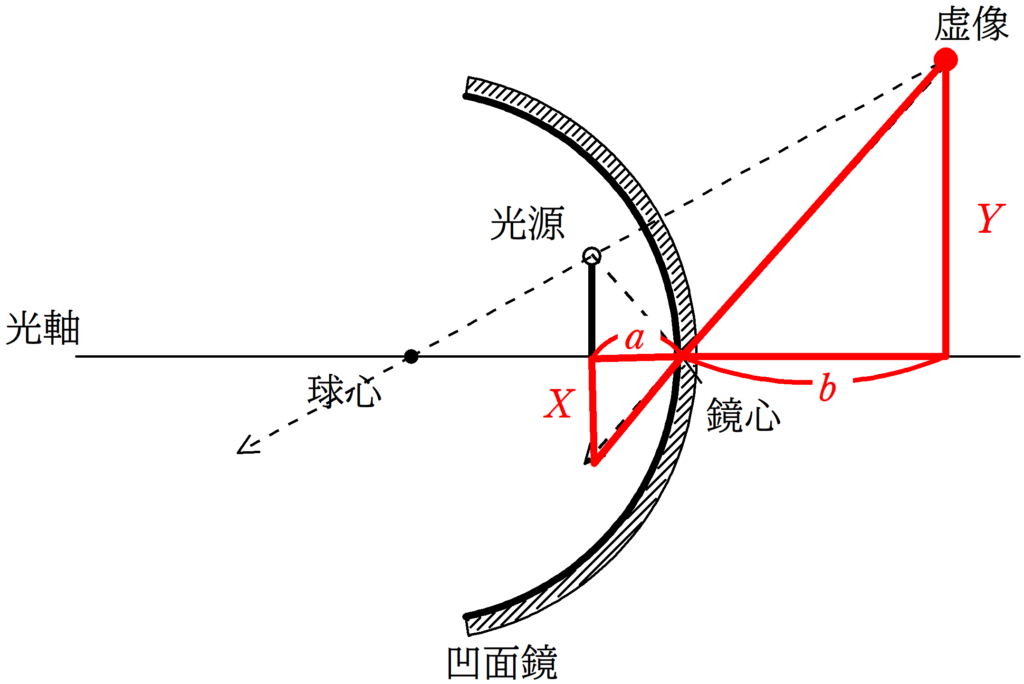
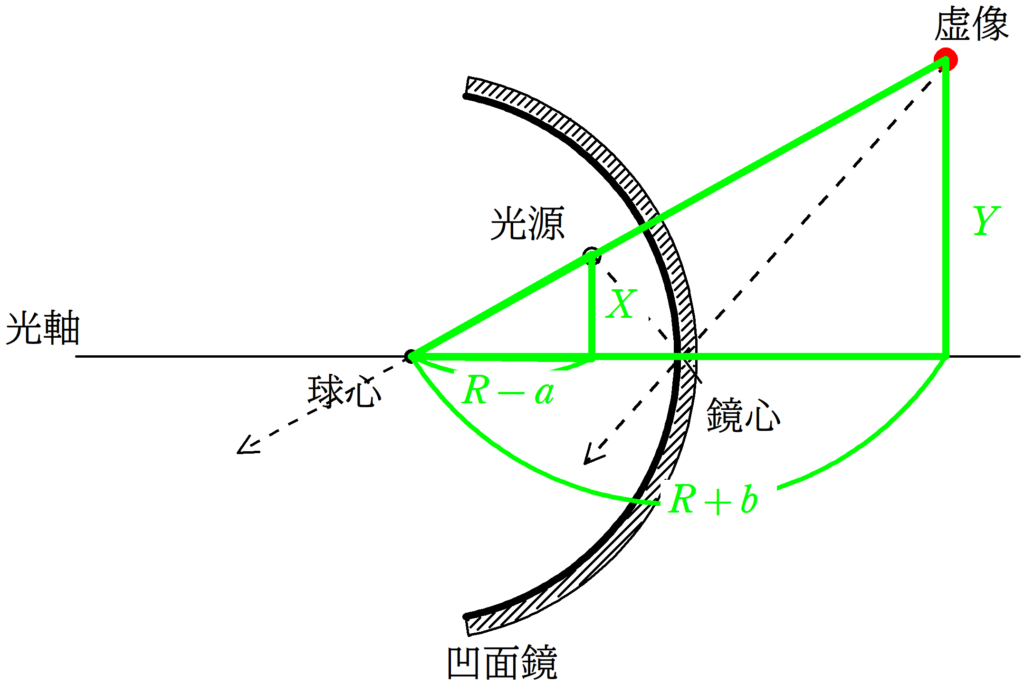
★ 赤い方の相似比
$\dfrac{Y}{X}=\dfrac{b}{a}$ $\dots (3\ast)$
★ 緑の方の相似比
$\dfrac{Y}{X}=\dfrac{R+b}{R-a}$ $\dots (4\ast)$
$(3\ast),(4\ast)$より
$\eqalign{\dfrac{b}{a}&=\dfrac{R+b}{R-a}\cr b(R-a)&=a(R+b)\cr bR-ab&=aR+ab \cr bR-aR&=2ab}$
両辺$abR$で割ると
$\dfrac{1}{a}-\dfrac{1}{b}=\dfrac{2}{R}$

虚像ができるから$-\dfrac{1}{b}<0$と考えることができるのかな.
同じように$a\rightarrow \infty$で$b\rightarrow f$とすると
$0-\dfrac{1}{f}=\dfrac{2}{R}$
となって,$f=-\dfrac{R}{2}$となるの??
なんかつじつまが合わないような・・・・

今回は,図としてかなり鏡心に近いときのことを考えているので,$a\rightarrow \infty$にするとつじつまが合わないのは当然です.
焦点を求めるのは(1)でやっているので,ここでは考えなくてもよいでしょう.
それでは,凹面鏡の式のまとめです.
鏡心から光源までの距離を$|a|$,鏡心からできる像までの距離を$|b|$,鏡心から焦点までの距離を$|f|$,曲率半径を$R$とすると,次の関係式が成り立つ.
$\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{2}{R}=\dfrac{1}{f}$
ただし,次の規則で正負を決める.
$b>0$ 実像ができるとき
$b<0$ 虚像ができるとき

次回の内容はこちらです.

コメント
[…] […]