
今回は,ベルトコンベア上の単振動の問題です.
ベルトコンベア上の単振動は一度,下の記事で扱っていますが,今回は少し難しい問題になっています.

何が違うの??

前回はずっと単振動をしてましたが,今回の問題は,単振動と等速度運動の組み合わせになります.
この問題の難しいところは,どのような運動をしているのかを把握するところですね.
ここは詳しくお話しましょう.
それでは,まず問題からみていきましょう.
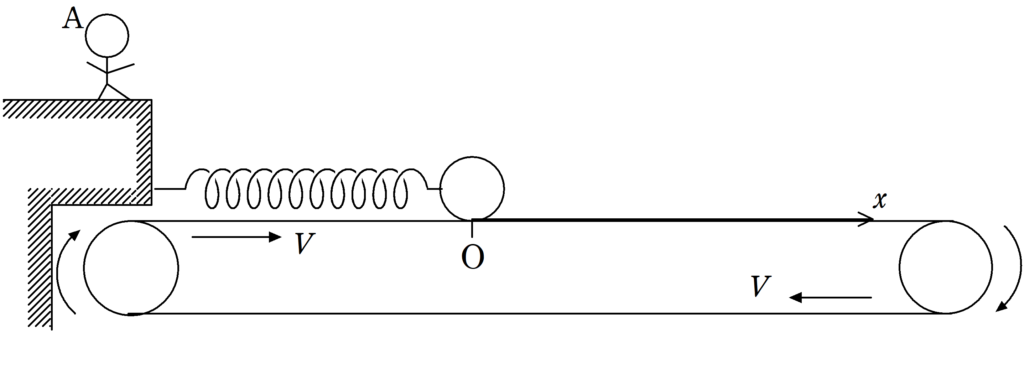
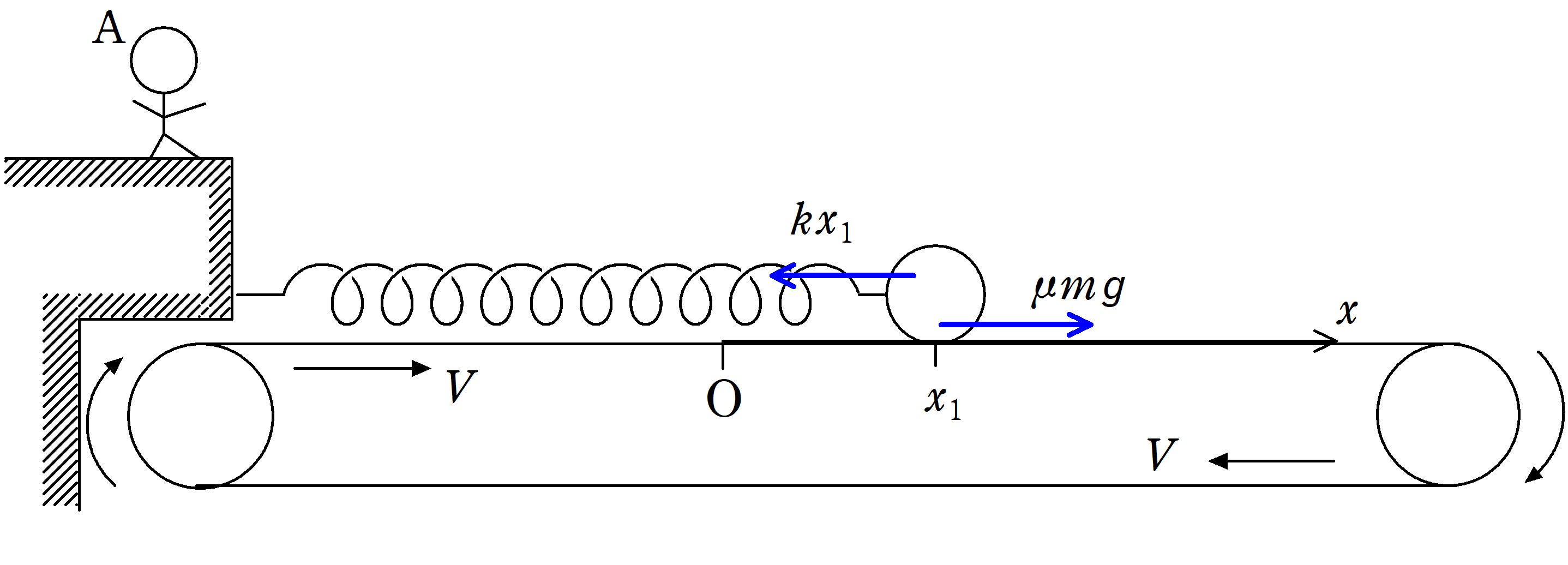
上図の向きにベルトコンベアが速さ$V$で動いている.
ベルトコンベアの上には,質量$m$の物体がおかれており,物体にはばね定数$k$のばねがつながれている.
ばねの他端は壁に固定されている.
壁の上には,静止した観測者Aがいる.
物体が自然長になる位置を原点として,ばねが伸びる向きに$x$軸をとる.
以下,ベルトコンベアの速さは十分小さく,ベルトコンベアと物体の間の静止摩擦係数と動摩擦係数をそれぞれ$\mu,\mu^{\prime}$($\mu >\mu^{\prime}$)とする.また,重力加速度の大きさを$g$とする.
(1) まず,物体を原点$\rm O$に静かにおいたところ,物体はベルトコンベアとともに右方向に速さ$V$で移動した.
しばらくすると,ある位置$x_{1}$で物体はすべりだした.このとき,$x_{1}$を$k , \mu , m , g$を用いて表せ.
(2) (1)の直後,観測者Aからみた物体の速度の向きは右向き,左向きどちらか.
(3) (1)の後,しばらく物体は単振動をした.
運動方程式を立てることで,振動の中心$x_{0}$,角振動数$\omega$,周期$T$を求めよ.
(4) 単振動の振幅を求めよ.
(5) 再びベルトコンベアに対して静止する位置$x_{2}$を求めよ.
<解答>
(1)

物体が右に移動していくと,ばねが伸びるから,弾性力がだんだんと大きくなっていくんだね.
それとともに,静止摩擦力も大きくなって,最大静止摩擦力になったところですべりだすだったね.
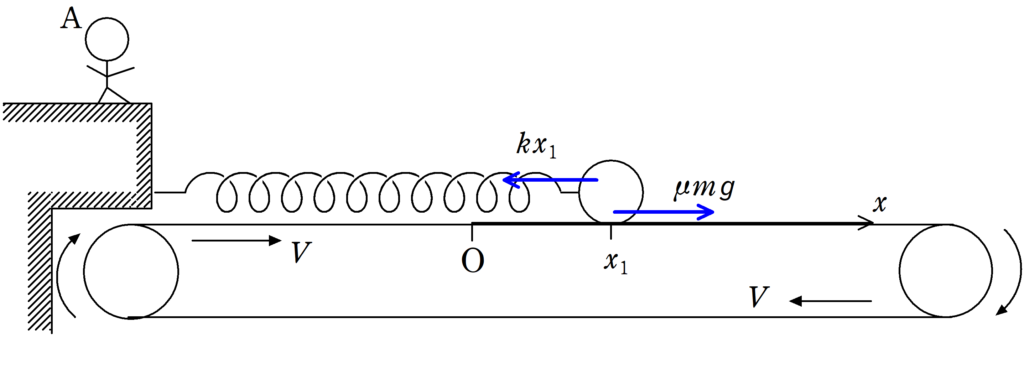
★ 物体にはたらく力のつり合いの式
弾性力と最大静止摩擦力のつり合いを考えて
$kx_{1}=\mu mg$ $\therefore$ $x_{1}=\dfrac{\mu mg}{k}$
(2)

(1)の直後は弾性力の方が大きくなるんだから,左向きに進むんじゃないの??

それは,よくある間違いです.
物体にはたらく力の合力と速度の向きは一致するとは限りません.

そうなの!?

たとえば,投げ上げ運動を思い出してください.
物体は常に鉛直下向きに重力を受けます.
しかし,鉛直上方向に速度を与えられるため,力の合力と速度の向きは一致していません.

たしかに!
そもそも,運動方程式$ma=F$から,力と関係するのは加速度なんだったね.

そういうことです.
力を加えると,その向きに加速します.

あれ?!
でも,物体は静止しているところからスタートするんだから,やっぱり左方向に力を受けて,左方向に加速して,その結果左向きに動くんじゃないの?

いえ,違います.
物体は静止していません.
ベルトコンベアとともに速さ$V$で右方向に移動しています.

そうだった!
あれ,でもなんで静止していると勘違いしたんだろう?

おそらく,弾性力と最大静止摩擦力のつり合いを考えたからでしょう.
静止摩擦力がはたらく原因は
ベルトコンベアに対して静止している
からです.
しかし,問題では,静止している観測者Aからみた運動を考えています.
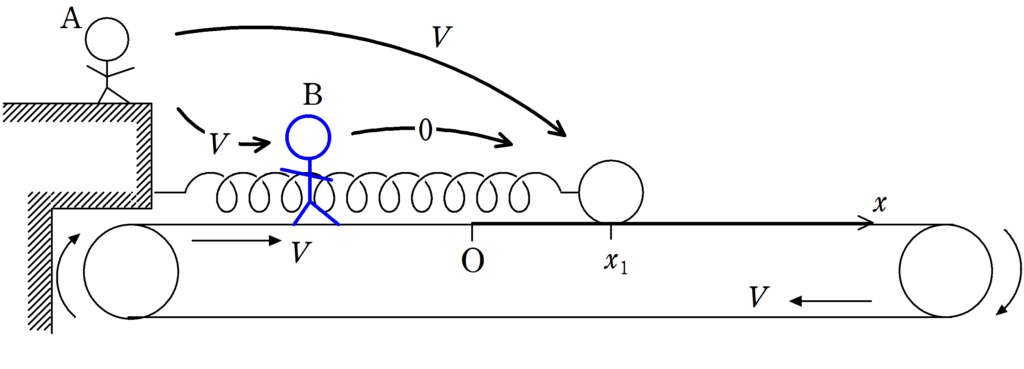
したがって,答えは右向き
(3)

(1)のあと,物体はベルトコンベアに対しては左向きに,静止した観測者からみたら右向きに速度をもちます.
動摩擦力は接触面からみたときの速度と反対向きにはたらきます.
したがって,動摩擦力の向きは,右方向です.
そして,静止した観測者からみて,単振動をはじめてから最初の方は物体は右方向に速度をもちます.

じゃあ,位置$x$における加速度を$a$として運動方程式を立てると,次のようになるね.
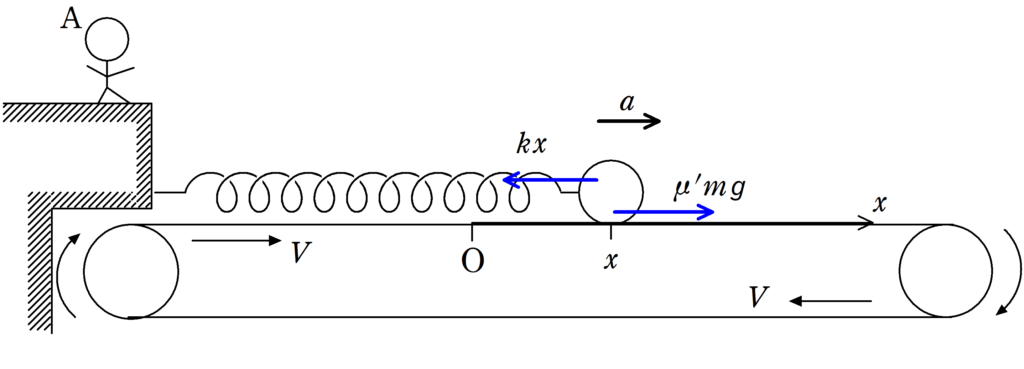
★ 物体の運動方程式
$\eqalign{ma&=\mu^{\prime}mg-kx\\&=-k(x-\dfrac{\mu^{\prime} mg}{k})}$
この運動方程式より
中心座標$x_{0}$は
$x_{0}=\dfrac{\mu^{\prime}mg}{k}$
角振動数は$\omega$
$\omega=\sqrt{\dfrac{k}{m}}$
周期$T$は
$T=\dfrac{2\pi}{\omega}=2\pi\sqrt{\dfrac{m}{k}}$
(4)

せっかく運動方程式を立てたので,振幅は単振動のエネルギー保存で求めましょう.
単振動のエネルギー保存は,中心からの距離を利用してくことに注意してね.
この式が使えない人は下の記事を読んでみて!
演習問題もあるよ.
単振動の運動方程式が
$ma=-k(x-x_{0})$
になるとき,単振動のエネルギー保存
$\dfrac{1}{2}mv^{2}+\dfrac{1}{2}k(x-x_{0})^{2}=$一定
が成り立つ.
※ $(x-x_{0})^{2}$は中心からの距離の2乗を表している.自然長からの距離ではない.
※ 上記の運動方程式を変形したものなので,摩擦力や重力がはたらいてもその仕事をいれないでよい.
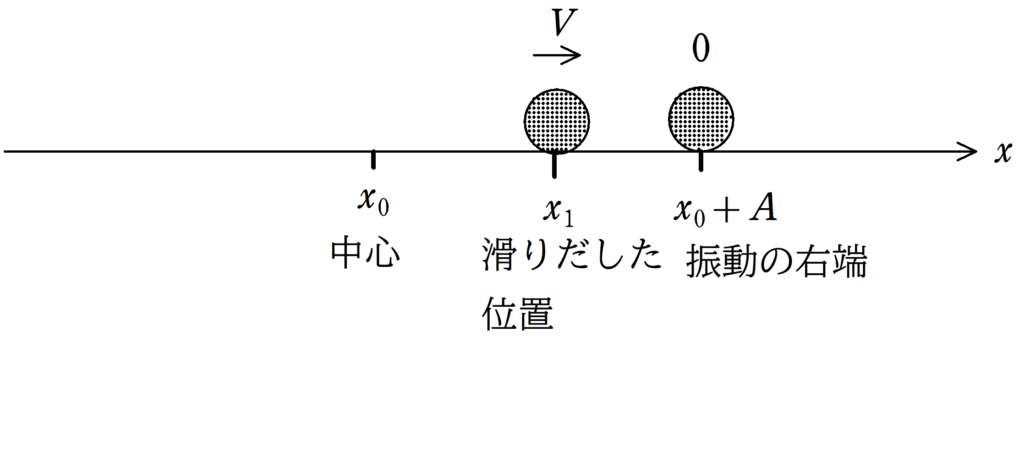

振幅を$A$としましょう.もちろん,$A>0$です.
すべりだしたときの中心からの距離は$x_{1}-x_{0}$,振動の右端の位置での中心からの距離は$A$ですね.
そして,それぞれの速さは$V$と$0$です.
したがって,単振動のエネルギー保存は次のようになります.
★ 単振動エネルギー保存
$\dfrac{1}{2}mV^{2}+\dfrac{1}{2}k(x_{1}-x_{0})^2=\dfrac{1}{2}m\cdot 0^{2}+\dfrac{1}{2}kA^2$
$x_{1}=\dfrac{\mu mg}{k}$,$x_{0}=\dfrac{\mu^{\prime} mg}{k}$より,
$\eqalign{A^{2}&=\dfrac{m}{k}V^{2}+(x_{1}-x_{0})^{2}\\ &=\dfrac{m}{k}V^{2}+(\dfrac{\mu mg}{k}-\dfrac{\mu^{\prime}mg}{k})^{2} \\ &=\dfrac{m}{k}V^{2}+(\dfrac{mg}{k})^{2}(\mu -\mu^{\prime})^{2} }$
$\therefore$ $A=\sqrt{\dfrac{m}{k}V^{2}+(\dfrac{mg}{k})^{2}(\mu -\mu^{\prime})^{2}}$
(5)

振動の右端に到達した後は動摩擦力の向きは変わるの??
もし変わるんだったら,運動方程式を立て直さなきゃだけど・・・

いえ,変わりません.
動摩擦力はベルトコンベアの上の人からみた相対速度の向きで決まるからです.
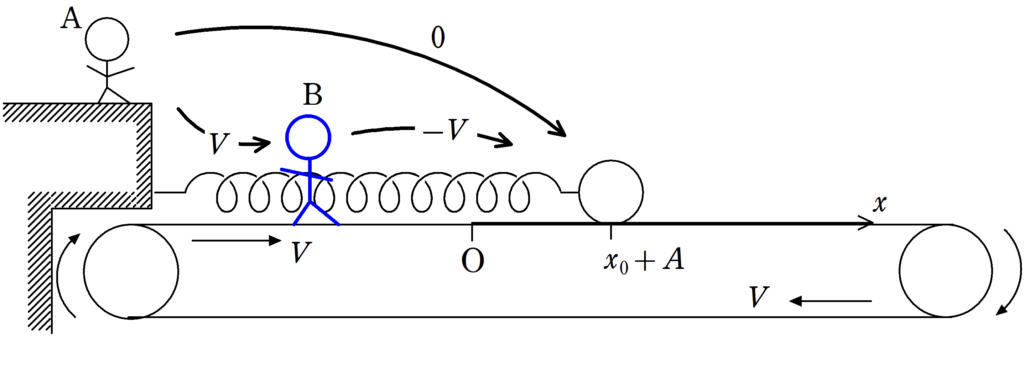

そうか,壁で静止しているAくんからみたら物体の速度は0だけど,ベルトコンベアに対して静止しているBくんからみると,物体は速度$-V$なんだね.
物体はBに対して左方向の速度をもっているから,動摩擦力は右向きのままなんだ.

そういうことになります.
そして,ベルトコンベアに対して静止するのは,ベルトコンベアに対し速度が0になったときです.

つまり,物体の速度が右向きに速さ$V$になったときだね.
単振動の対称性を利用すると,問題が簡単に解けそうかな.
ある物体の単振動について考える.
このとき,次のことが言える.
- 振動の中心からの距離が等しい2点での速さは等しい.
- 振動の中心からの距離が等しい2点での加速度の大きさは等しい.
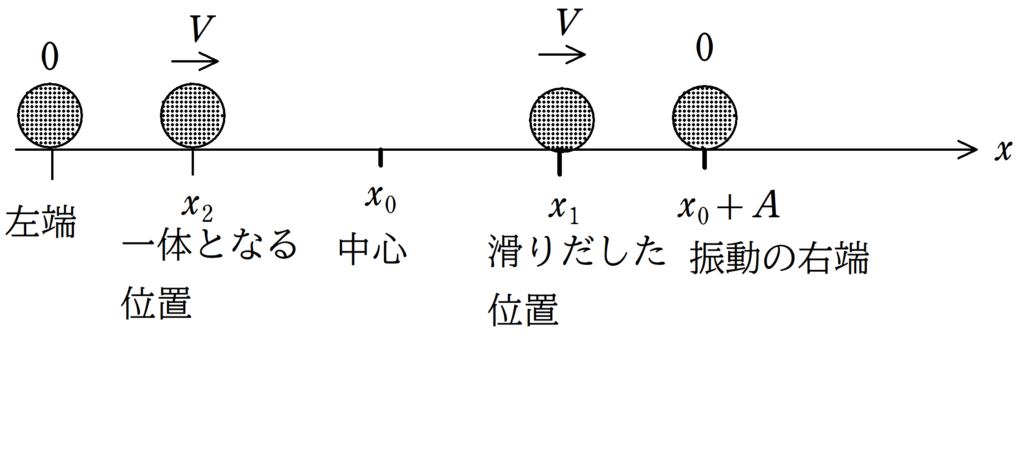
対称性を考えて,
$x_{0}=\dfrac{x_{1}+x_{2}}{2}$
$\therefore x_{2}=2x_{0}-x_{1}=\dfrac{mg}{k}(2\mu^{\prime}-\mu)$
答えは,$x_{2}=\dfrac{mg}{k}(2\mu^{\prime}-\mu)$

ちなみに,物体が$x=0$で静かにはなされた時刻を$t=0$とすると,物体の位置の時間変化は次のようになります.
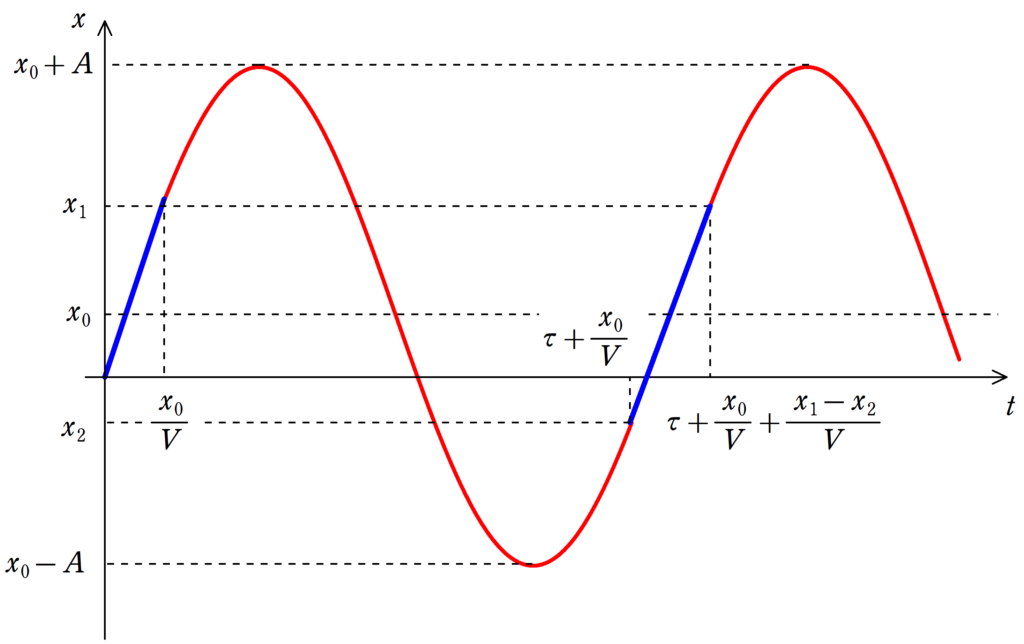

青い直線がベルトコンベアとともに運動しているときで,赤い曲線が単振動をしている部分です.単振動がはじまってから再びベルトコンベアと一体になるまでの時間を$\tau$としています.

結構難しかったね.
とくに,観測者が誰なのかを意識しないと解けないね.



コメント
とても参考になりました。
問題文6行目、ベルトコンベアの速さは十分小さいとありますが
十分大きいの間違いでしょうか?
いえ,「ベルトコンベア速さが十分に小さい」とすることで,ベルトコンベア上をすべっている物体が単振動をしたりベルトコンベアと一体となって移動したりする問題なので,これでOKです.逆に,「ベルトコンベアが速い」と,常に物体が単振動を続けることになります.このパターンは「https://physicmath.net/696/」にあります.