
今回は,次の2つの単振動を扱います.
- ベルトコンベア上の単振動
- 2つの回転棒によって引き起こされる単振動
まずは,ベルトコンベア上の単振動からです.
前回の内容はこちら
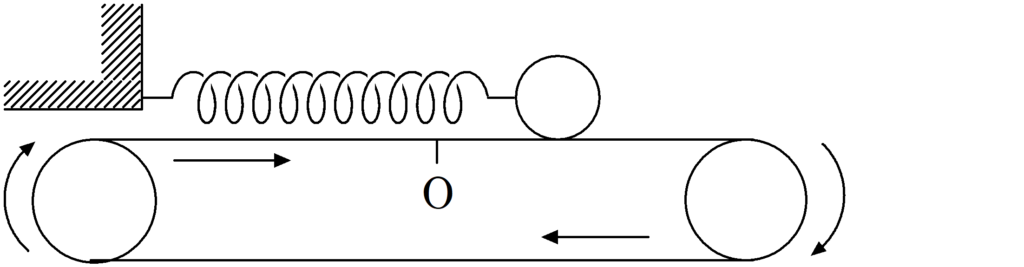
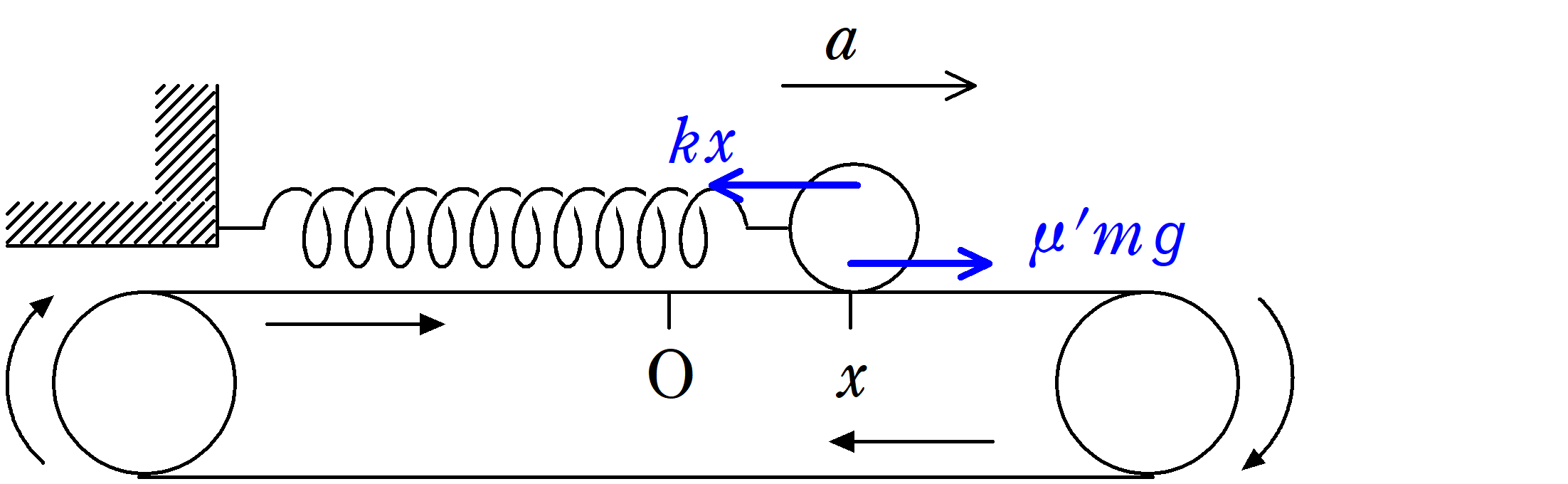
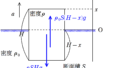
ばね定数$k$の軽いばねの一端は壁に固定され,他端は質量$m$の物体にとりつけられている.
ベルトコンベアは図の矢印の向きに一定の速さで運動している.
物体が自然長となる位置を原点として,ばねが伸びる方向に$x$軸をとる.
物体を原点にもってきて,静止する床に対する速度0でベルトコンベアにはなしたところ,物体は単振動をはじめた.
ただし,ベルトコンベアの速さは十分大きく,物体は常にベルトコンベア上を滑っているものとする.
また,重力加速度の大きさを$g$,ベルトコンベアと物体の間の動摩擦係数を$\mu^{\prime}$とする.
このとき,次の問いに答えよ.
(1) 振動の中心$x_{0}$,角振動数$\omega$,周期$T$を$m$,$k$,$g$,$\mu^{\prime}$から必要なものを用いて表せ.
(2) 物体をベルトコンベアにはなした時刻を$t=0$とする.
時刻$t$における物体の位置$x$を$m$,$k$,$g$,$\mu^{\prime}$,$t$から必要なものを用いて表せ.
<解答>
(1)
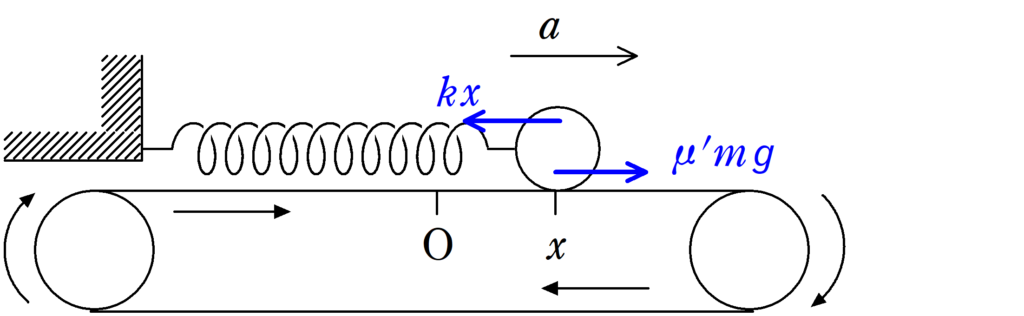
位置$x$における物体の加速度を$a$とします.
ベルトコンベアは十分速く,つねに図の左向き(進行する方向と反対方向)に摩擦力を受けるので,その反作用で物体はつねに右向きに摩擦力を受けます.
このように,物体にはたらく摩擦力の向きがわからない場合は,あえてベルトコンベアの摩擦力について考えてみるもの1つの手です.
したがって,物体の運動方程式は
$ma=-kx+\mu^{\prime}mg=-k\left(x-\dfrac{\mu^{\prime}mg}{k}\right)$
となります.
この運動方程式から中心座標は
$x_{0}=\dfrac{\mu^{\prime}mg}{k}$
角振動数は
$\omega=\sqrt{\dfrac{k}{m}}$
周期は
$T=2\pi \sqrt{\dfrac{m}{k}}$
となります.
(2)
$x=0$で速度が0なのでここが振動の端っこです.
また,振動の中心が$x_{0}=\dfrac{\mu^{\prime}mg}{k}$なので,$x=0$が左端であることがわかります.
したがって,左端から中心までの距離である振幅$A$は$A=\dfrac{\mu^{\prime}mg}{k}$となります.
また,最小の場所から$x$軸の正の方向へスタートするので,$-\cos$型ですね.
これらのことから,時刻$t$における物体の位置$x$は
$x=x_{0}-A\cos \omega t=\dfrac{\mu^{\prime}mg}{k}-\dfrac{\mu^{\prime}mg}{k} \cos \omega t$
となります.
摩擦力の向きさえわかれば,いままでと同様に解ける問題でした.

続いて,回転棒が単振動を引き起こす問題です.次は力のモーメントのつり合いを利用します.
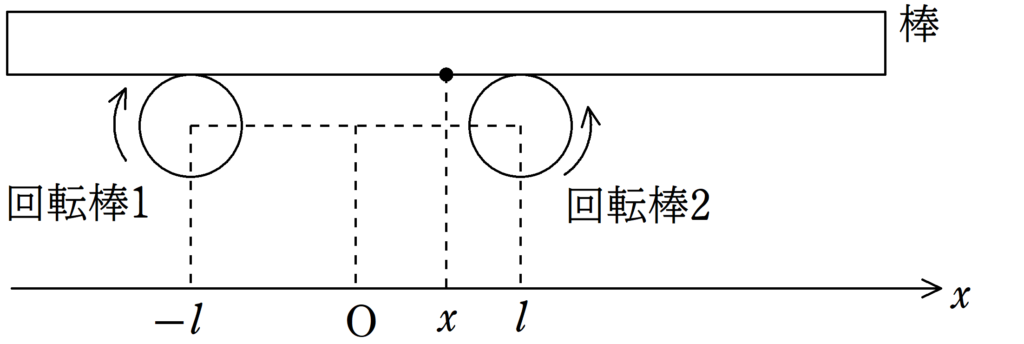
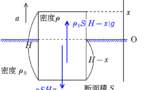
回転棒1と回転棒2が上図の向きに一定の角速度で回転している.
2つの回転棒の上に質量$m$の棒をおくと,棒は水平になる.
回転棒1の中心の座標を$x=-l$,回転棒2の中心の座標を$x=l$,2つの回転棒の中心の中点を$x=0$とする.
棒は一様な密度で,その重心の位置を$x$とする.
2つの回転棒が回転している状態で,棒の重心を$x=L_{0} (0<L_{0}<l)$となる位置に静止する床に対して速度0となるようにおいたところ棒は単振動をはじめた.
次の問いに答えよ.
ただし,回転棒1 , 2と棒の間の動摩擦係数を$\mu$,重力加速度の大きさを$g$とする.
(1) 棒の重心から$x$の位置にあるときを考える.
このとき,棒と回転棒1の間にはたらく垂直抗力の大きさを$N_{1}$,棒と回転棒2の間にはたらく垂直抗力の大きさを$N_{2}$とする.
力のモーメントのつり合いの式を利用して,$N_{1}$,$N_{2}$を$l$,$x$,$m$,$g$を用いて表せ.
(2) 棒の単振動の中心座標$x_{0}$,角振動数$\omega$,周期$T$を$l$,$\mu$,$g$を用いて表せ.
(3) 棒をはなした時刻を$t=0$とする
.時刻$t$における棒の重心の位置$x$を,$L_{0}$,$\mu$,$g$,$l$,$t$を用いて表せ.
<解答>
(1)
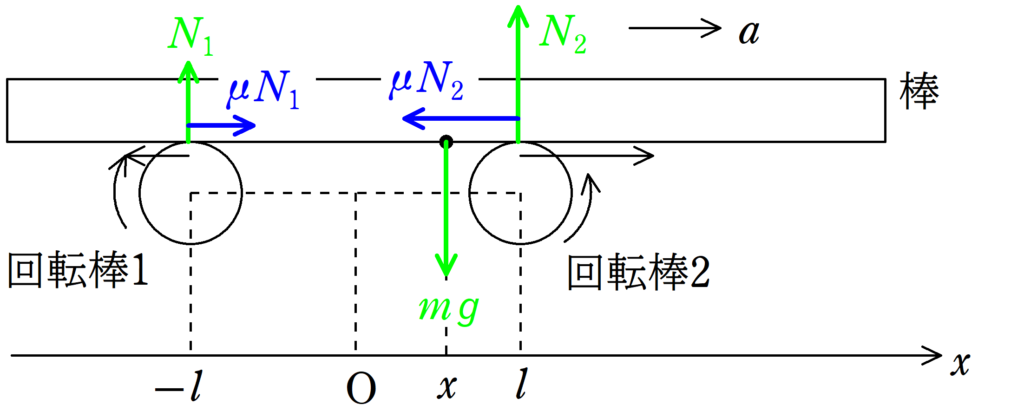
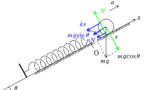
棒の重心が$x$であるときに棒にはたらく力を図示すると上図のようになります.
回転棒2と棒の間の垂直抗力がはたらく場所をモーメントの中心とすると,棒にはたらく重力$mg$は反時計回りのモーメントでその大きさは$(l-x)mg$であり,$N_{1}$は時計回りのモーメントでその大きさは$2lN_{1}$となります.
力のモーメントのつり合いの式より
$(l-x)mg-2lN_{1}=0$ $\therefore$ $N_{1}=\dfrac{l-x}{2l}mg$
また,回転棒1と棒の間の垂直抗力がはたらく場所をモーメントの中心とすると,棒にはたらく重力$mg$は時計回りのモーメントでその大きさは$(x+l)mg$であり,$N_{2}$は反時計回りのモーメントでその大きさは$2lN_{2}$となります.
力のモーメントのつり合いの式より
$2lN_{2}-(x+l)mg=0$ $\therefore$ $N_{2}=\dfrac{l+x}{2l}mg$
(2)
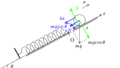
次に,棒の水平成分の運動を考えます.
棒の重心が$x$にあるときの棒の加速度を$a$とします.
回転棒1は棒との接触部分の場所で左方向に摩擦力を受けているので,その反作用で棒は右方向に動摩擦力$\mu N_{1}$を受けています.
同様に,回転棒2は棒との接触部分の場所で右方向に摩擦力を受けているので,その反作用で棒は左方向に動摩擦力$\mu N_{2}$を受けます.
動摩擦力は$\mu mg$ではありません,注意です.
すると,運動方程式は
$\eqalign{ma&=\mu N_{1}-\mu N_{2} \\&=\mu \dfrac{l-x}{2l}mg-\mu \dfrac{l+x}{2l}mg\\&=-\dfrac{\mu mg}{l}x}$
この運動方程式より,中心座標は$x_{0}=0$,角振動数は$\omega=\sqrt{\dfrac{\mu g}{l}}$,周期は$T=2\pi \sqrt{\dfrac{l}{\mu g}}$となります.
(3)
(2)より中心座標がわかりました.
問題では$x=L_{0}$からスタートし,この場所は速度が0なので,振動の右端となります.
振動の右端と中心までの距離が振幅$A$なので,$A=L_{0}$です.
また,右端(最高点)から$x$軸の負の向きにスタートするので$\cos$型ですね.
したがって,時刻$t$における棒の重心の位置$x$は
$x=x_{0}+A\cos \omega t=L_{0} \cos \sqrt{\dfrac{\mu g}{l}}t$

このように,ばねがなくても単振動をするのがわかります.
ここまでくると,運動方程式を立てないと先へ進めません.
運動方程式をたてることが大事なんだと実感できる問題ですね.
次回は[基本編]の最後です.
次回の記事はこちら

コメント
[…] 物理 Twitter Facebook はてブ Pocket LINE コピー 2020.08.28 [基本]単振動の演習問題⑨ 運動方程式を立てる5今回は,次の2つの単振動… […]
[…] [基本]単振動の演習問題⑨ 運動方程式を立てる5今回は,次の2つの単振動… […]
[…] [基本]単振動の演習問題⑨ 運動方程式を立てる5PHYさん今回は,次の2つの… […]
[…] [基本]単振動の演習問題⑨ 運動方程式を立てる5PHYさん今回は,次の2つの… NEKO […]