<問題>
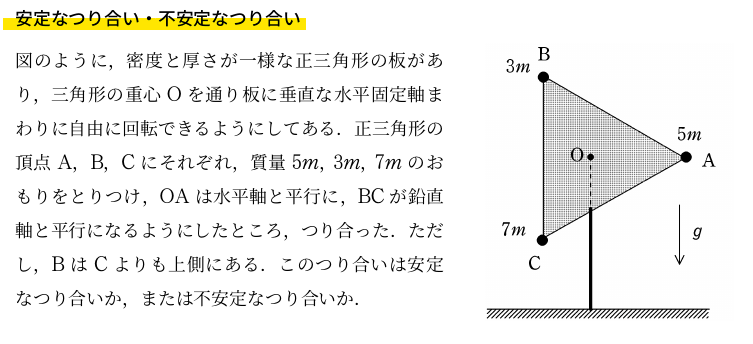
<解答>
「安定なつり合い・不安定なつり合い」の問題はこちらもあります.
つり合いの位置から少しずらしても元に戻る状態を「安定なつり合い」といい,つり合いの位置から少しずらすと大きく離れてしまう状態を「不安定なつり合い」という.
つり合いの位置から少しずらしたときを考えてみる.具体的には,AにあるおもりをOまわりに微小角度$\theta$だけ回転したときのOまわりの力のモーメントを考える.
反時計回りを力のモーメントの正の向きとしたとき,力のモーメントの和が正であれば,よりもとの位置から離れてしまうので不安定なつり合いだし,力のモーメントの和が負であれば,元の位置にもどるので安定なつり合いである.
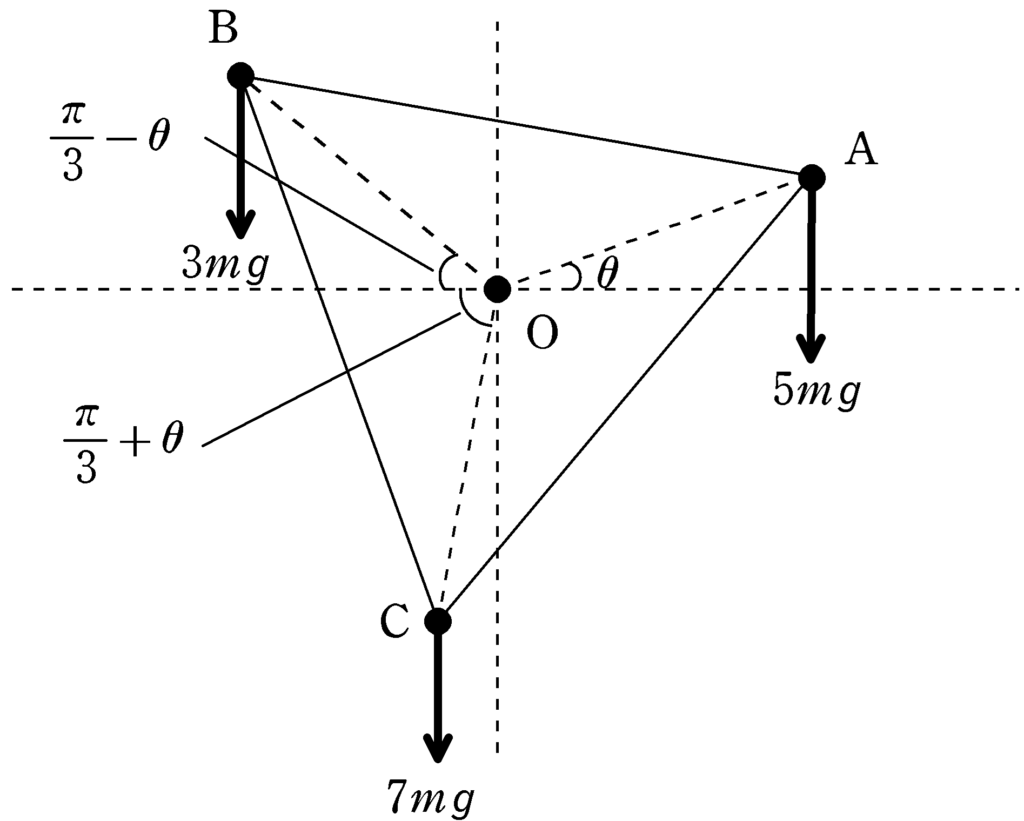
Aを反時計回りに微小角度$\theta$回転させると,B・Cの水平方向からの角度は上図のように$\dfrac{\pi}{3}-\theta,\dfrac{\pi}{3}+\theta$となる.(ただし,それぞれの角度が90度未満になる方の角度をとっている)
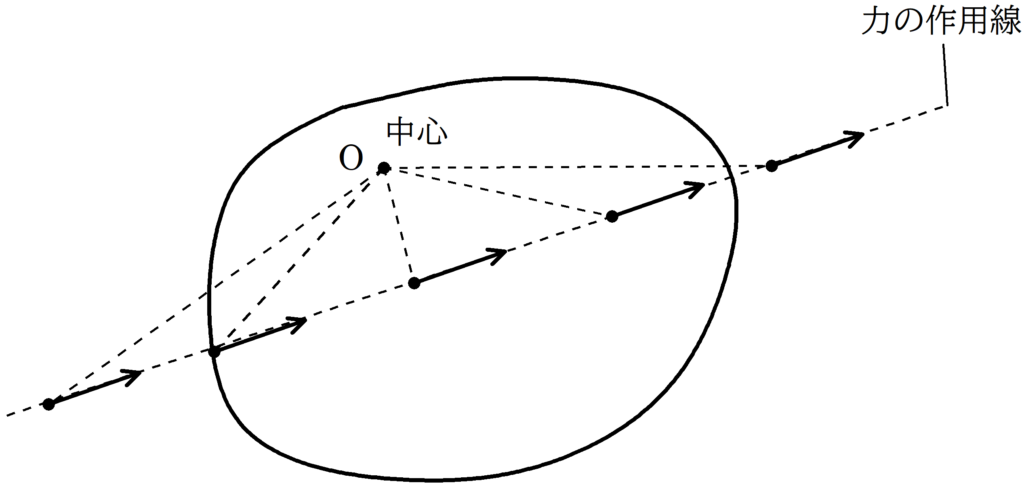
このままOまわりの力のモーメントの和を計算するのは大変そうなので,「作用線平行移動の原理」を用いる.(詳しい説明はこちら)
中心を$\rm O$とし,ある始点にはたらく力のモーメントを計算するとき,力の作用線上のどこに移動させても力のモーメントは同じである.
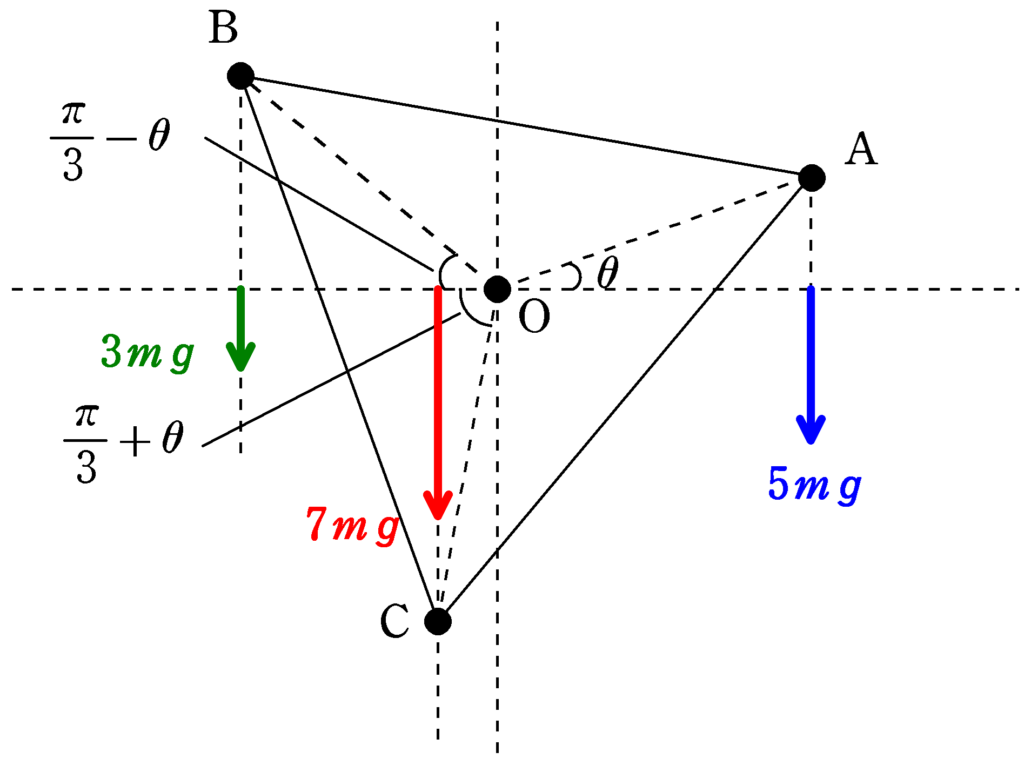
上のように,Oを通って水平な軸まで力の始点を移動すると簡単に計算できる.${\rm OA=OB=OC}=L$とすると,
${\rm OA}=L\cos\theta$
${\rm OB}=L\cos\left(\dfrac{\pi}{3}-\theta\right)$
${\rm OC}=L\cos\left(\dfrac{\pi}{3}+\theta\right)$
となる.
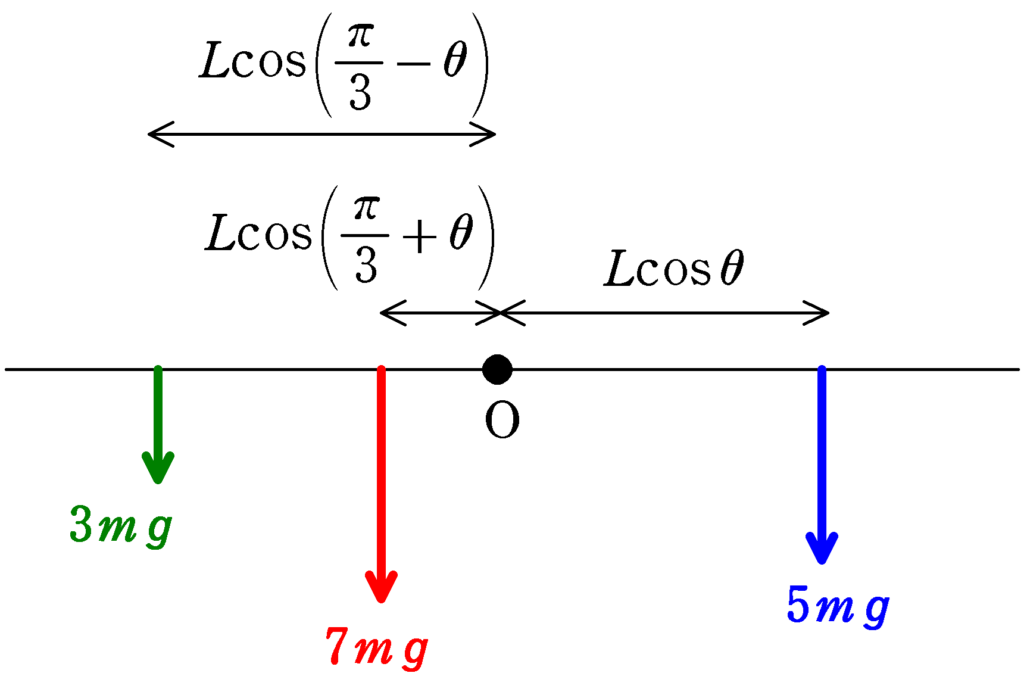
Oを中心とし,反時計回りを正とする.$5mg$の力は時計回りなので,力のモーメントは負.$3mg,7mg$は反時計回りなので,力のモーメントは正である.力のモーメントの和を$N$とすると
$\eqalign{N&=3mg\times L\cos\left(\dfrac{\pi}{3}-\theta\right)+7mg\times \cos\left(\dfrac{\pi}{3}+\theta\right)-5mg\times L\cos\theta\\&=mgL\left\{3\cos\left(\dfrac{\pi}{3}-\theta\right)+7\cos\left(\dfrac{\pi}{3}+\theta\right)-5\cos\theta\right\}}$
$N$の正負を知りたいだけなので,$3\cos\left(\dfrac{\pi}{3}-\theta\right)+7\cos\left(\dfrac{\pi}{3}+\theta\right)-5\cos\theta \cdots (\ast)$だけに着目する.
加法定理で展開すると
$\eqalign{\cos\left(\dfrac{\pi}{3}-\theta\right)&=\cos\dfrac{\pi}{3}\cos\theta+\sin\dfrac{\pi}{3}\sin\theta\\&=\dfrac{1}{2}\cos\theta+\dfrac{\sqrt{3}}{2}\sin\theta}$
$\eqalign{\cos\left(\dfrac{\pi}{3}+\theta\right)&=\cos\dfrac{\pi}{3}\cos\theta-\sin\dfrac{\pi}{3}\sin\theta\\&=\dfrac{1}{2}\cos\theta-\dfrac{\sqrt{3}}{2}\sin\theta}$
したがって,$(\ast)$は
$\eqalign{(\ast)&=3\left(\dfrac{1}{2}\cos\theta+\dfrac{\sqrt{3}}{2}\sin\theta\right)+7\left(\dfrac{1}{2}\cos\theta-\dfrac{\sqrt{3}}{2}\sin\theta\right)-5\cos\theta\\&=-2\sqrt{3}\sin\theta\,\,<0}$
力のモーメントの和が負なので,Aを反時計回りに少しだけ回転させると,元の位置にもどろうとする.
一方,$\theta\to -\theta$(時計回りに少しだけ回転させるとき)とすると,力のモーメントの和は
$-2\sqrt{3}\sin(-\theta)=2\sqrt{3}\sin\theta\,\,>0$
より,力のモーメントは正.反時計回りに少しだけ回転させると,やはりもとにもどろうとする.
以上から,この問題の答えは安定なつり合い(答)



コメント