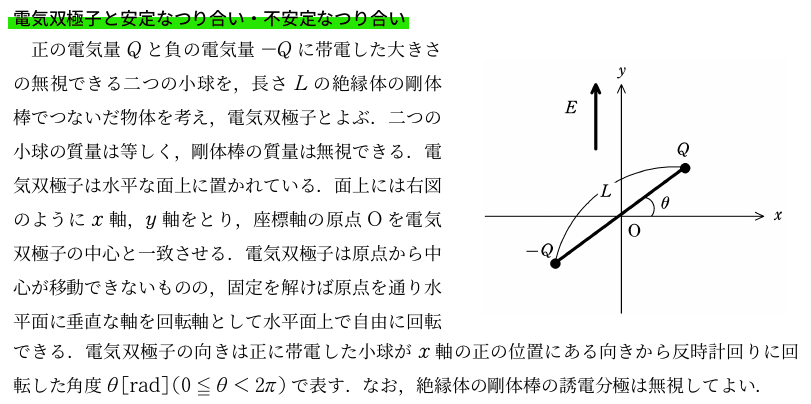
<問題>

<解答>
※ 以下,点電荷どうしが及ぼす静電気力がはたらきますが,棒と平行な力のため,力のモーメントに関係ないのでかいていません.
(1)
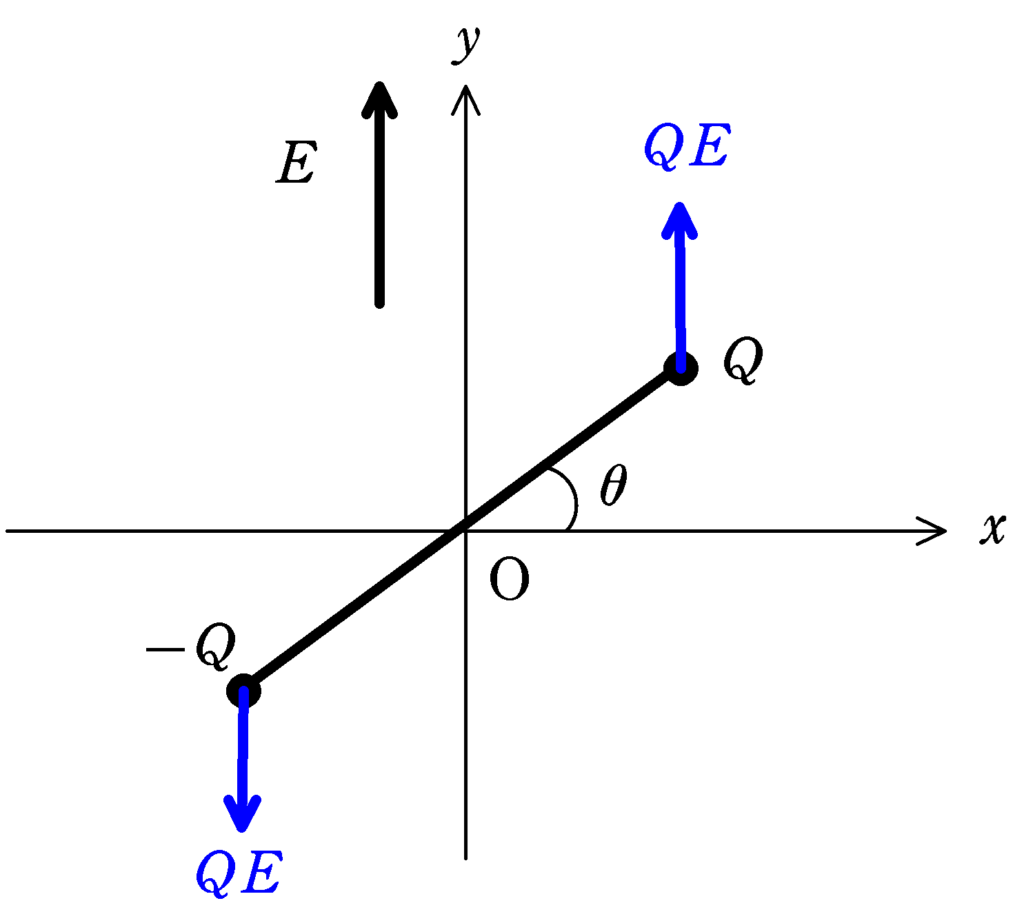
上図のとき,$Q$は電場と同じ方向に大きさ$QE$の力を受け,$-Q$は電場と反対方向に大きさ$QE$の力を受ける.
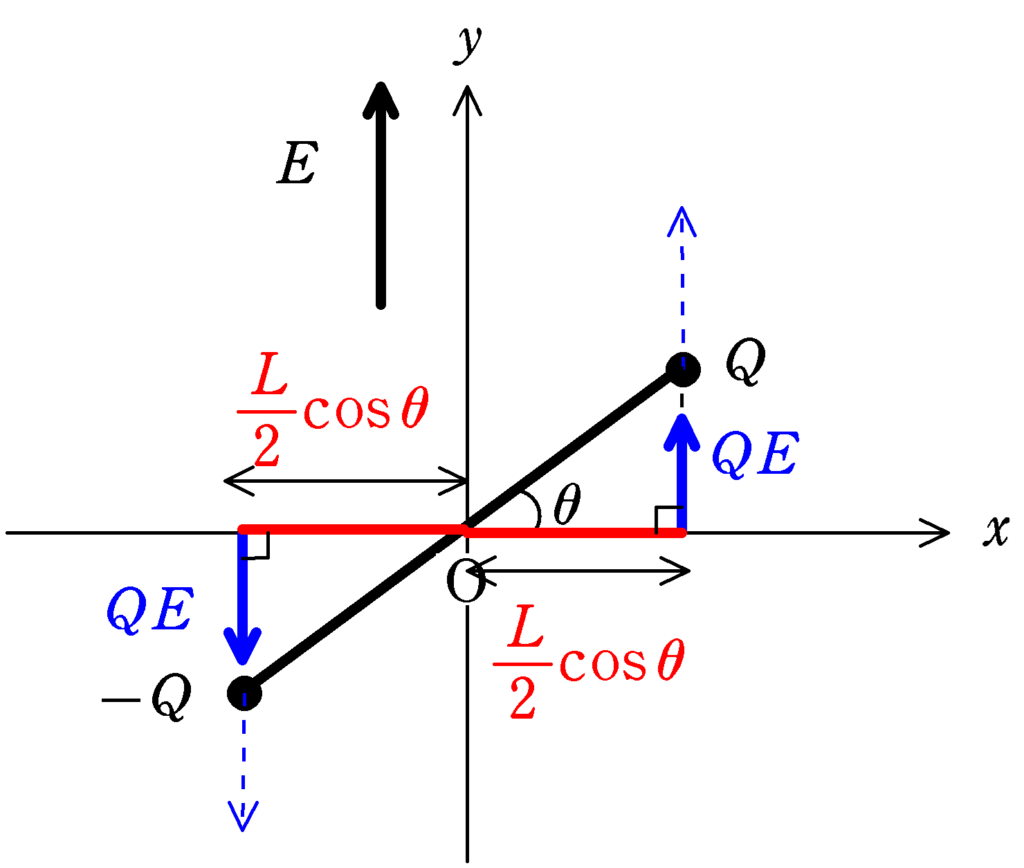
作用線平行移動の原理(詳しくはこちら)より,それぞれが受ける静電気力の力の作用点を$x$軸まで移動すると,Oからの距離は$\dfrac{L}{2}\cos\theta$であるから,$+Q$の電荷の受ける静電気力の力のモーメントは反時計回りに
$\dfrac{L}{2}\cos\theta\times QE$
中心を$\rm O$とし,ある始点にはたらく力のモーメントを計算するとき,力の作用線上のどこに移動させても力のモーメントは同じである.
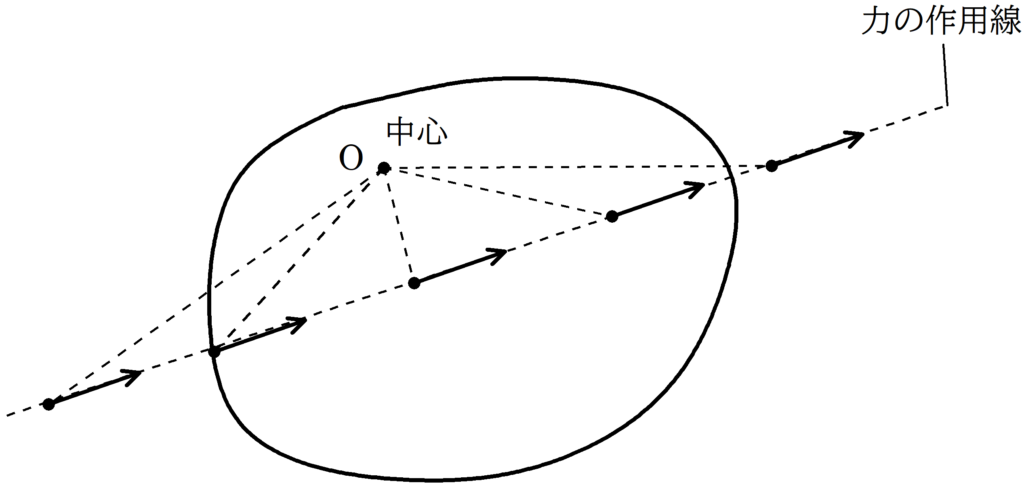
(説明の記事はこちら)
であり,同じく$-QE$も反時計回りに
$\dfrac{L}{2}\cos\theta\times QE$
なので,力のモーメントの和は
$\dfrac{L}{2}\cos\theta\times QE\times 2=QEL\cos\theta$ (答)
(2) 回転しないで静止しないには,力のモーメントの和が$0$であればよい.したがって
$\cos\theta=0$ $\therefore\,\, \theta=\dfrac{\pi}{2},\dfrac{3}{2}\pi$(答)
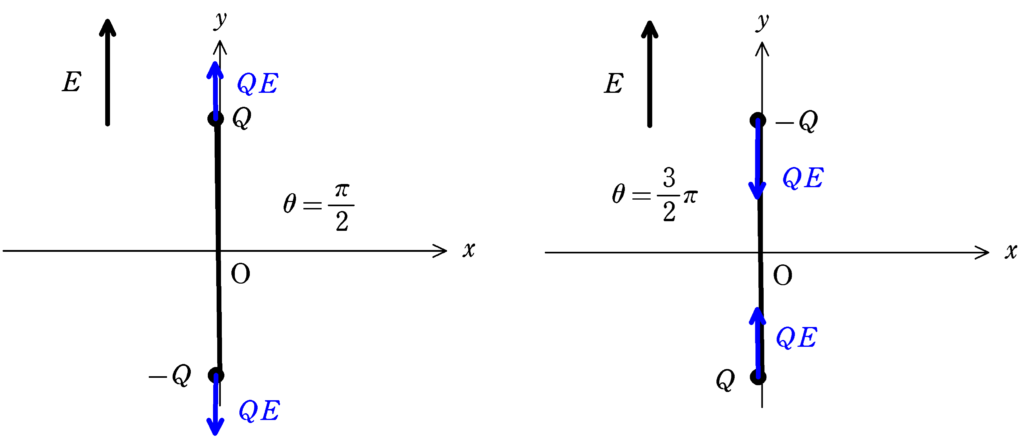
※ 確かに上図のような力であれば,回転しない.
(3) $\theta=\dfrac{\pi}{2},\dfrac{3}{2}\pi$から少しずらしたときにはたらく力を考えてみる.
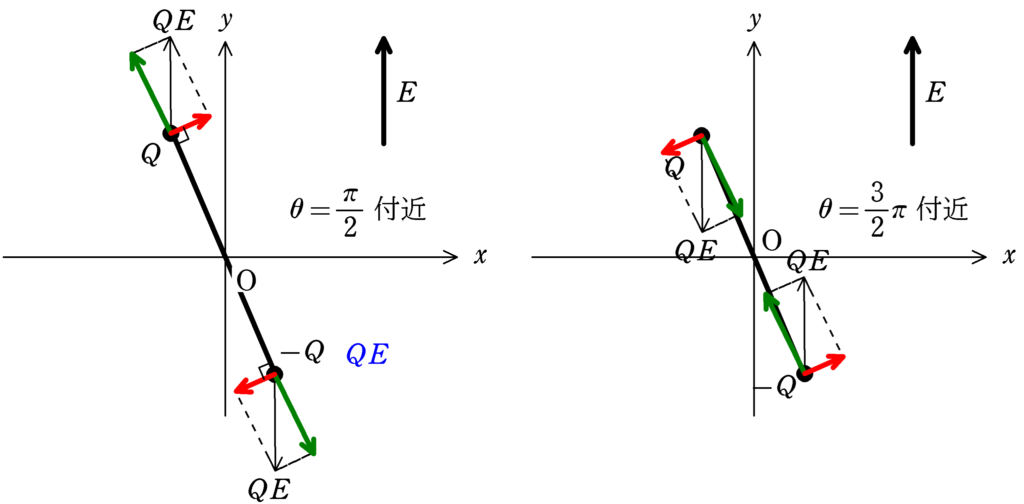
左上図のように$\theta=\dfrac{\pi}{2}$のとき,静電気力を剛体棒の方向(緑色の矢印)と,それに垂直な方向(赤色の矢印)に分解する.剛体棒の方向はつりあっているのでよい.垂直な方向,つまり赤矢印の力の成分が$\theta=\dfrac{\pi}{2}$にもどるようにはたらいている.上図は$\theta=\dfrac{\pi}{2}$より少し大きな角度のときをかいたが,$\theta=\dfrac{\pi}{2}$より少し小さな角度になったときも,やはり$\theta=\dfrac{\pi}{2}$に戻るように力がはたらき,赤い矢印の力が復元力となり振動運動をする.
一方,$\theta=\dfrac{3}{2}\pi$付近(右上図)では,逆に$\theta=\dfrac{2}{3}\pi$から離れるように力がはたらいてしまうので不適.
以上から,適するのは$\theta=\dfrac{\pi}{2}$(答)
ちなみに,$\theta=\dfrac{\pi}{2}$のように,つり合いの位置から少しずらしたときに元の場所にもどってくるようなものを「安定なつり合い」という.逆に,つり合いの位置から少しずらしたときに元の場所から離れていってしまうようなものを「不安定なつり合い」という.
下図のように,剛体棒に物体がとりつけられ,重力下にあるときを考えてみる.
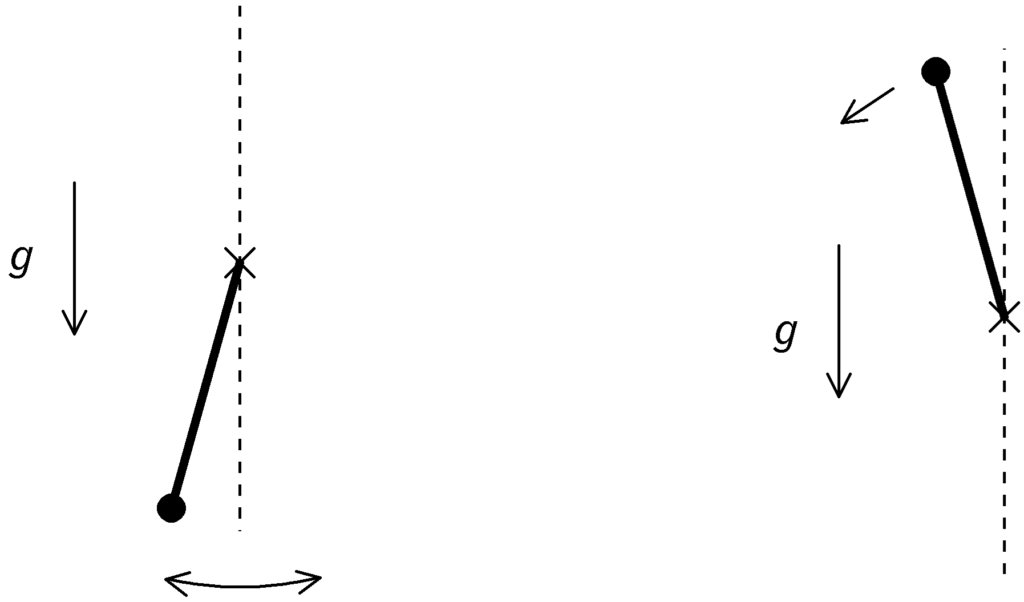
左上図のように,固定点から真下の位置にあるときが「安定なつり合い」(少しずらすともとにもどるようにする),逆に上にあるとき(右上図)が「不安定なつり合い」である.



コメント