
今回はよくある熱効率の計算の間違いについて話をします.
間違い例も含めて紹介します.
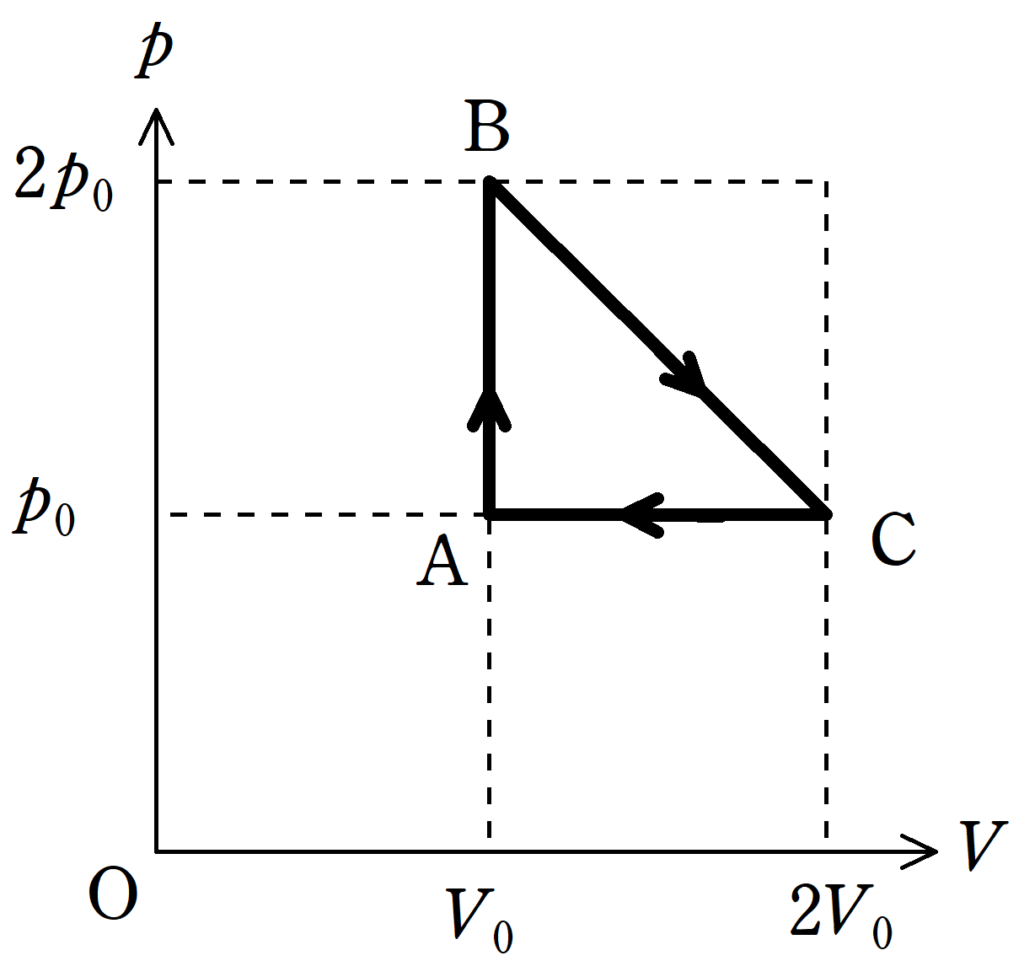
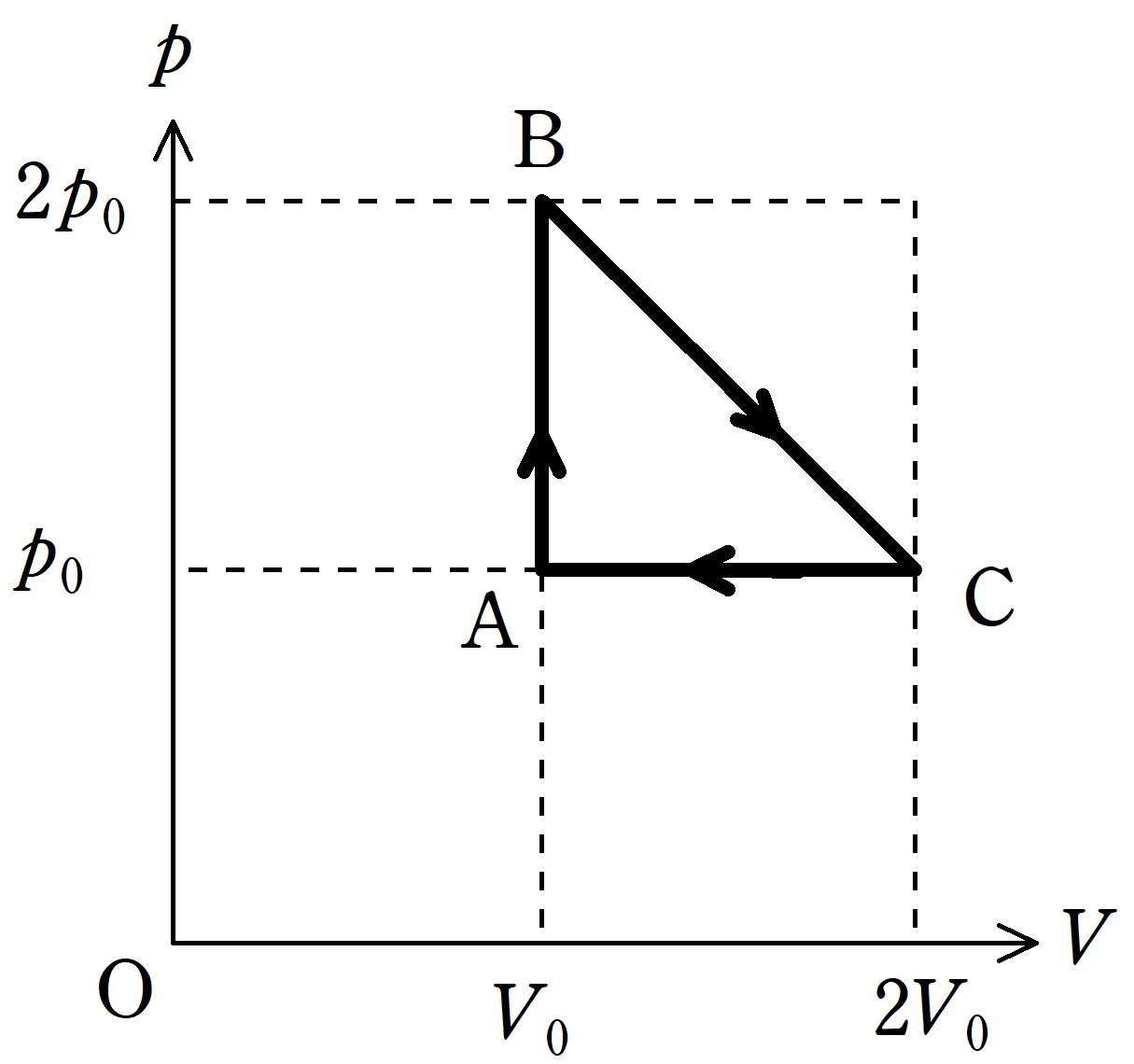
上図は縦軸が気体の圧力$p$,横軸が気体の体積$V$のグラフである.気体は単原子分子理想気体で,A→B→C→Aの順に準静的変化をする.A→B→C→Aの1サイクルにおける熱効率$e$を求めよ.

熱効率の定義は次のようになります.
吸収した熱量を$Q_{\rm{in}}$,放出した熱量を$Q_{\rm_{out}}$,気体が正味のした仕事(気体がした正の仕事,負の仕事を符号付きですべて足すこと)を$W_{気体}$とすると,熱効率$e$は
$e=\dfrac{W_{気体}}{Q_{\rm{in}}}=\dfrac{Q_{\rm{in}}-Q_{\rm{out}}}{Q_{\rm{in}}}=1-\dfrac{Q_{\rm{out}}}{Q_{\rm{in}}}$
<間違い例>
A→B→C→Aの間に気体がした仕事$W$は,$\bigtriangleup{\rm ABC}$の面積を求めて
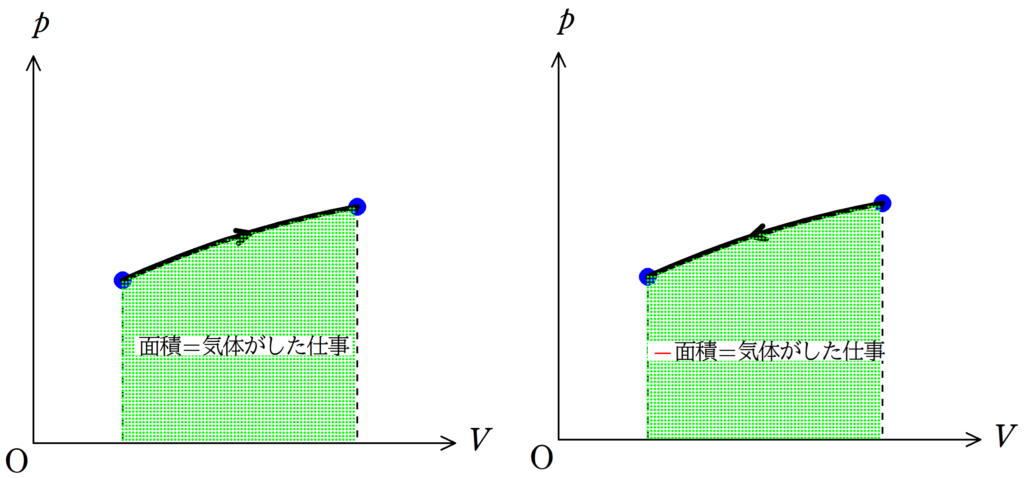
気体がした仕事は上図のように緑色部分の面積を求めることで計算ができる.
ただし,状態変化の矢印が右向きのときは
面積=気体がした仕事
であるが,状態変化の矢印が左向きのときは
-面積=気体がした仕事
である.
$W=\dfrac{1}{2}(2V_{0}-V_{0})\cdot (2p_{0}-p_{0})=\dfrac{1}{2}p_{0}V_{0}$ $\dots (\ast)$
★ AB間に吸収する熱量$Q_{\rm AB}$
定積変化なので,気体がした仕事0.
問題分に単原子分子理想気体とかいてあるときは,次のことを使うことができる.
定積モル比熱が$\dfrac{3}{2}R$である.すなわち
内部エネルギー$U$は
$U=\dfrac{3}{2}nRT=\dfrac{3}{2}pV$
内部エネルギーの変化$\Delta U$は
$\Delta U=\dfrac{3}{2}nR\Delta T=\dfrac{3}{2}(p_{2}V_{2}-p_{1}V{1})$
※$n$:物質量,$T$:絶対温度,$p$:圧力,$V$:体積
内部エネルギー変化は$\dfrac{3}{2}(2p_{0}V_{0}-p_{0}V_{0})=\dfrac{3}{2}p_{0}V_{0}$なので,熱力学第一法則より
内部エネルギーの変化を$\Delta U$,気体が吸収する熱量を$Q$,気体がした仕事を$W$とすると
$Q=\Delta U+W$
AB間に吸収する熱量$Q_{\rm AB}$は
$Q_{\rm AB}=\dfrac{3}{2}p_{0}V_{0}$ $\dots (2\ast)$
★ BC間に吸収した熱量$Q_{\rm BC}$
BC間に気体がした仕事$W_{\rm BC}$は,下図の青色部分の面積を求めて
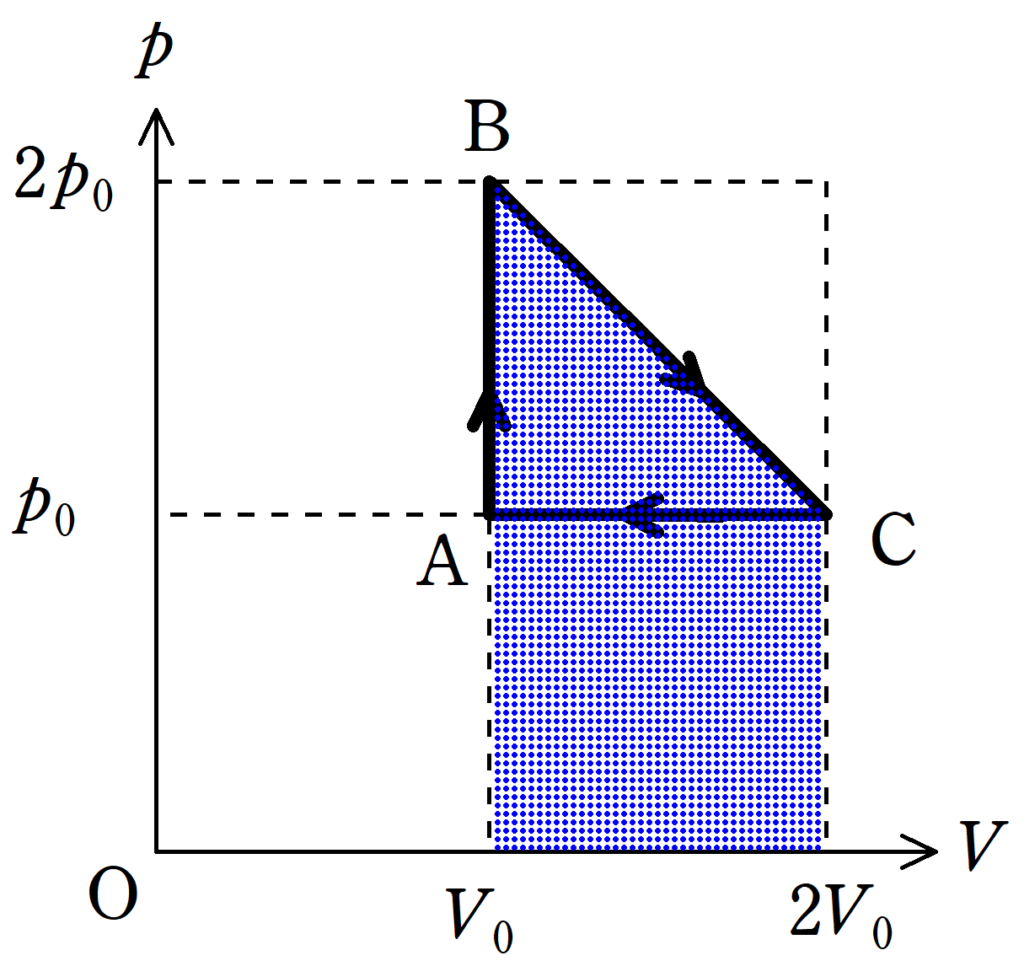
$W_{\rm BC}=\dfrac{1}{2}(p_{0}+2p_{0})\cdot (2V_{0}-V_{0})=\dfrac{3}{2}p_{0}V_{0}$
内部エネルギー変化$\varDelta U_{\rm BC}$は
$\varDelta U_{\rm BC}=\dfrac{3}{2}(p_{0}\cdot 2V_{0}-2p_{0}\cdot V_{0})=0$
したがって,熱力学第一法則より,BC間で吸収した熱量$Q_{\rm BC}$は
$Q_{\rm BC}=0+\dfrac{3}{2}p_{0}V_{0}=\dfrac{3}{2}p_{0}V_{0}$ $\dots (3\ast)$
★ CA間に放出する熱量$Q_{\rm CA}$
CA間に気体がした仕事$W_{\rm CA}$は
$W_{\rm CA}=-p_{0}V_{0}$
内部エネルギー変化$\varDelta U_{\rm CA}$は
$\varDelta U_{\rm CA}=\dfrac{3}{2}(p_{0}V_{0}-p_{0}\cdot 2V_{0})=-\dfrac{3}{2}p_{0}V_{0}$
熱力学第一法則より
$-Q_{\rm CA}=-p_{0}V_{0}-\dfrac{3}{2}p_{0}V_{0}=-\dfrac{5}{2}p_{0}V_{0}$
$\therefore Q_{\rm CA}=\dfrac{5}{2}p_{0}V_{0}$ $\dots (4\ast)$
$(2\ast)$,$(3\ast)$より,熱効率$e$は
$\eqalign{e&=\dfrac{W}{Q_{\rm AB}+Q_{\rm BC}}\\&=\dfrac{\dfrac{1}{2}\cancel{p_{0}V_{0}}}{\dfrac{3}{2}\cancel{p_{0}V_{0}}+\dfrac{3}{2}\cancel{p_{0}V_{0}}}\\&=\dfrac{1}{6}}$ (間違った答え)

これはなんで間違いなの?

実は,B→Cの途中で,気体は吸収から放熱に切り替わっているんです.
こちらでも扱っています.

では,どこで切り替わるのか計算していきましょう.
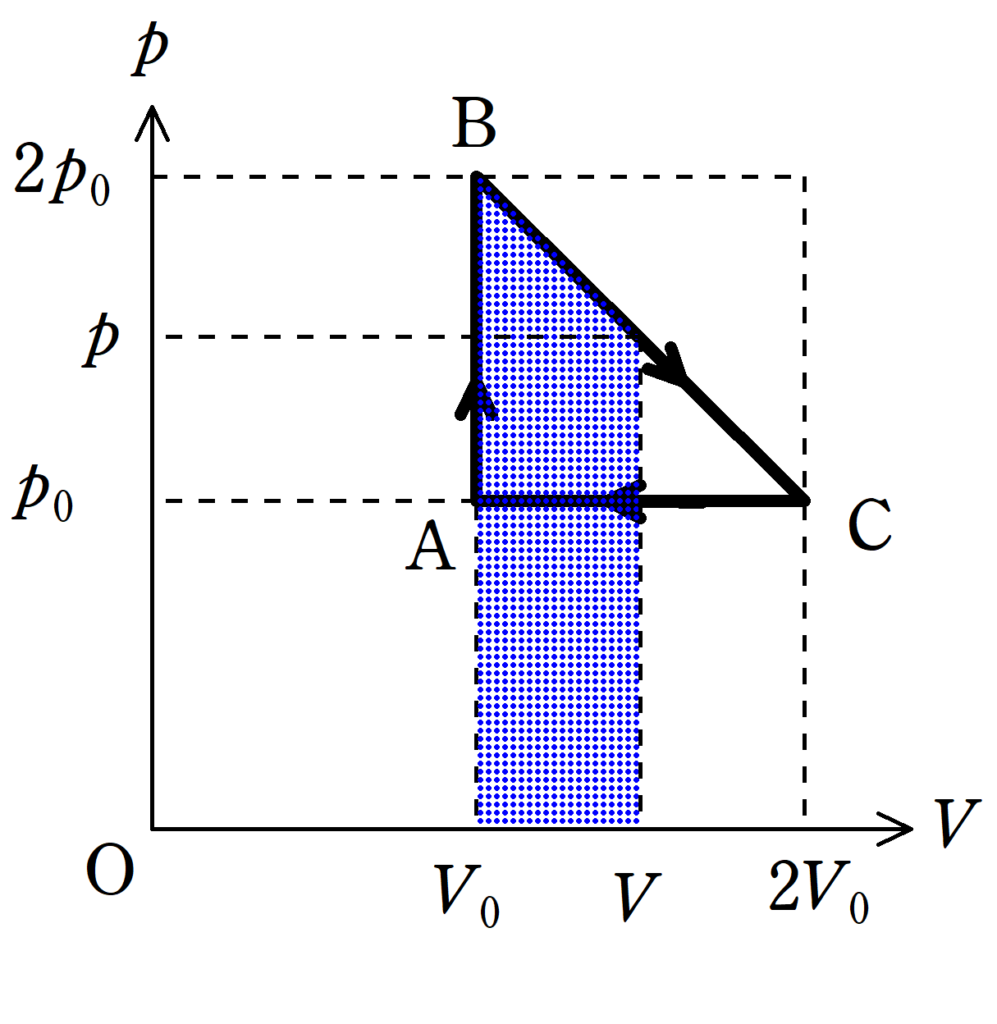

直線BCの式は
$p-2p_{0}=\dfrac{p_{0}-2p_{0}}{2V_{0}-V_{0}}(V-V_{0})$
$\therefore$ $p=-\dfrac{p_{0}}{V_{0}}V+3p_{0}$
となります.
また,Bから体積が$V$になるまでに気体がした仕事$W$は
$W=\dfrac{1}{2}(p+2p_{0})(V-V_{0})$ $\dots (5\ast)$
$(5\ast)$に$p=-\dfrac{p_{0}}{V_{0}}V+3p_{0}$を代入して
$\eqalign{W&=\dfrac{1}{2}\left(-\dfrac{p_{0}}{V_{0}}V+3p_{0}+2p_{0}\right)(V-V_{0})\\&=-\dfrac{1}{2}\left(\dfrac{p_{0}}{V_{0}}V-5p_{0}\right)(V-V_{0})\\&=-\dfrac{p_{0}}{2V_{0}}V^{2}+3p_{0}V-\dfrac{5}{2}p_{0}V_{0} \dots (6\ast)}$
また,内部エネルギー変化$\varDelta U$は
$\eqalign{\Delta U&=\dfrac{3}{2}(pV-2p_{0}\cdot V_{0})\\&=\dfrac{3}{2}\left\{\left(-\dfrac{p_{0}}{V_{0}}V+3p_{0}\right)V-2p_{0}V_{0}\right\}\\&=-\dfrac{3p_{0}}{2V_{0}}V^{2}+\dfrac{9}{2}p_{0}V-3p_{0}V_{0}
\dots (7\ast)}$
$(6\ast)$,$(7\ast)$から熱力学第一法則より
$\eqalign{Q&=\Delta U+W\\&=-\dfrac{3p_{0}}{2V_{0}}V^{2}+\dfrac{9}{2}p_{0}V-3p_{0}V_{0}+-\dfrac{p_{0}}{2V_{0}}V^{2}+3p_{0}V-\dfrac{5}{2}p_{0}V_{0}\\&=-\dfrac{2p_{0}}{V_{0}}V^{2}+\dfrac{15}{2}p_{0}V-\dfrac{11}{2}p_{0}V_{0}}$

$Q$は平方完成して次のように変形でいます.
$Q=-\dfrac{2p_{0}}{V_{0}}\left(V-\dfrac{15}{8}V_{0}\right)^{2}+\dfrac{49}{32}p_{0}V_{0}$
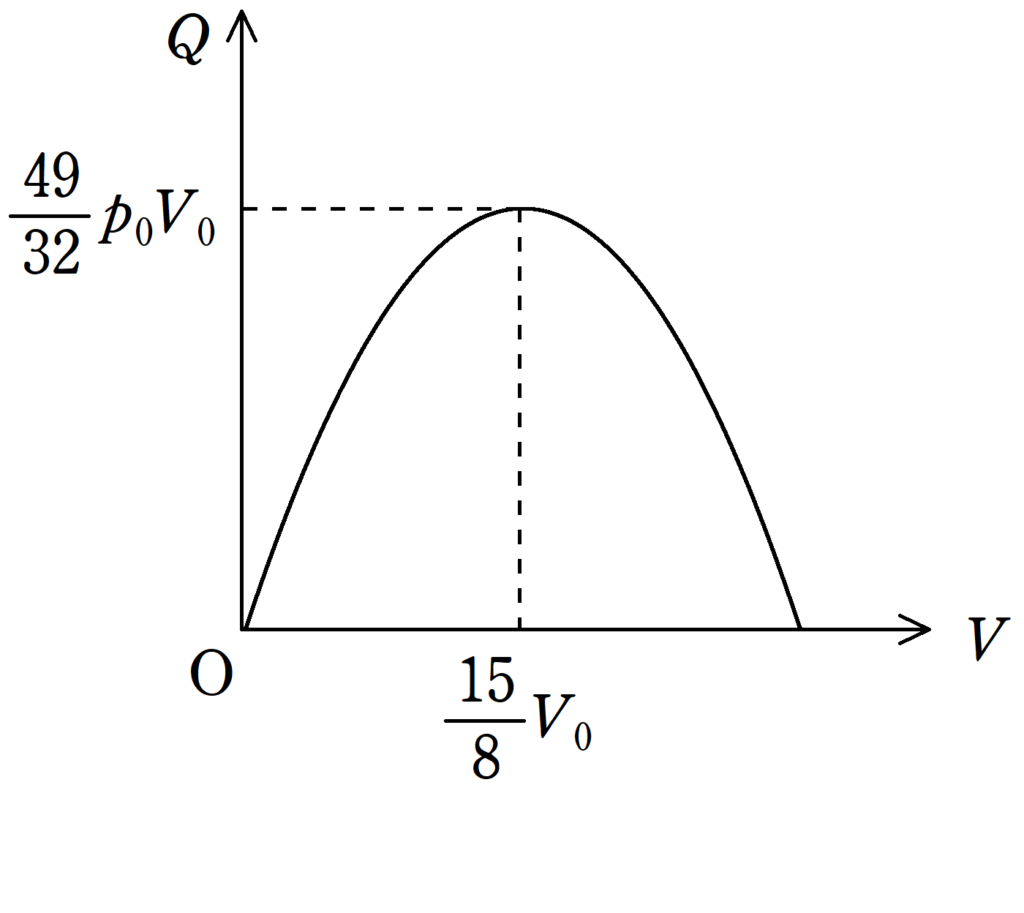

縦軸を$Q$,横軸を$V$としたグラフをかくと上のようになります.
上のグラフによれば,$V=\dfrac{15}{8}V_{0}$になるまでは$Q$が増えています.つまり,熱量を吸収しています.
一方,$V=\dfrac{15}{8}V_{0}$を超えると,$Q$が減っています.つまり,熱量を放出しています.
熱効率を計算する際は分母は吸収した熱量のみを代入する必要があります.今回代入するのは,$(3\ast)$で求めた$\dfrac{3}{2}p_{0}V_{0}$ではなく,$\dfrac{49}{32}p_{0}V_{0}$です.
したがって,正しい熱効率は
$e=\dfrac{W}{Q_{\rm AB}+\dfrac{49}{32}p_{0}V_{0}}=\dfrac{\dfrac{1}{2}p_{0}V_{0}}{\dfrac{3}{2}p_{0}V_{0}+\dfrac{49}{32}p_{0}V_{0}}=\dfrac{16}{97}$ (答)

このように,傾きが負の直線の熱効率の計算は注意が必要です.

コメント