$pV$グラフの読み取り演習5 右下がりの直線グラフ

PHYさん

今回は，右下がりの直線のグラフです．

このグラフでは，熱量の正負が入れ替わることがあるため

注意が必要です．

問題

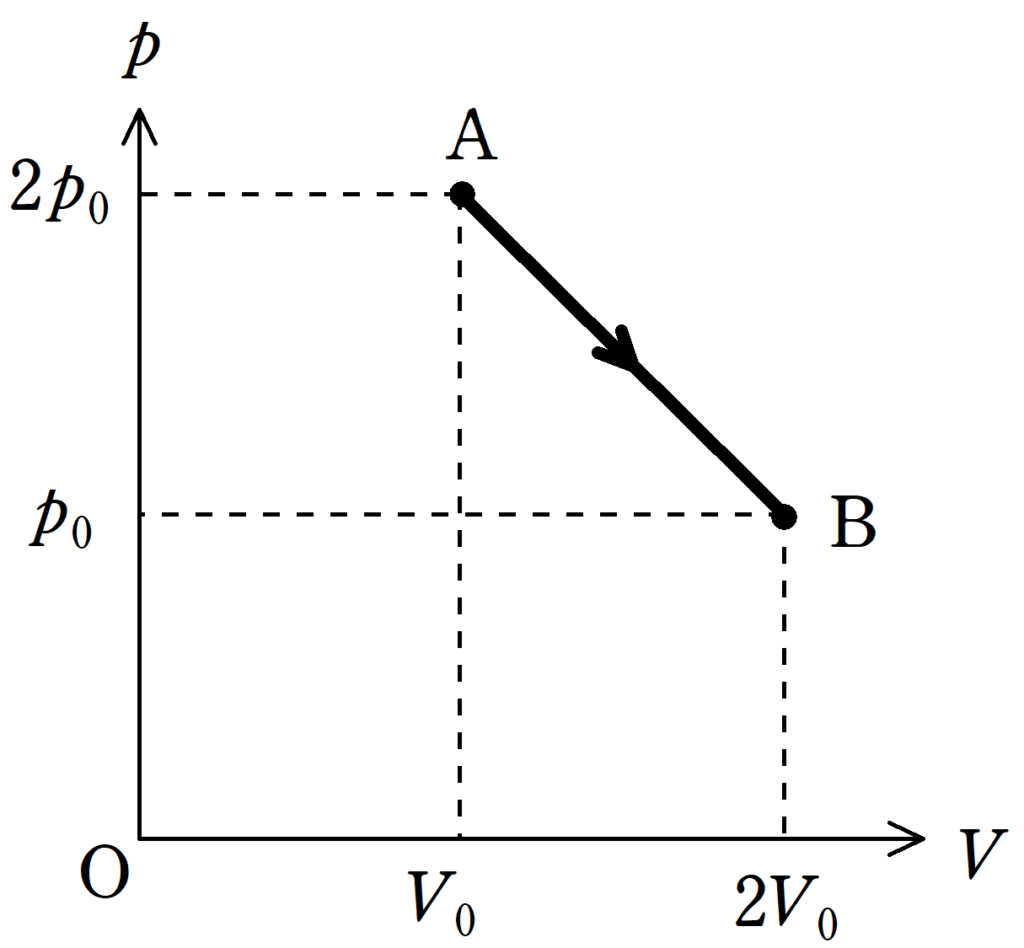
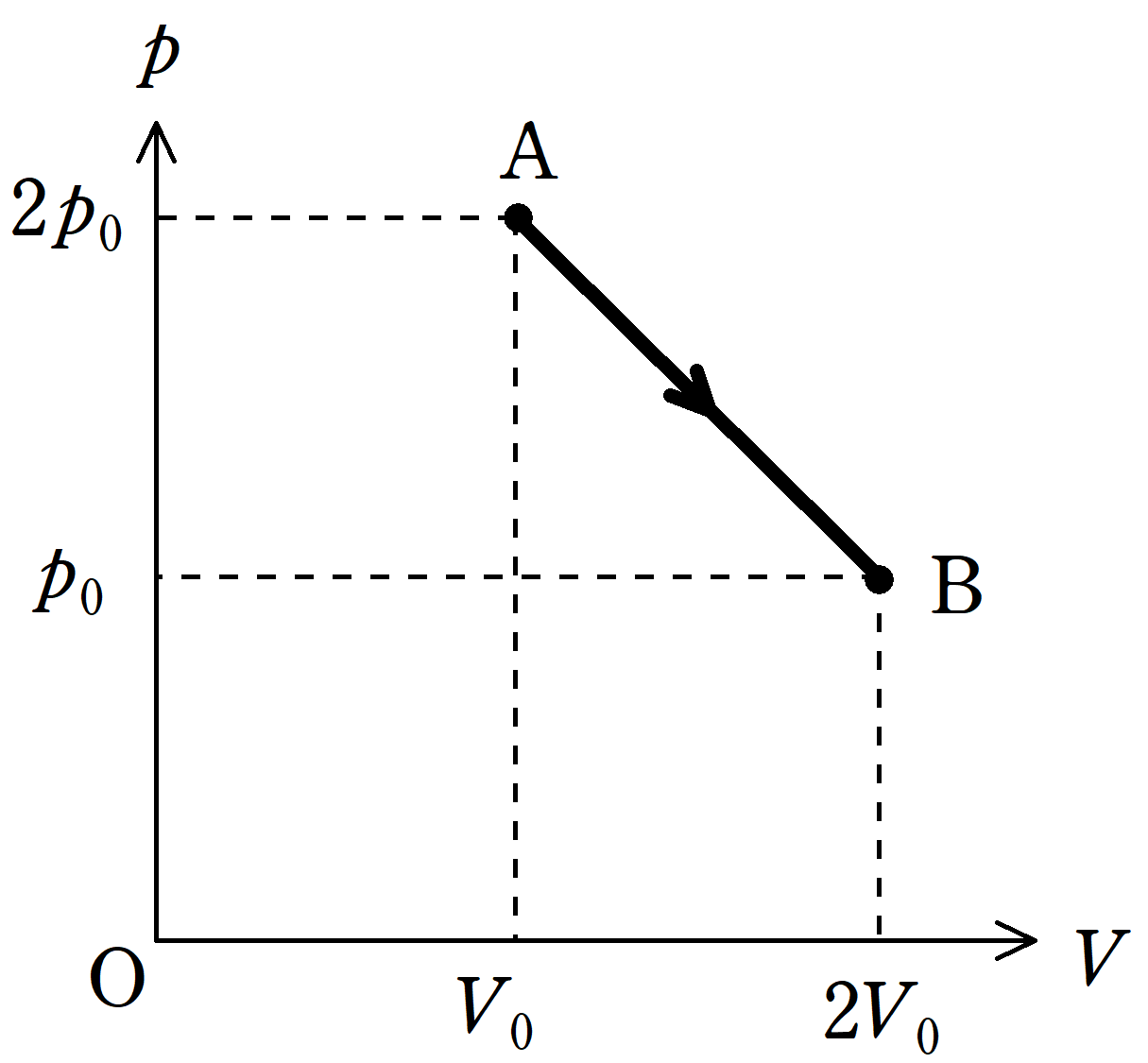
上のような$pV$図を考える．状態Aでの圧力は$2p_{0}$，体積は$V_{0}$，絶対温度は$T_{0}$である．

状態Aから直線的に，圧力$p_{0}$，体積$2V_{0}$の状態Bに変化させる．

気体は単原子分子理想気体として，次の問いに答えよ．

(1)　状態Bの絶対温度$T_{\rm B}$を求めよ．

(2)　状態Aから状態Bに変化させる途中の体積$V$$(V_{0}\leqq V\leqq 2V_{0})$の状態Pを考える．状態Aから状態Pまでに気体がした仕事$W$を$V , p_{0} , V_{0}$を用いて表せ．

(3)　状態Aから状態Pまでの間の内部エネルギーの変化$\Delta U$を$V , p_{0} , V_{0}$を用いて表せ．

(4)　状態Aから状態Pまでの熱量$Q$を求めよ．また，体積を増やしたときの熱量$Q$が増加から減少に転じるときの体積を求めよ．

<解答>

(1)

NEKO

$T_{\rm B}$は次のことを使いましょう！

$pV$図の読みとり①　絶対温度

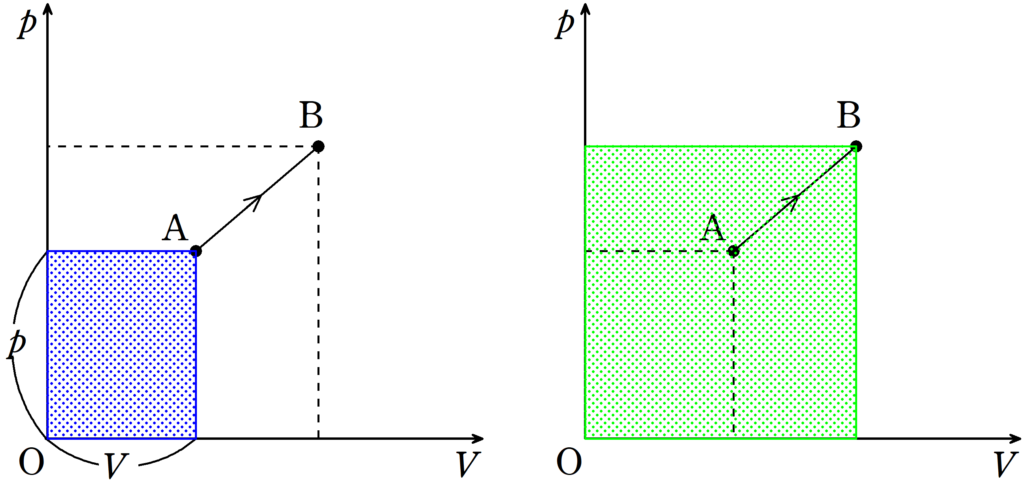
絶対温度は状態の点から$p$軸$V$軸へ下した垂線の足と原点でつくられる長方形の面積に比例する．

NEKO

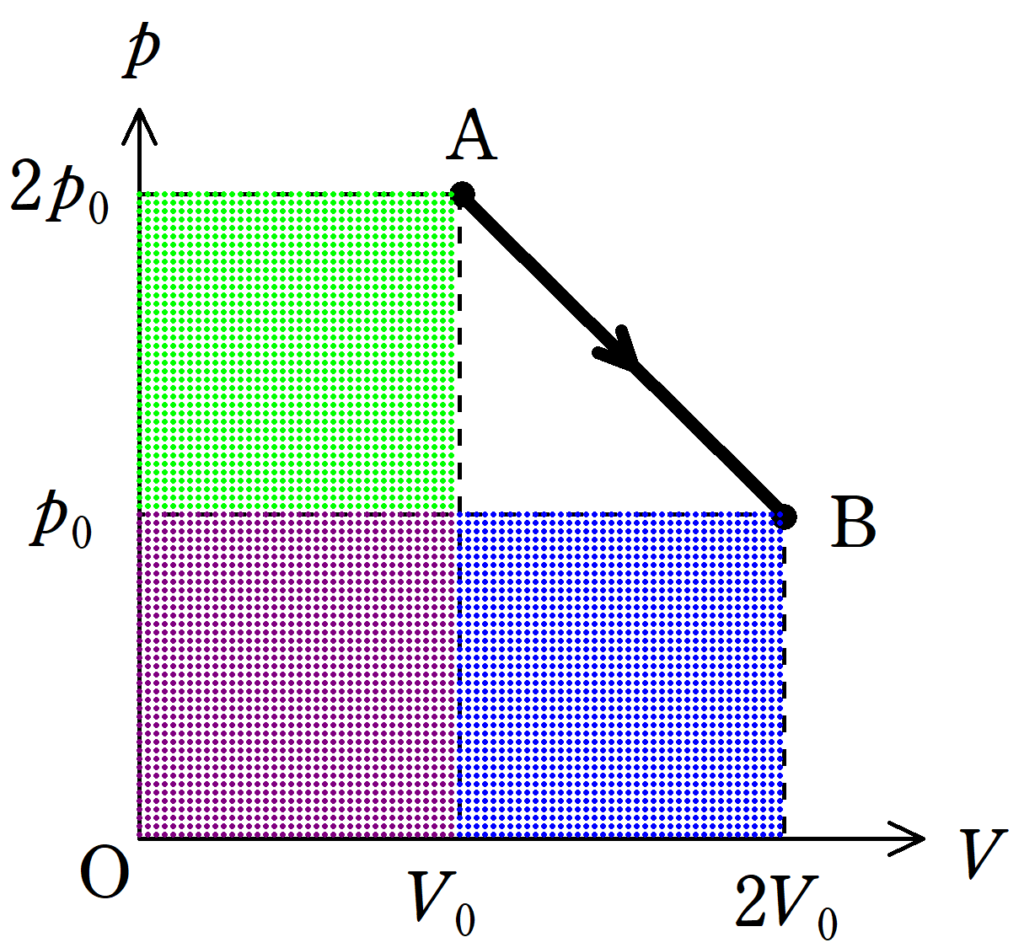
AとOでつくられる長方形の面積は$2p_{0}V_{0}$で，BとOでつくられる長方形の面積も$2p_{0}V_{0}$だから，AとBの絶対温度は同じだね．

答え：$T_{\rm B}=T_{0}$

(2)

PHYさん

気体がした仕事は，次のことを用います．

$pV$図の読み取り②　気体がした仕事

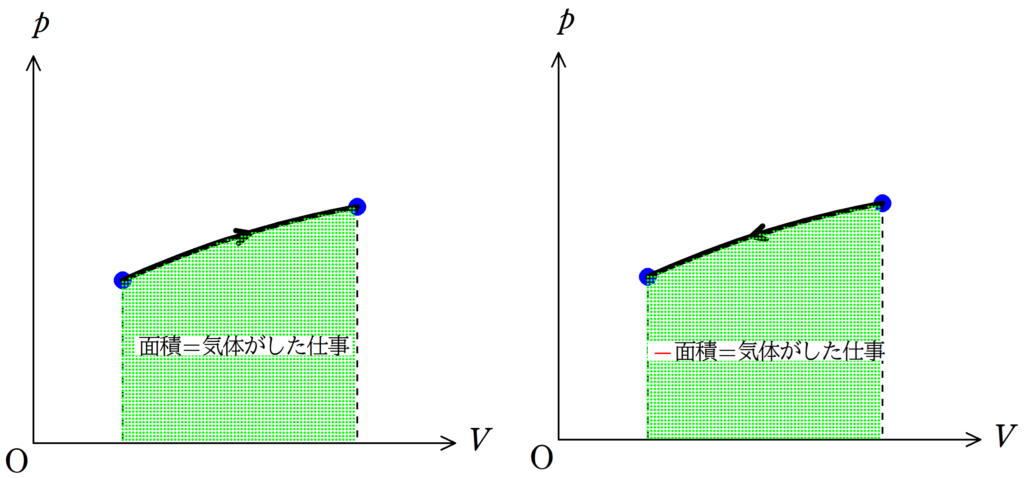
気体がした仕事は上図のように緑色部分の面積を求めることで計算ができる．

ただし，状態変化の矢印が右向きのときは

面積＝気体がした仕事

であるが，状態変化の矢印が左向きのときは

-面積＝気体がした仕事

である．

NEKO

今回は下図の赤色部分の台形の面積を求めればいいね．

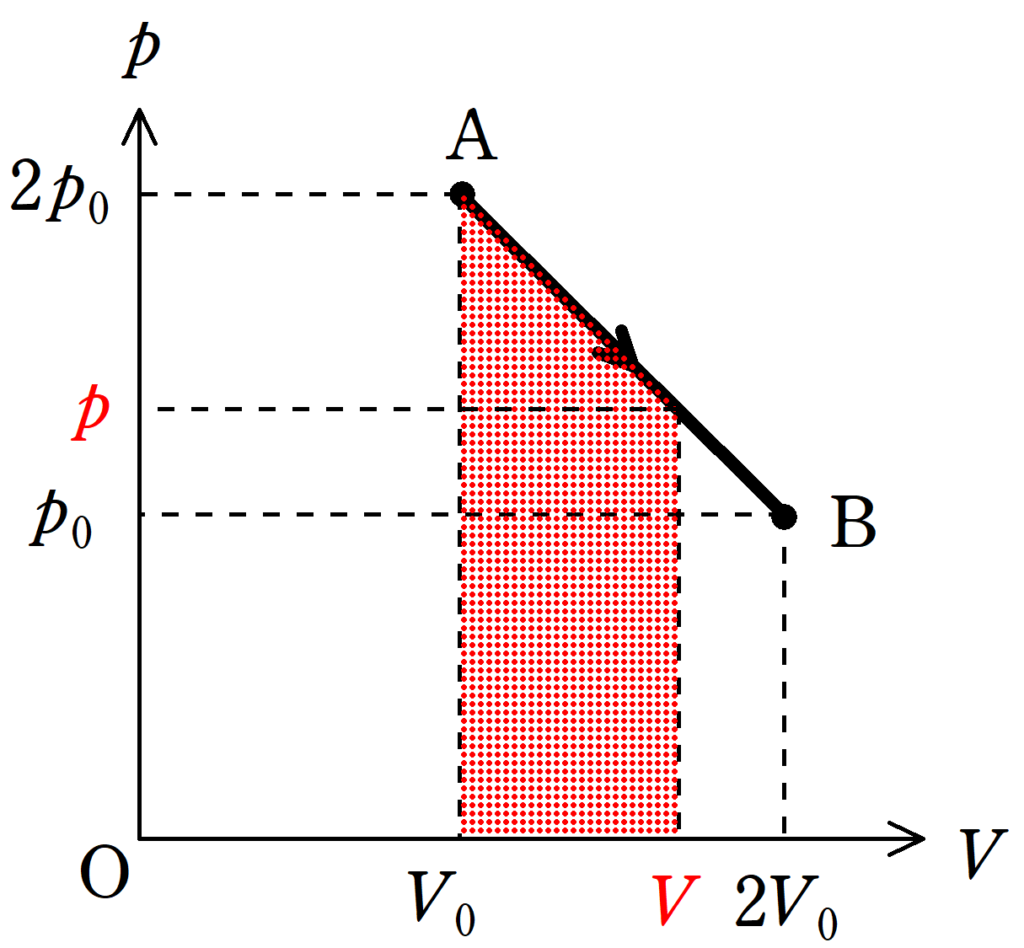
$W=\dfrac{1}{2}(p+2p_{0})(V-V_{0})$　$\dots　(\ast)$

2点を通る直線の式

$xy$平面上の2点$(x_{1} , y_{1})$と$(x_{2} , y_{2})$を通る直線の式は$x_{1}\neq x_{2}$のとき，次のようになる．

$y-y_{1}=\dfrac{y_{2}-y_{1}}{x_{2}-x_{1}}(x-x_{1})$

NEKO

なので，直線ABの式は

$p-2p_{0}=\dfrac{p_{0}-2p_{0}}{2V_{0}-V_{0}}(V-V_{0})$

$\therefore$　$p=-\dfrac{p_{0}}{V_{0}}V+3p_{0}$

となります．

したがって，$(\ast)$に代入すると

$\eqalign{W&=\dfrac{1}{2}(-\dfrac{p_{0}}{V_{0}}V+3p_{0}+2p_{0})(V-V_{0})\\&=-\dfrac{1}{2}(\dfrac{p_{0}}{V_{0}}V-5p_{0})(V-V_{0})\\&=-\dfrac{p_{0}}{2V_{0}}V^{2}+3p_{0}V-\dfrac{5}{2}p_{0}V_{0}}$　(答)

(3)　

PHYさん

内部エネルギーの変化は次の式を使います．

単原子分子理想気体の内部エネルギー

問題文に単原子分子理想気体とかいてあるときは，次のことを使うことができる．

定積モル比熱が$\dfrac{3}{2}R$である．すなわち

内部エネルギー$U$は

$U=\dfrac{3}{2}nRT=\dfrac{3}{2}pV$

内部エネルギーの変化$\Delta U$は

$\Delta U=\dfrac{3}{2}nR\Delta T=\dfrac{3}{2}(p_{2}V_{2}-p_{1}V{1})$

※$n$：物質量，$T$：絶対温度，$p$：圧力，$V$：体積

$\eqalign{\Delta U&=\dfrac{3}{2}(pV-2p_{0}\cdot V_{0})\\&=\dfrac{3}{2}\{(-\dfrac{p_{0}}{V_{0}}V+3p_{0})V-2p_{0}V_{0}\}\\&=-\dfrac{3p_{0}}{2V_{0}}V^{2}+\dfrac{9}{2}p_{0}V-3p_{0}V_{0}
}$　(答)

(4)

PHYさん

熱量は，熱力学第一法則を立てましょう．

熱力学第一法則

内部エネルギーの変化を$\Delta U$，気体が吸収する熱量を$Q$，気体がした仕事を$W$とすると

$Q=\Delta U+W$

熱力学第一法則より

$\eqalign{Q&=\Delta U+W\\&=-\dfrac{3p_{0}}{2V_{0}}V^{2}+\dfrac{9}{2}p_{0}V-3p_{0}V_{0}+-\dfrac{p_{0}}{2V_{0}}V^{2}+3p_{0}V-\dfrac{5}{2}p_{0}V_{0}\\&=-\dfrac{2p_{0}}{V_{0}}V^{2}+\dfrac{15}{2}p_{0}V-\dfrac{11}{2}p_{0}V_{0}}$ (答)

NEKO

$V$が変化したとき$Q$の変化をきかれているので，$\dfrac{dQ}{dV}$を調べましょう．

$\dfrac{dQ}{dV}=-\dfrac{4p_{0}}{V_{0}}V+\dfrac{15}{2}p_{0}$

$\dfrac{dQ}{dV}=0$となるときの$V$は

$\therefore$　$V=\dfrac{15}{8}V_{0}$