
前回の内容はこちらです.
引き続き,位相差の演習問題を解いていきましょう.
前回の問題とかなり似ていますが,今回の問題では,$\rm S_{1}$と$\rm S_{2}$は逆位相になっています.
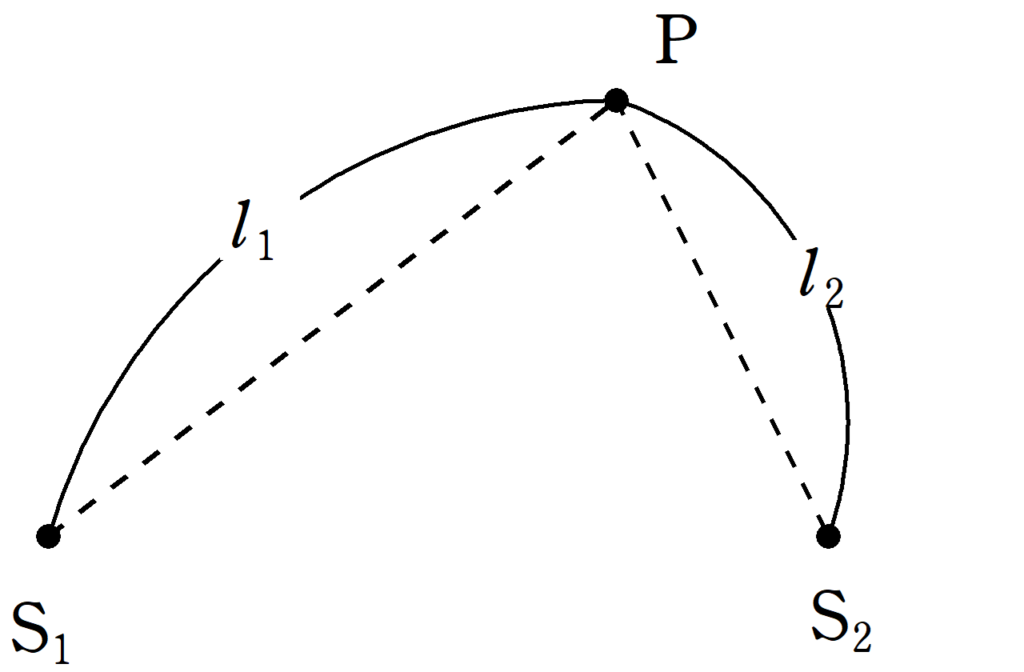
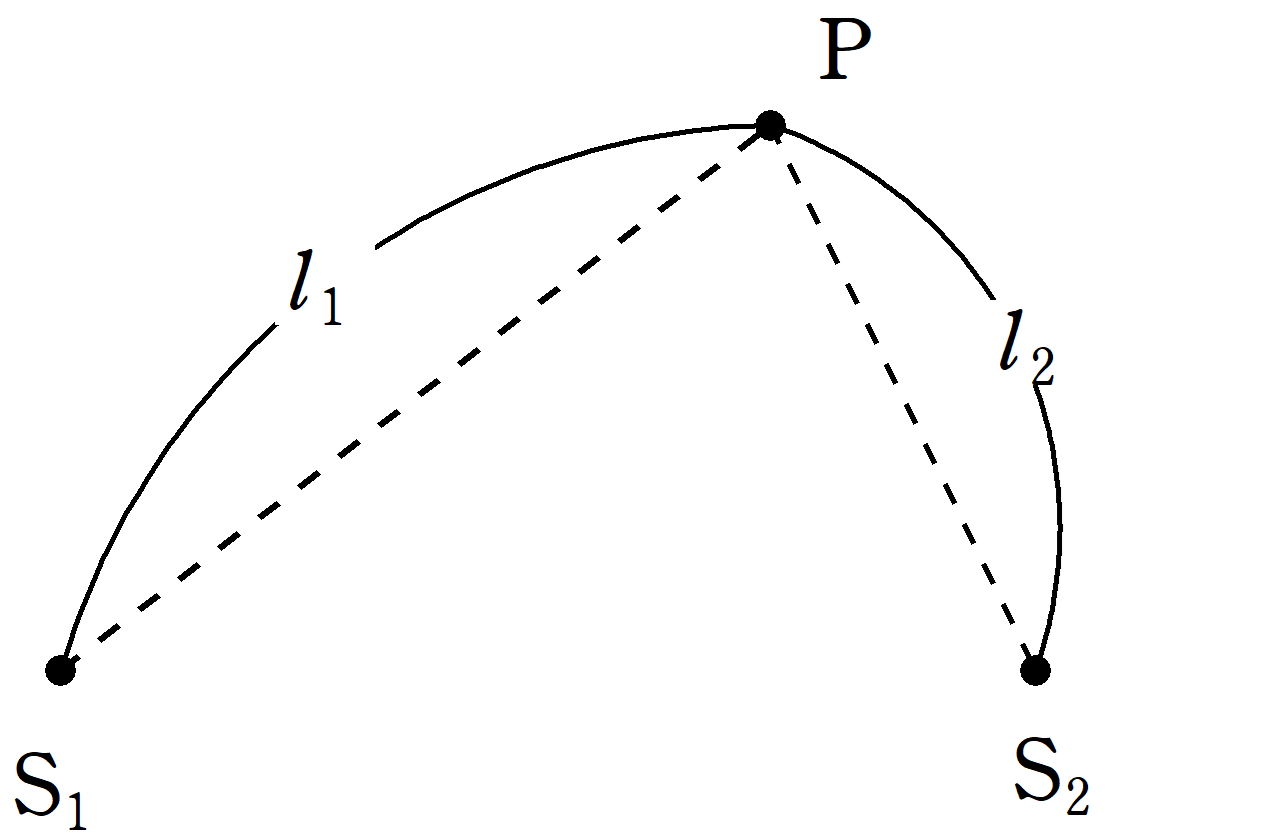
波源$\rm S_{1}$,$\rm S_{2}$があり,波源$\rm S_{1}$では時刻$t$において,$y_{1}=A\sin\left(2\pi ft\right)$で振動していて,波源$\rm S_{2}$では,$y_{2}=A\sin\left(2\pi ft+\pi\right)$で振動している.ただし,$A$は振幅,$f$は振動数であり,どちらも正の定数である.${\rm S_{1}P}=l_{1}$,${\rm S_{2}P}=l_{2}$であるような点$\rm P$がある.このとき,次の問いに答えよ.ただし,伝わる波の波長を$\lambda$とする.
(1) $\rm S_{1}$から$\rm P$に伝わる波の$\rm P$における媒質の変位と$\rm S_{2}$から$\rm P$に伝わる波の$\rm P$における媒質の変位の位相差$\varDelta \varphi$を$\lambda$,$l_{1}$,$l_{2}$を用いて表せ.
(2) 2つの波が強め合うときの条件を整数$k$および,$l_{1}$,$l_{2}$,$\lambda$を用いてかけ.
(3) 2つの波が弱め合うときの条件を整数$k$および,$l_{1}$,$l_{2}$,$\lambda$を用いてかけ.
(1)

波が伝わる速さを$V$とすると,$\rm S_{1}$から$\rm P$に伝わる波において,$\rm P$で媒質の変位は,時間$\dfrac{l_{1}}{V}$前の$\rm S_{1}$での振動と等しいんだよね.
したがって,媒質の変位$y_{1\rm P}$は
$y_{1\rm P}=A\sin\left\{2\pi f\left(t-\dfrac{l_{1}}{V}\right) \right\}$

このとき,位相$\varphi_{1}$は,波の基本式,$V=f\lambda$も用いると次のようになります.
$\varphi_{1}=2\pi f\left(t-\dfrac{l_{1}}{V}\right)=2\pi ft-\dfrac{2\pi }{\lambda}l_{1}$

同じように,$\rm S_{2}$から$\rm P$に伝わる波の$\rm P$における媒質の位相$\varphi_{2}$は
$\varphi_{2}=2\pi f\left(t-\dfrac{l_{2}}{V}\right)+\pi=2\pi ft-\dfrac{2\pi }{\lambda}l_{2}+\pi$

したがって,位相差$\varDelta \varphi$は
$\varDelta \varphi=\varphi_{1}-\varphi_{2}=\dfrac{2\pi}{\lambda}(l_{2}-l_{1})-\pi$ (答)
(2)

強め合うのは,$\varDelta \varphi$が$2\pi$の整数倍になるときなので
$\varDelta \varphi=2\pi k$
$\therefore \dfrac{2\pi}{\lambda}(l_{2}-l_{1})-\pi=2\pi k$

さらに変形すると,
$l_{2}-l_{1}=\left(k+\dfrac{1}{2}\right)\lambda$
のように,よく見る普通(?)の強め合いの条件とは逆の形が出てくるね.
(3)

弱め合うのは,$\varDelta \varphi$が$\pi$の奇数倍のときなので
$\varDelta \varphi=(2k-1)\pi$
$\therefore \dfrac{2\pi}{\lambda}(l_{2}-l_{1})-\pi=(2k-1)\pi $(答)

同様に,
$l_{2}-l_{1}=k\lambda$
のように,強め合いの条件のような形を得ることができます.
なんだか紛らわしいね.

位相差で強め合いの条件,弱め合いの条件を立てると,統一的に表現できます.
次回の内容はこちらです.


コメント
[…] […]
[…] https://physicmath.net/6001/,6001,physicmath.net投稿,publish 波動演習問題(標準)高校物理 シェアする Twitter Facebook はてブ LINE physicmathをフォローする physicmath Physicmath(フィジクマス) […]