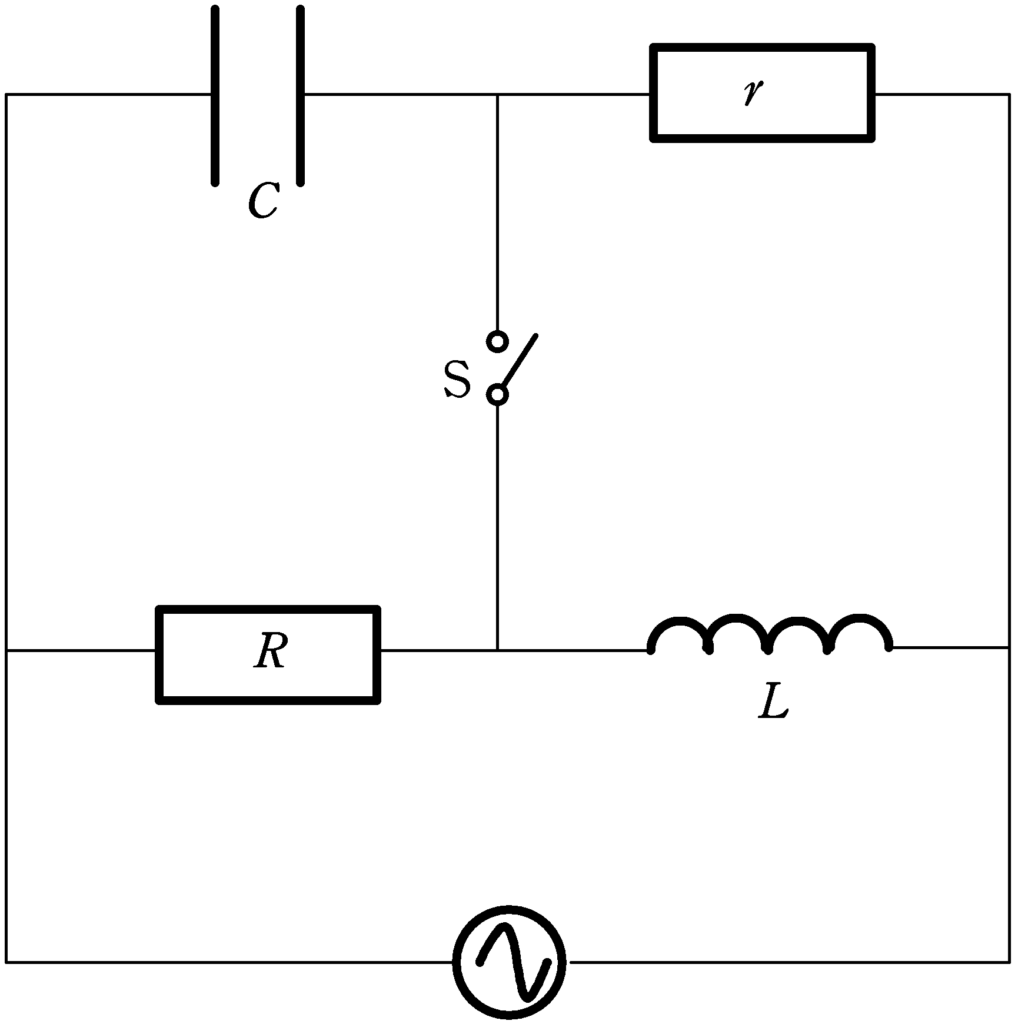

今回は,交流ブリッジの問題について考えてみたいと思います.
抵抗$R$と$r$の2つの抵抗と電気容量$C$のコンデンサー,自己インダクタンス$L$のコイル,スイッチS,交流電源を用いて,上図の回路をつくってみます.
そして,スイッチSを閉じたときに「スイッチSに流れる電流が$0$」のとき,自己インダクタンス$L$が$R,r,C$を用いてどのように表すことができるかを考えていきます.
交流の基礎知識として,次のことはおさえておいてください.
また,交流に関しては,こちらで,基本演習の問題もあります.
● 最大値について
回路素子にかかる電圧の最大値を$V_{0}$,流れる電流の最大値を$I_{0}$,リアクタンス(または抵抗)を$Z$とする.
このとき,次の関係が成り立つ.
$V_{0}=ZI_{0}$
$Z$は回路素子できまる.各周波数を$\omega$として
抵抗値$R$の抵抗のとき,$Z=R$
電気容量$C$のコンデンサーのとき,$Z=\dfrac{1}{\omega C}$
自己インダクタンス$L$のコイルのとき,$Z=\omega L$
● 位相のずれについて
1)電圧に対する電流の位相のずれ
抵抗:位相のずれはなし(オームの法則がいつでも成り立つ)
コンデンサー:$\dfrac{\pi}{2}$進む(電流が先に変化し,遅れて電荷が変化する)
コイル:$\dfrac{\pi}{2}$遅れる(電圧が先に変化し,遅れて電流が変化する)
2)電流に対するで電圧の位相のずれ
抵抗:位相のずれはなし(オームの法則がいつでも成り立つ)
コンデンサー:$\dfrac{\pi}{2}$遅れる(電流が先に変化し,遅れて電荷が変化する)
コイル:$\dfrac{\pi}{2}$進む(電圧が先に変化し,遅れて電流が変化する)
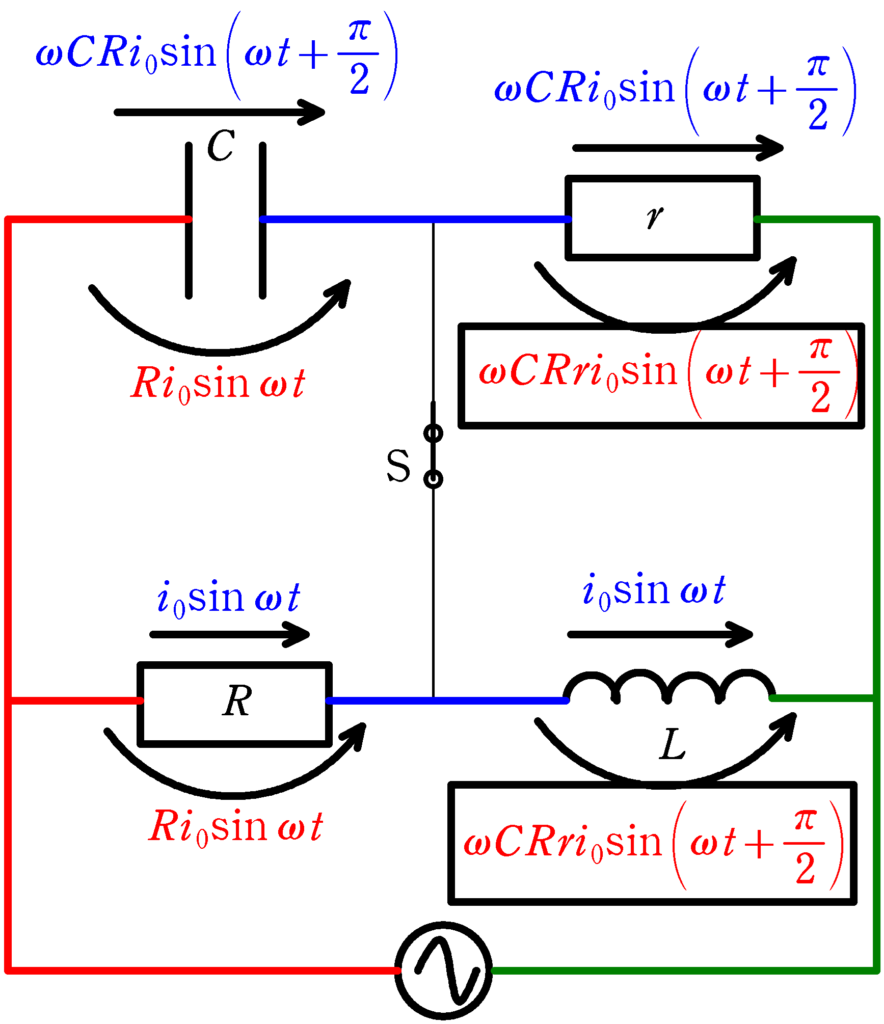
※ 図は電流が青色の文字,電圧が赤色の文字で書かれています.
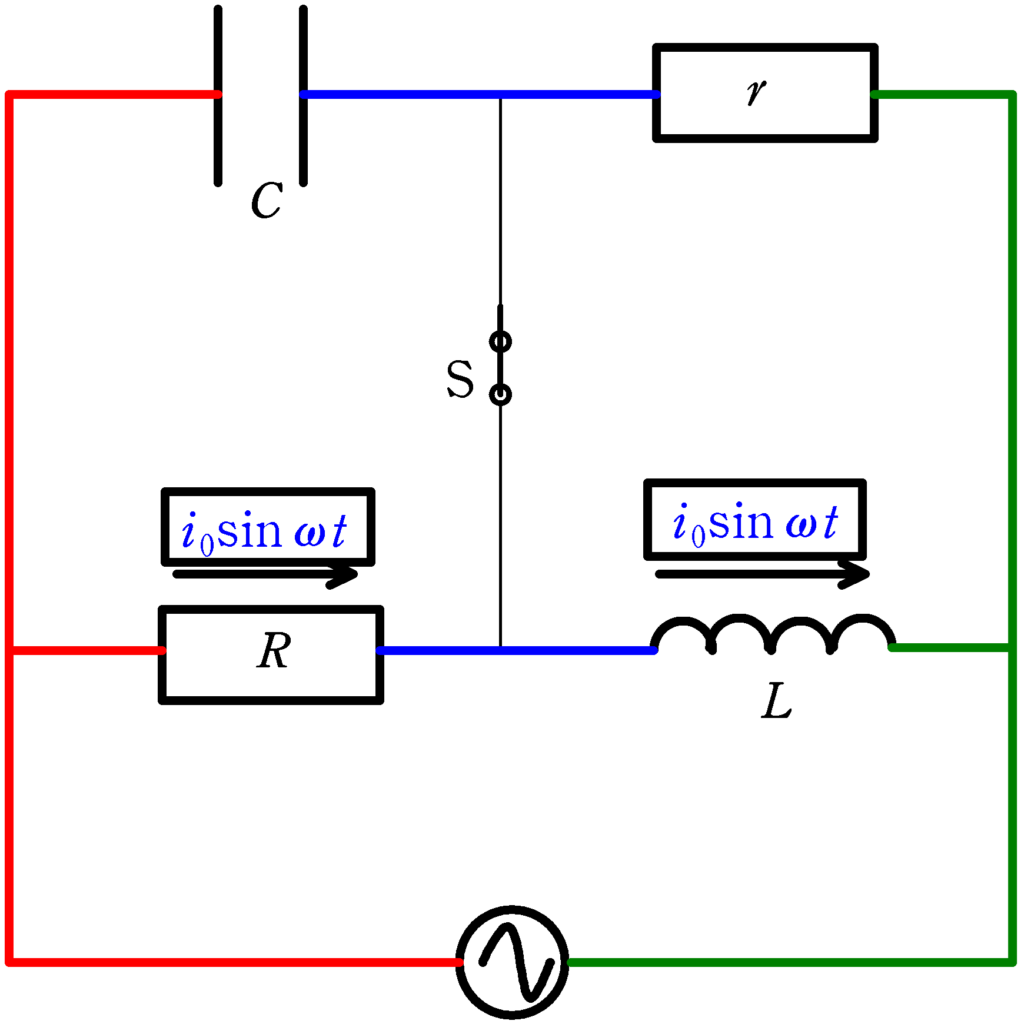

まず,設定からいきましょう.(上図をみてください.)
抵抗$R$に流れる電流を$i_{0}\sin\omega t$としましょう.$i_{0}$は正の定数で,$\omega$は角振動数です.すると,スイッチSには電流が流れないので,キルヒホッフ第1法則より,コイルに流れる電流も$i_{0}\sin\omega t$となります.
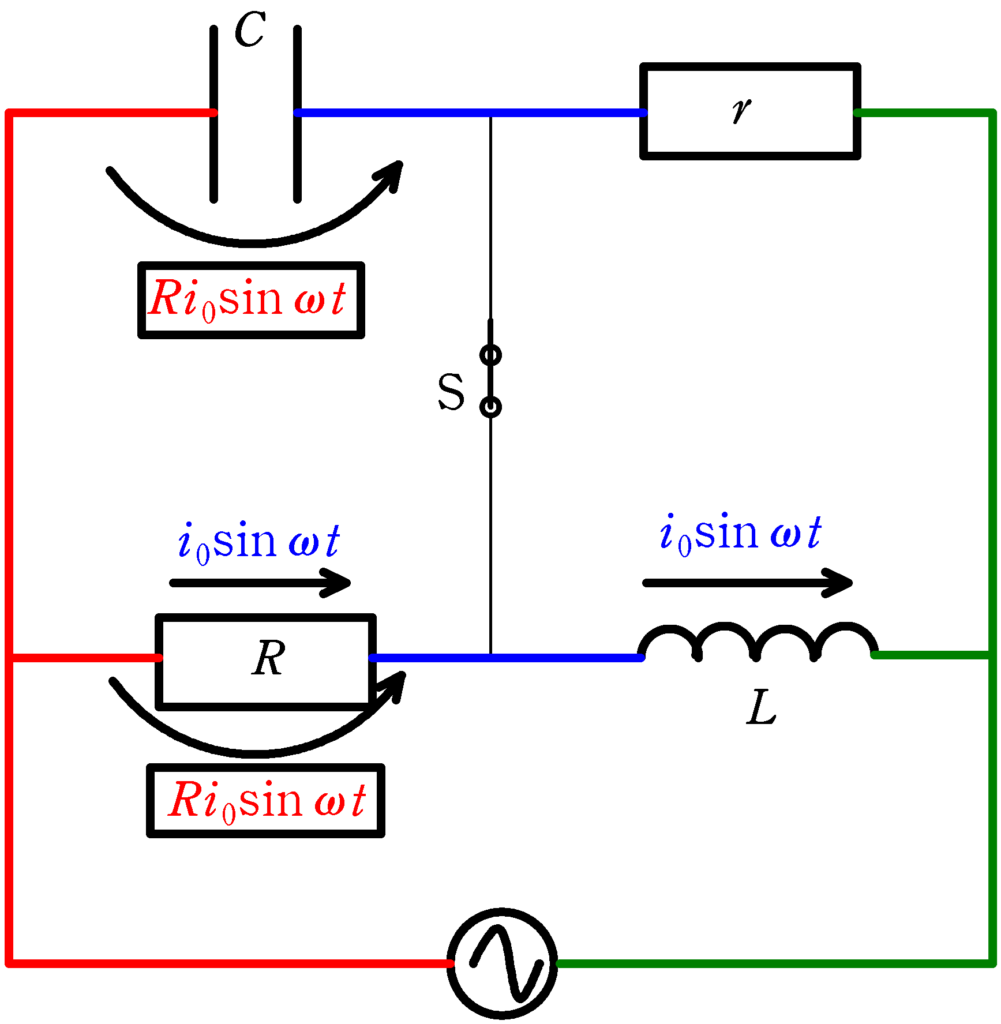

抵抗$R$に流れる電流が$i_{0}\sin\omega t$なので,抵抗$R$にかかる電圧の最大値を$V_{\rm R0}$とすると,
$V_{\rm R0}=R\times i_{0}$

が成り立ち,抵抗に流れる電流と電圧は位相(振動のタイミング)が等しいので,抵抗$R$の電圧の時間変化は
$Ri_{0}\sin\omega t$

となります.
さらに,スイッチSに電流が流れないということは,抵抗値$R$の抵抗にかかる電圧とコンデンサーにかかる電圧は等しくなります.
したがって,コンデンサーにかかる電圧も次のようになります.
$Ri_{0}\sin\omega t$
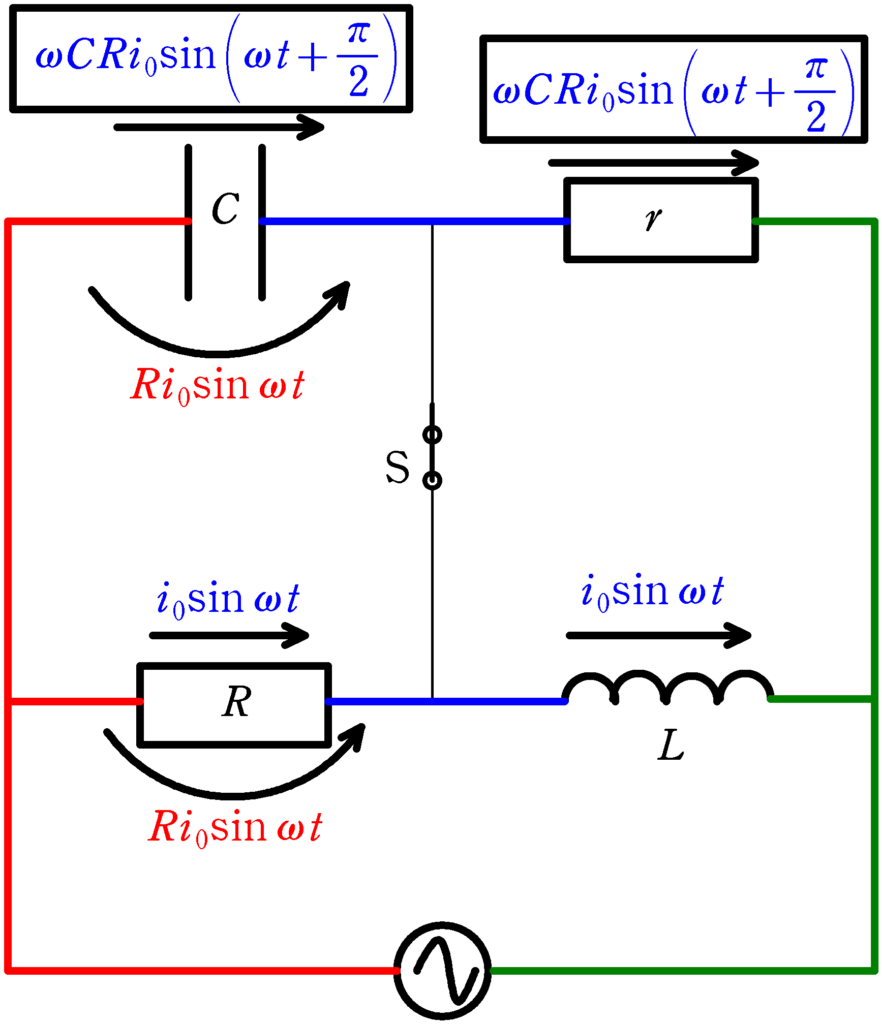

コンデンサーの電圧がわかったら,コンデンサーに流れる電流も計算できます.コンデンサーにかかる電流の最大値を$i_{\rm C0}$とすると,コンデンサーのリアクタンスは$\dfrac{1}{\omega C}$なので
$Ri_{0}=i_{\rm C0}\times \dfrac{1}{\omega C}$
$\therefore\,\, i_{\rm C0}=\omega CRi_{0}$

となります.
また,コンデンサーについて,「電圧に対する電流の位相は$\dfrac{\pi}{2}$進んでいる」のでコンデンサーに流れる電流は
$\omega CRi_{0}\sin\left(\omega t+\dfrac{\pi}{2}\right)$

となります.
さらに,スイッチSに電流が流れないので,キルヒホッフ第1法則より,コンデンサーに流れる電流と抵抗$r$に流れる電流も同じになります.

抵抗$r$に流れる電流が
$\omega CRi_{0}\sin\left(\omega t+\dfrac{\pi}{2}\right)$
とわかったので,今度は抵抗$r$にかかる電圧が計算できます.
抵抗$r$にかかる電圧の最大値を$V_{\rm r0}$とすると
$V_{\rm r0}=r\times \omega CRi_{0}=\omega CRri_{0}$

抵抗は電流と電圧の位相が等しいので,抵抗$r$にかかる電圧は
$\omega CRri_{0}\sin\left(\omega t+\dfrac{\pi}{2}\right)$
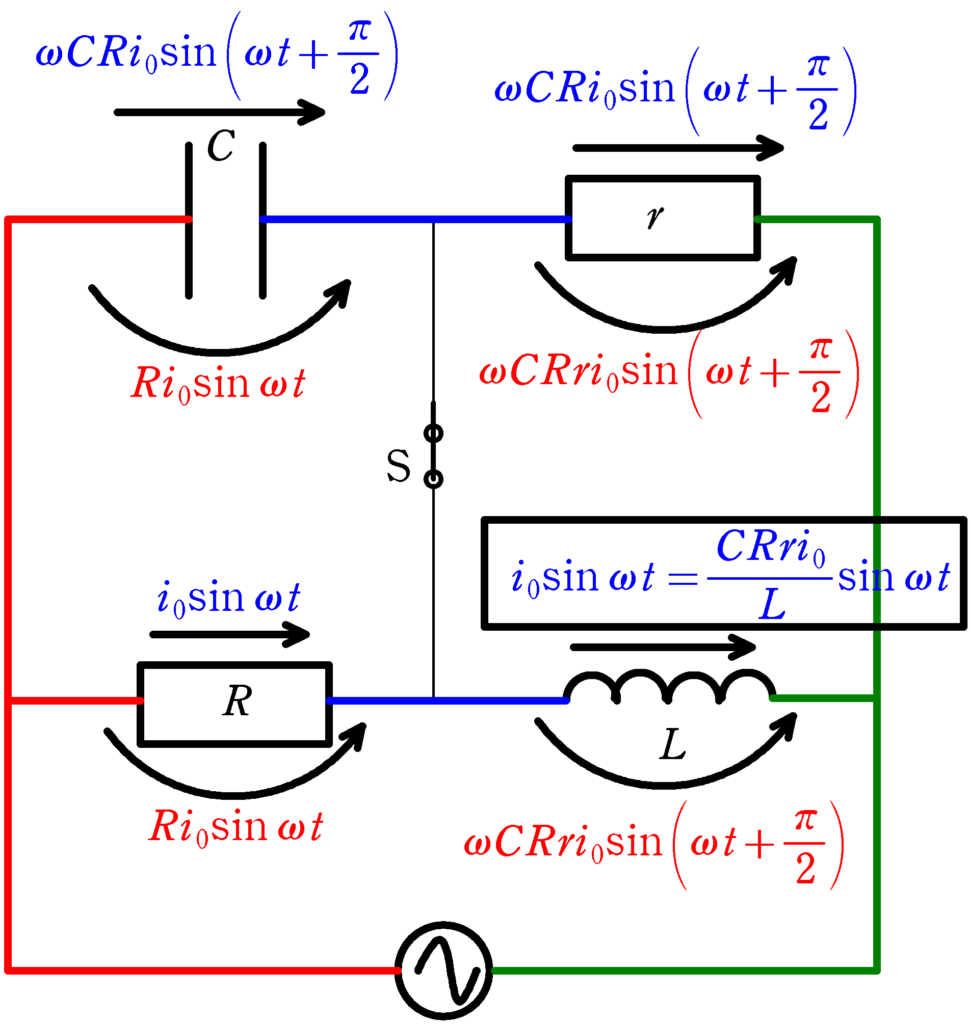

さらに,抵抗$r$とコイルにかかる電圧は等しいので,今度はコイルに流れる電流を計算できます.コイルに流れる電流の最大値を$i_{\rm L0}$とすると
$\omega CRri_{0}=\omega L\times i_{\rm L0}$
$\therefore\,\, i_{\rm L0}=\dfrac{CRri_{0}}{L}$

コイルの電圧に対する電流の位相は$\dfrac{\pi}{2}$遅れているので
コイルに流れる電流は
$\dfrac{CRri_{0}}{L}\sin\omega t$

となります.これは$i_{0}\sin\omega t$と等しいので,最大値部分を比較すると
$\dfrac{CRri_{0}}{L}=i_{0}$ $\,\,\therefore\,\,L=CRr$

となり,自己インダクタンスを求めることができました.
いまは,位相も含めて考察していきましたが,スイッチSに電流に電流が流れないときは,最大値の部分だけに着目しても計算ができます.ただ,大学入試で出題されるときは,誘導つきのことも多いので,位相も含めてどのように計算できるのかを追っていくところから始めた方がよいでしょう.

コメント