
重力だけがはたらく運動の場合,水平面から鉛直真上に投げ上げると,
水平面から最高点に達するまでの時間(行きの時間)=最高点から再び地面に帰ってくるまでの時間(帰りの時間)
ということはよく知られていると思います.
今回は,速さに比例する空気抵抗がはたらく場合,「行きの時間」と「帰りの時間」の大小関係はどのようになるのかを考察していきたいと思います.
微分方程式を解き,考察するのはかなりやっかいなので,過去に福島県立医科大で出題されたような$v-t$グラフを用いた考察をしていきたいと思います.
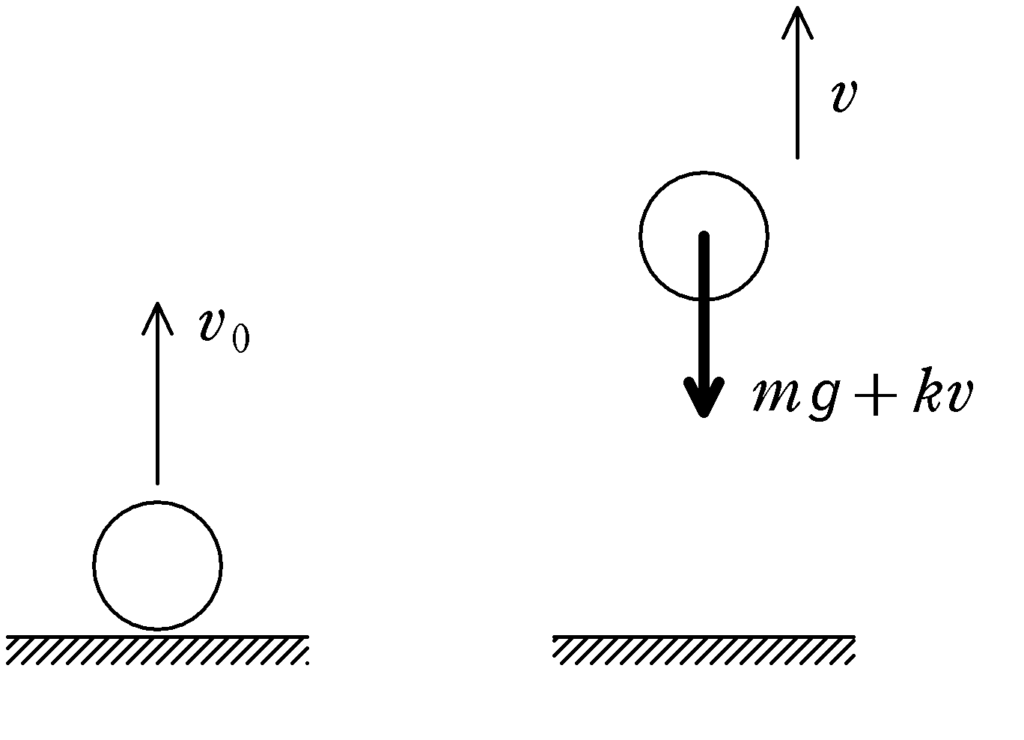

まずは,どのような$v-t$グラフになるか調べるために運動方程式を立てていきたいと思います.
鉛直分上向きを正とし,速度$v$,加速度$a$を設定します.物体の質量は$m$,初速度は$v_{0}\,(>0)$としましょう.重力加速度の大きさを$g$とすると,重力の大きさは$mg$で鉛直下向きにはたらきます.
また,たとえば,物体が正の速度を持っているとき,空気抵抗は比例定数を$k$として,鉛直下向きに$kv$がはたらきます.したがって,運動方程式は次のようになります.
$ma=-mg-kv$ $\therefore\,\, a=-\dfrac{k}{m}\left(v+\dfrac{mg}{k}\right)$ $\cdots (\ast)$

でもこれって物体の速度が負の場合は空気抵抗が鉛直上向きにはたらくからまずいんじゃない?

いえ,物体の速度の正負に関わらず,運動方程式の形は変わりません.物体の負の速度を持っている場合は,空気抵抗は正の方向に大きさ$k|v|=k\times (-v)$がはたらきます.
$ma=-mg+k|v|=-mg-kv$

なるほど!摩擦力がはたらくときとは違って,速度の向きが変わっても統一的な式がかけるんだね.

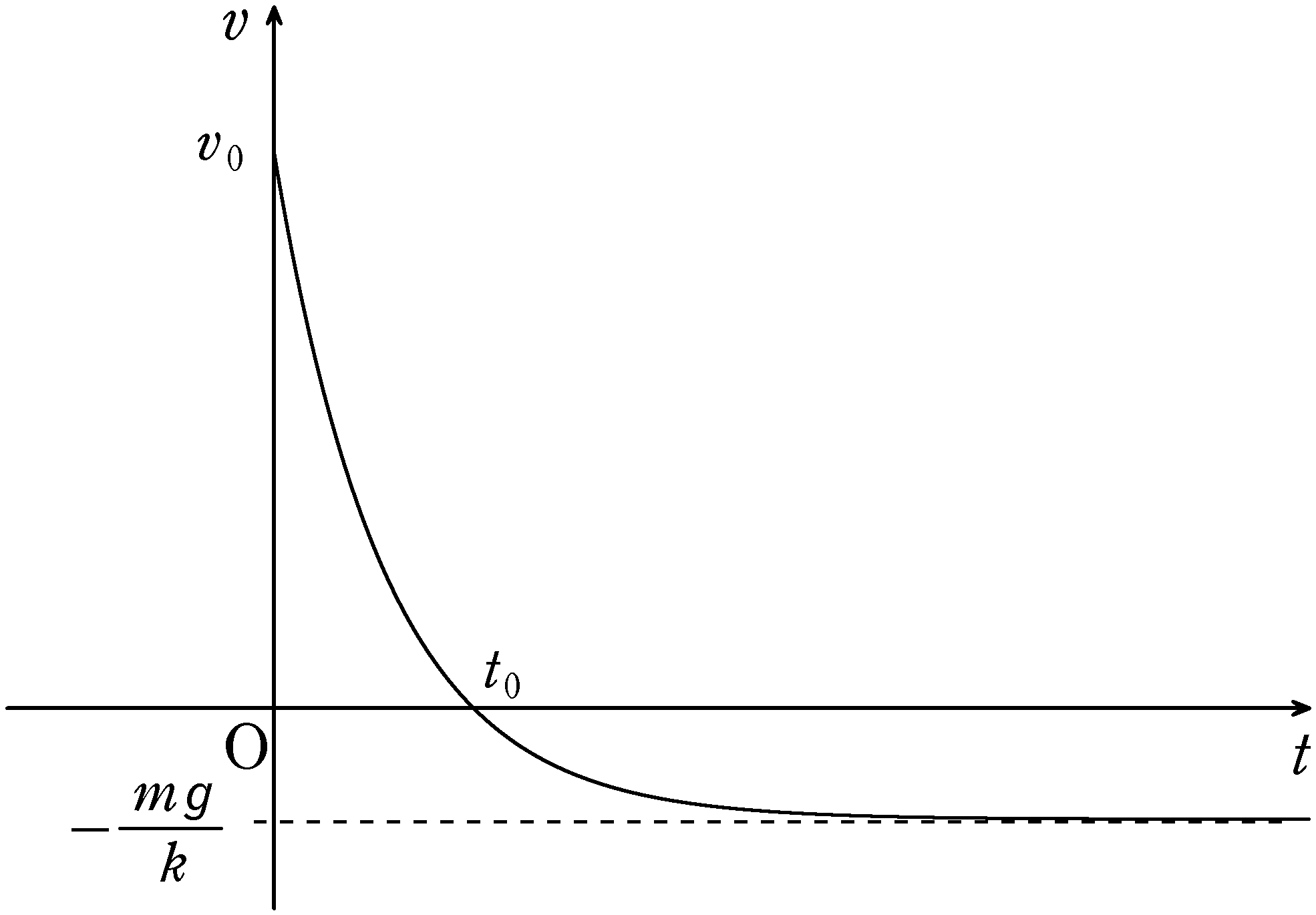
さて,$v-t$グラフの傾きは加速度$a$に対応していることに着目すると$(\ast)$の式から,投げ上げたときの$v=v_{0}$のときは加速度は$a=-\dfrac{k}{m}\left(v_{0}+\dfrac{mg}{k}\right)$で,だんだんと速さが遅くなっていきます.
$a=0$になるのは
$v+\dfrac{mg}{k}=0$ $\therefore\,\, v=-\dfrac{mg}{k}$

なので,「行き」の時点では終端速度に達しません.最高点に達して速度が$0$になったあと,負の速度に転じ,そのあとだんだんと終端速度$v=-\dfrac{mg}{k}$に近づいていきます.
これをもとに$v-t$グラフは次のようになります.
最高点に達した時刻は$t_{0}$としています.
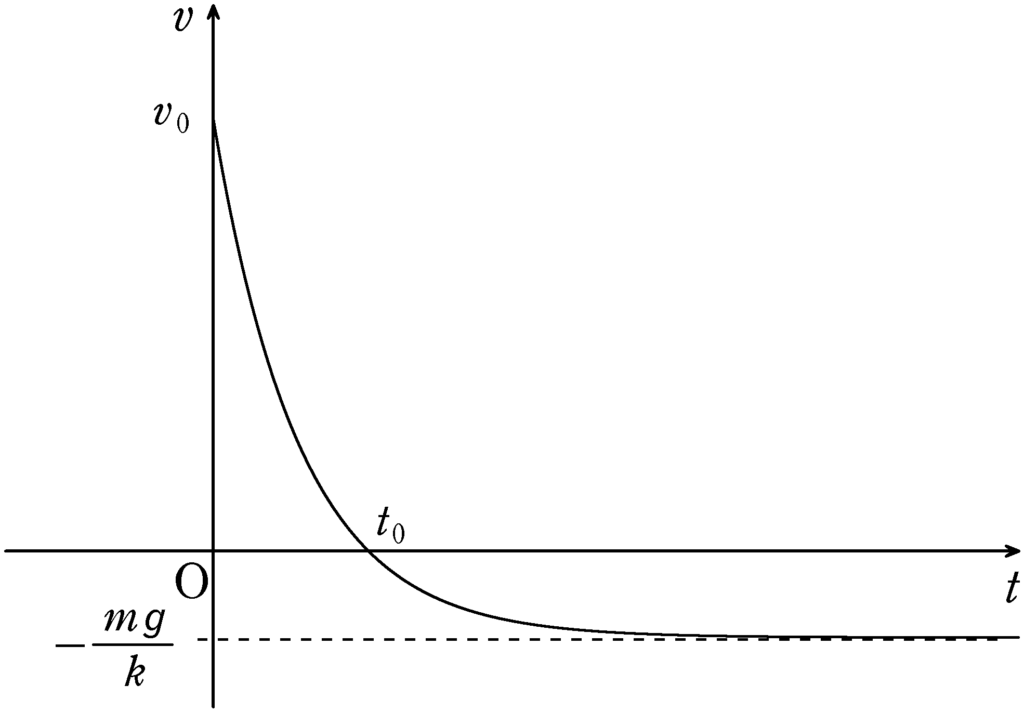

このままでは,「行き」と「帰り」の時間どちらが短いかわからないね.

はい.そこで,「空気抵抗がはたらかない場合の物体の運動」をあえて考えていきたいと思います.
その際,空気抵抗がはたらく場合の最高点に達する時刻$t_{0}$と「空気抵抗がはたらかない場合の物体の運動」が最高点に達する時刻と高さが一致するように「空気抵抗がはたらかない場合の物体の運動」の初速度と投げ上げる時刻を調整します.
空気抵抗がはたらかない場合は,加速度が$-g$なので,直線になり,次のように$v-t$グラフをかくことができます.
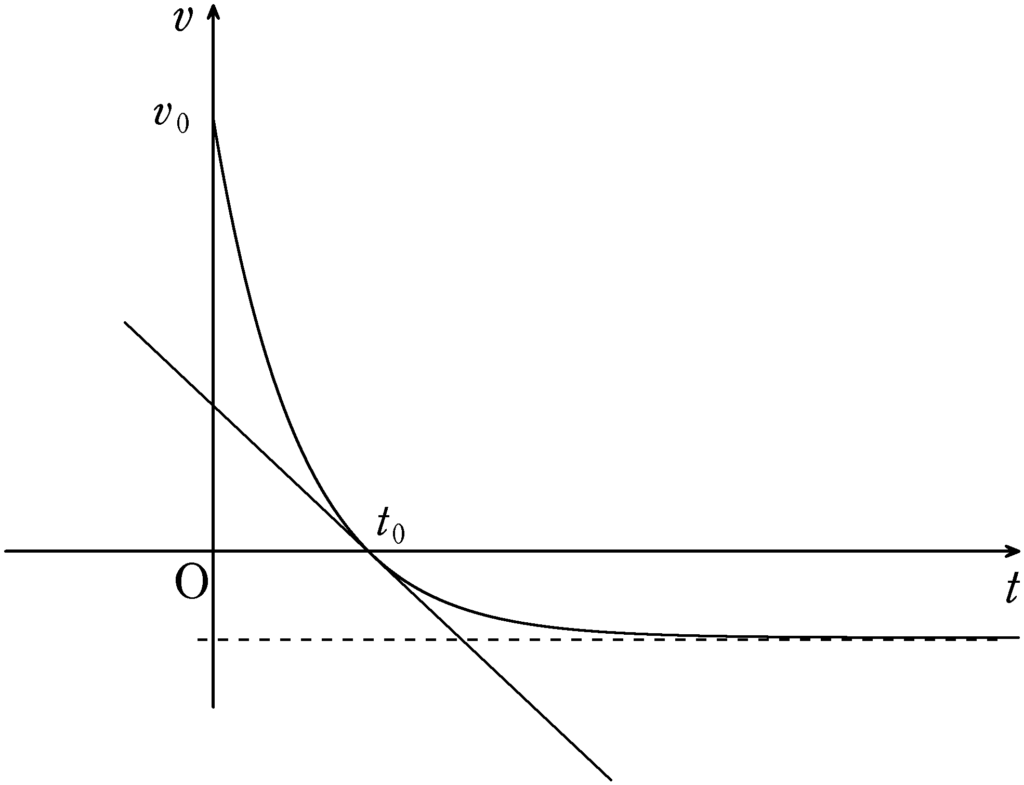

$t=t_{0}$で曲線と直線は必ず接するの??

はい.最高点では,空気抵抗がはたらく場合も速度が$v=0$なので,加速度が$-g$になり,「空気抵抗がはたらかない場合の物体の運動」の加速度と同じになります.だから,$t=t_{0}$で傾きが同じになるわけです.

空気抵抗がはたらく場合も「空気抵抗がはたらかない場合の物体の運動」でも行きの移動距離は同じ(ように設定した)なので$v-t$グラフの面積は同じにならなければいけません.
すると,「空気抵抗がはたらかない場合の物体の運動」では,空気抵抗がはたらく場合よりも早めに物体を投げ出さなければならないことに気づきます.
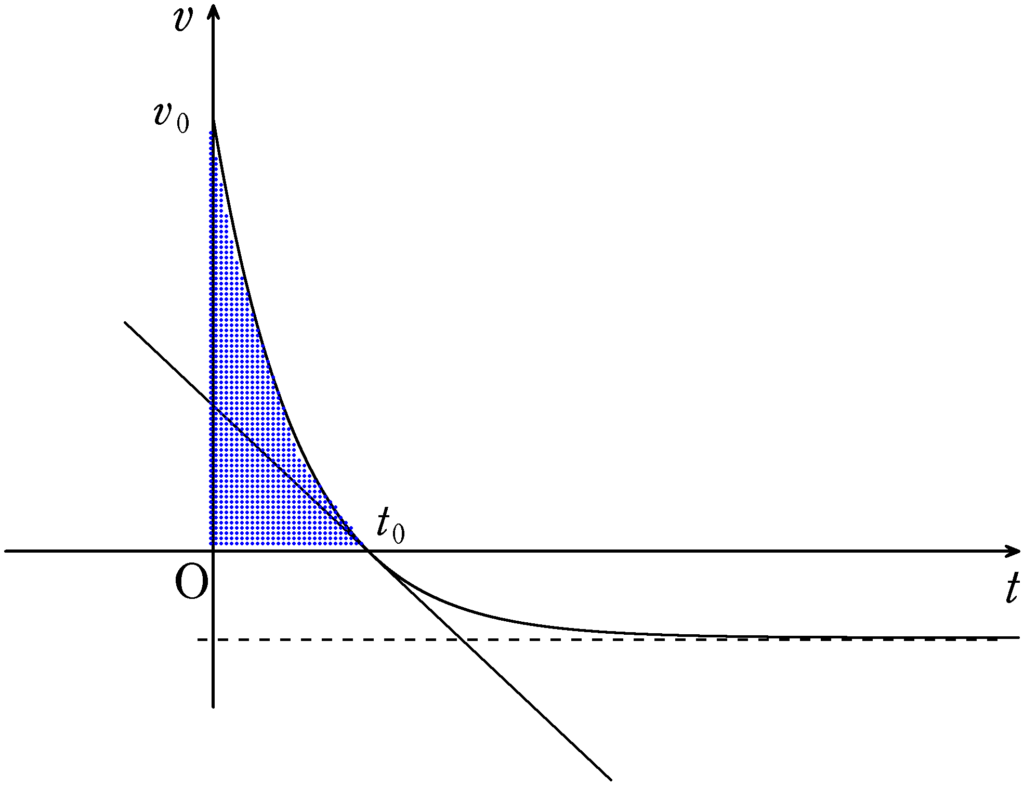
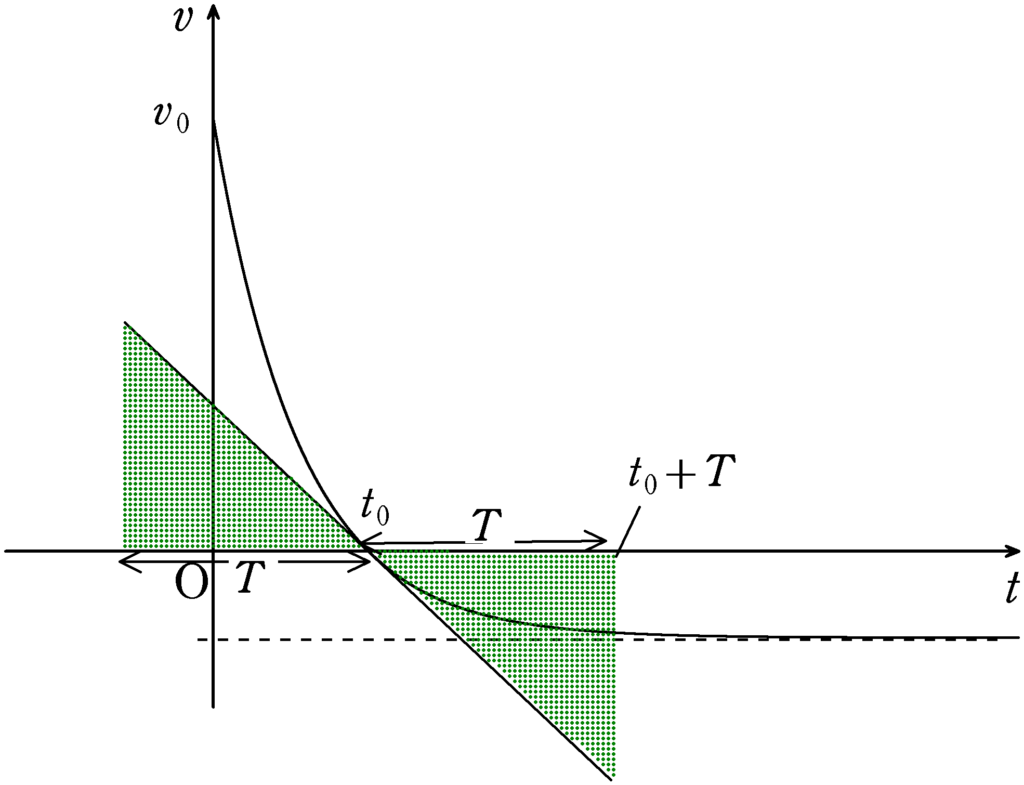

つまり,「空気抵抗がはたらかない場合の物体の運動」の行きの時間$T$と空気抵抗がはたらく場合の行きの時間$t_{0}$は
$t_{0}<T$
というわけだね.
「空気抵抗がはたらかない場合の物体の運動」では,帰りの時間も上図のように$T$になるね.

はい.そして,帰りの移動距離を考えると,上図の緑色の面積(直角三角形の面積)同じ面積になるには,空気抵抗がはたらく場合の帰りの時刻は$t_{0}+T$より遅くならなくてはいけません.
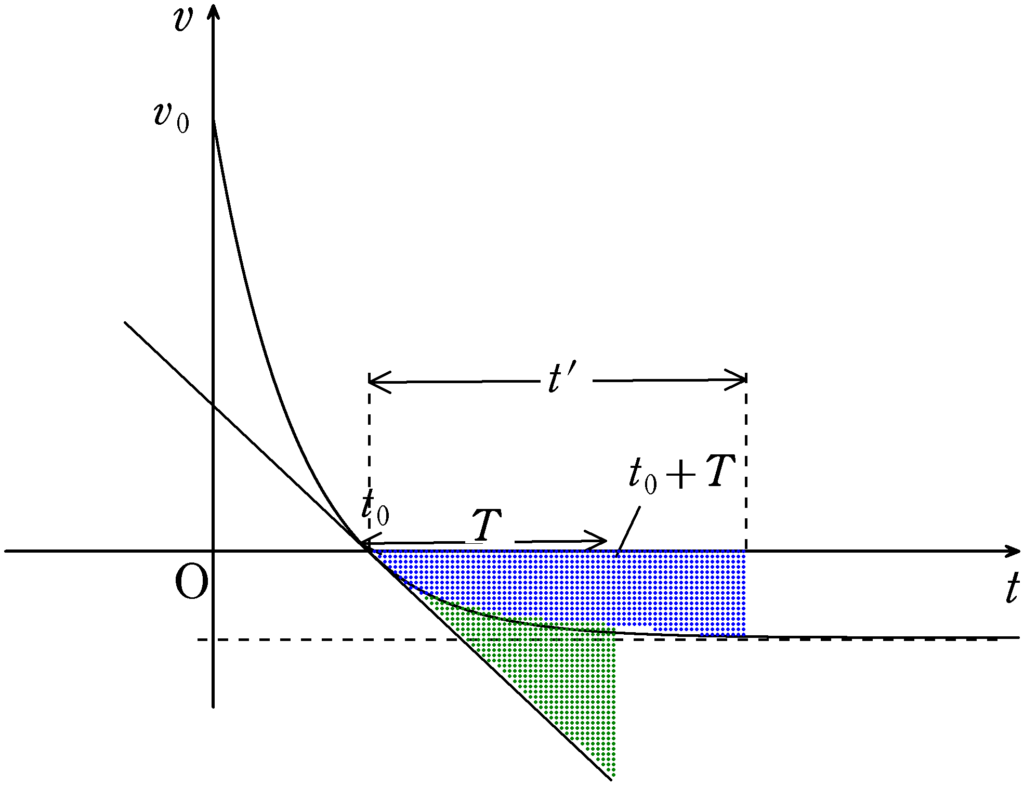

空気抵抗がはたらく場合の帰りの時間を$t’$とすると,$T<t’$となるんだね.
つまり,$t_{0}<T$も合わせて考えれば
$t_{0}<T<t’$
となって,空気抵抗がはたらく場合の「行き」の時間と「帰り」の時間は「行き」の時間の方が短くなるわけだね.


コメント