<問題>

<解答>
こちらでも類題を扱っています.
まずは,スイッチ$\rm S_{1}$を閉じて十分時間が経つと,電気容量$C$のコンデンサーの電圧と直流電源の電圧が等しくなる.コンデンサーの基本式より,蓄えられてた電荷$Q_{0}$は
$Q_{0}=CE_{0}$ $\cdots (\ast)$
次に$\rm S_{1}$を開いて$\rm S_{2}$を閉じると電気振動がはじまる.ここで気をつけて欲しいのが,コイルに流れる電流が最大になるときは,コンデンサーの電圧は$0$(蓄えられている電荷が$0$)というわけではないということ.基本的な$LC$振動回路が「(電流が最大になるとき)=(コンデンサーの電荷が0のとき)」なので勘違いしやすい.
電流が最大になるのは,「電流の時間変化が$0$のとき」である.
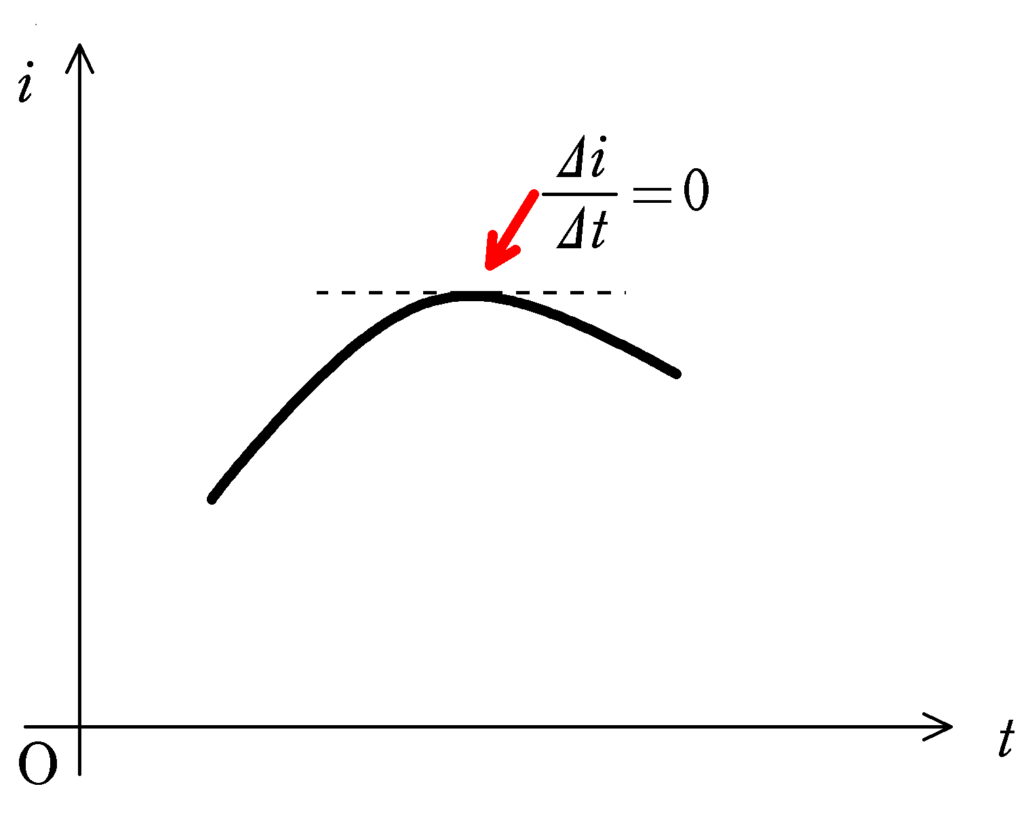
このとき,上図のように,電流が最大になるのは,$i-t$グラフの傾きが$0$のときである.すると,コイルに生じる誘導起電力の大きさ$V_{L}$は
$V_{L}=L|\dfrac{\varDelta i}{\varDelta t}|$
なので,電流が最大になるのは,コイルの誘導起電力が0のときである.
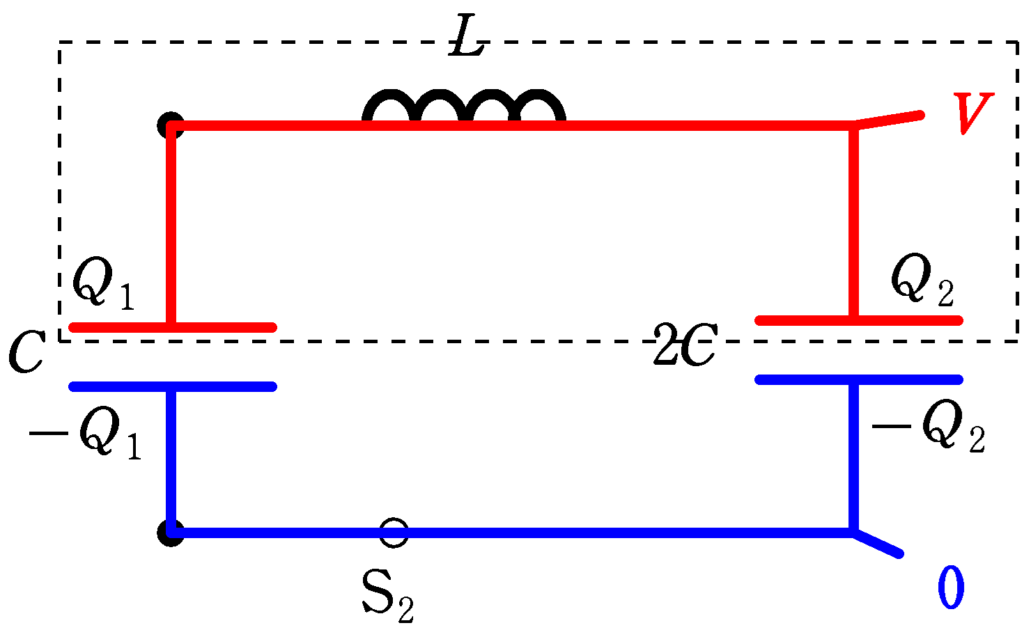
上図のように,電位,電荷を設定すると,$(\ast)$から,点線部分の電荷保存則より
$Q_{1}+Q_{2}=CE_{0}$ $\cdots (2\ast)$
また,コンデンサーの基本式より
$Q_{1}=CV$, $Q_{2}=2CV$ $\cdots (3\ast)$
$(3\ast)$を$(2\ast)$に代入して,$V$を求めると
$CV+2CV=CE_{0}$ $\therefore\,\,V=\dfrac{E_{0}}{3}$
したがって,電流が最大になるとき,コンデンサーの静電エネルギーの和$U_{\rm C}$は
$U_{\rm C}=\dfrac{1}{2}C\left(\dfrac{E_{0}}{3}\right)^{2}+\dfrac{1}{2}\cdot 2C\left(\dfrac{E_{0}}{3}\right)^{2}=\dfrac{1}{6}CE_{0}^{2}$
となる.電流の最大値を$I$として,$\rm S_{2}$を閉じた直後と電流が最大になるときでエネルギー保存則を立てると
$\dfrac{1}{2}CE_{0}^{2}=\dfrac{1}{6}CE_{0}^{2}+\dfrac{1}{2}LI^{2}$
$\therefore\,\, I=E_{0}\sqrt{\dfrac{2C}{3L}}$ (答)


コメント