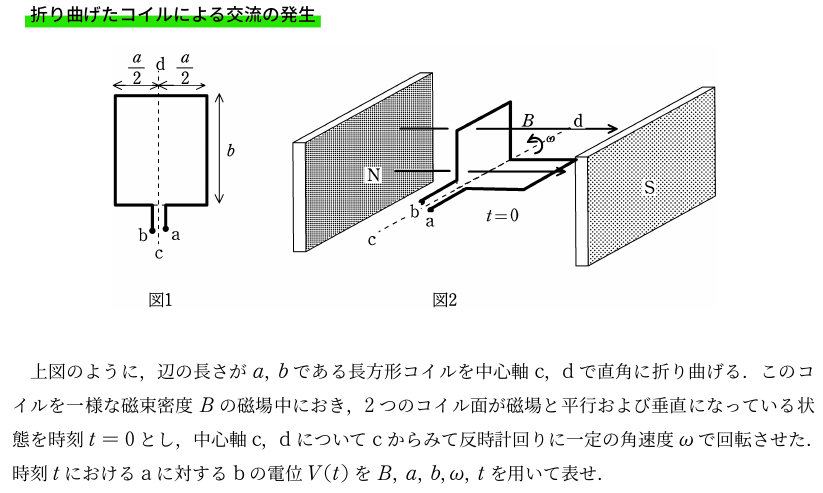
<問題>
<解答>
$V=\dfrac{\varDelta \varPhi}{\varDelta t}$を用いて計算もできるが,ここでは,導体棒が磁場中を動くときの誘導起電力を用いて計算する.
PQ間に生じる誘導起電力の大きさ$V_{\rm{PQ}}$は,PQの長さを$l$,PQ方向に垂直な速さを$v_{\perp}$,導体棒が動く方向と垂直な磁束密度の大きさを$B$とすれば,
$V=v_{\perp}Bl$
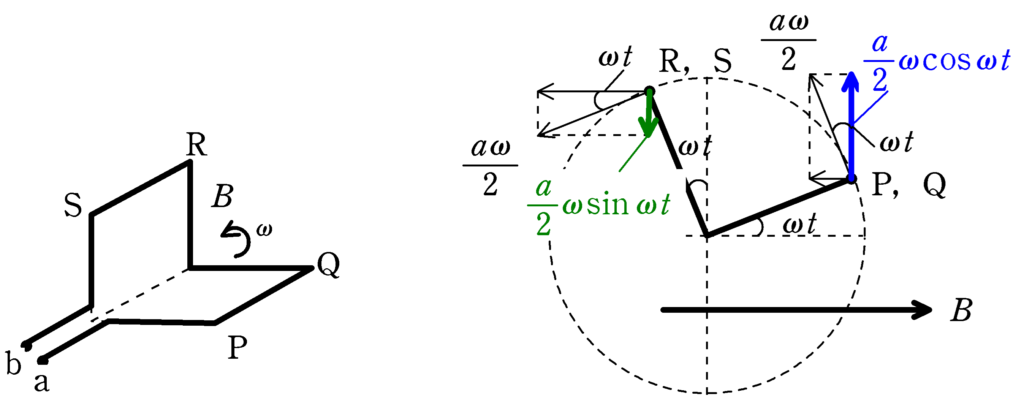
上図のようにP,Q,R,Sを定め(左上図),時刻$t$において角度$\omega t$回ったときについて考える.(右上図)
中心軸からP,QやS,Rまでの距離は$\dfrac{a}{2}$だから,円運動の半径と角速度と速さの関係より,PQ部分とSR部分はどちらも
$\dfrac{a}{2}\omega$
の速さで動いている最中である.
導体棒が磁場中を動いていると誘導起電力が生じる.その際,磁束密度に垂直な速度成分が誘導起電力に関係のあるものであるから,上図のように,PQ部分,SR部分の速度の磁束密度に垂直な成分を求めると,$\dfrac{a}{2}\omega\cos\omega t$,$\dfrac{a}{2}\omega\sin\omega t$となる.
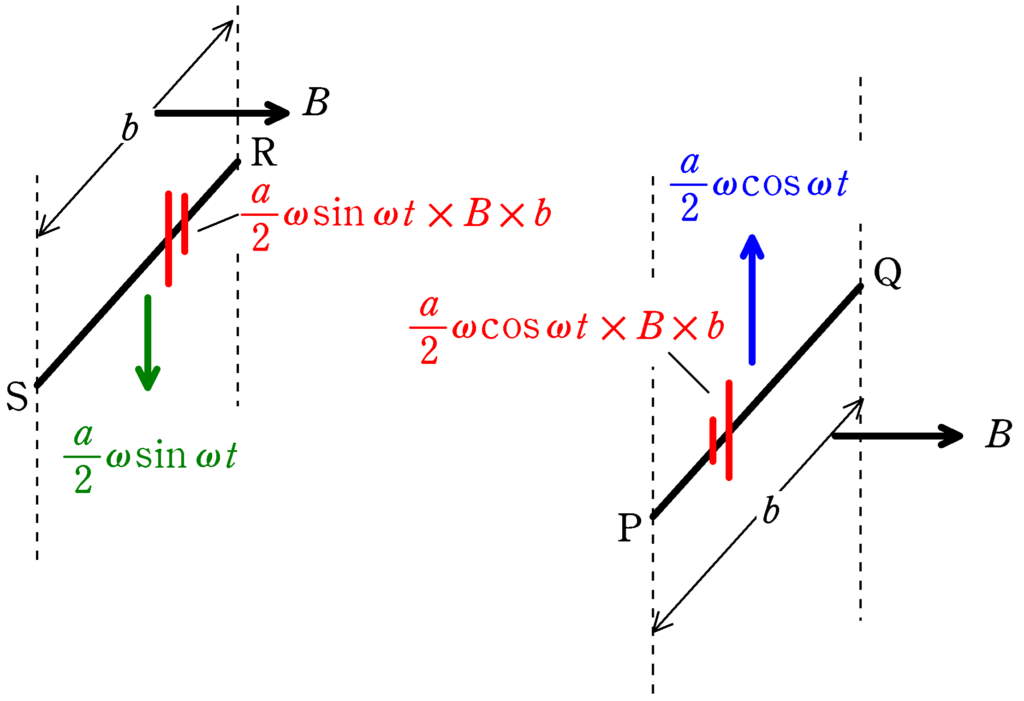
まず,導体棒PQについて,磁束密度が図の右向きで,導体棒が磁場を垂直に切る速度が$\dfrac{a}{2}\omega \cos \omega$で,PQの長さが$b$なので,誘導起電力は
$\dfrac{a}{2}\omega\cos\omega t\times B\times b=\dfrac{Bab\omega }{2}\cos\omega t$
となる.同様に考えて,SR部分の導体棒に生じる起電力は
$\dfrac{Bab\omega }{2}\sin\omega t$
となる.誘導起電力の向きはレンツの法則(またはローレンツ力がはたらく向きで起電力の向きを調べる)で決まる.
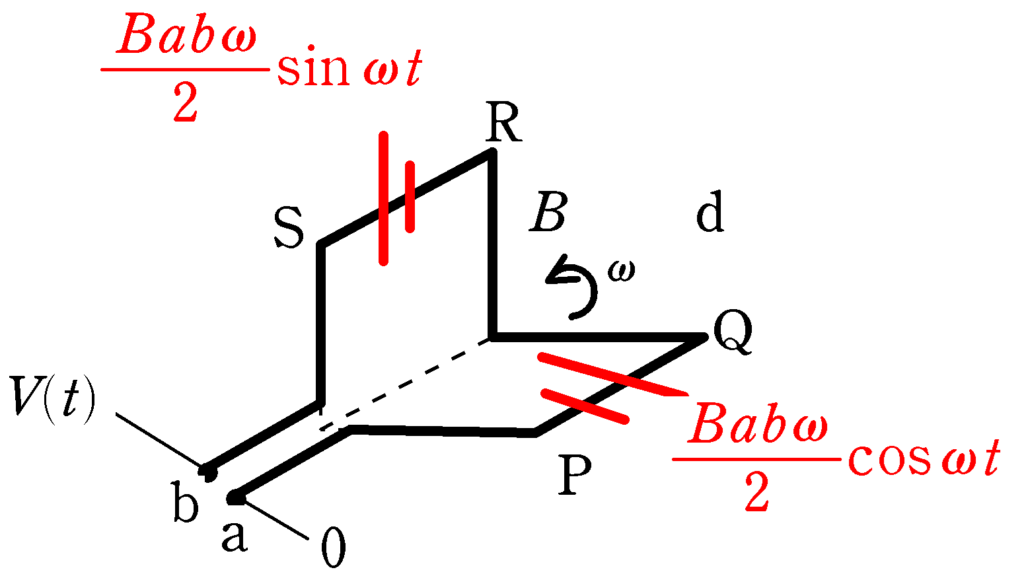
したがって,aに対するbの電位はキルヒホッフの法則より
$\eqalign{V(t)&=\dfrac{Bab\omega}{2}\sin\omega t+\dfrac{Bab\omega}{2}\cos\omega t\\&=\dfrac{Bab\omega}{2}(\sin\omega t+\cos\omega t)\\&=\dfrac{\sqrt{2}Bab\omega}{2}\sin\left(\omega t+\dfrac{\pi}{4}\right)}$
となる.(答)
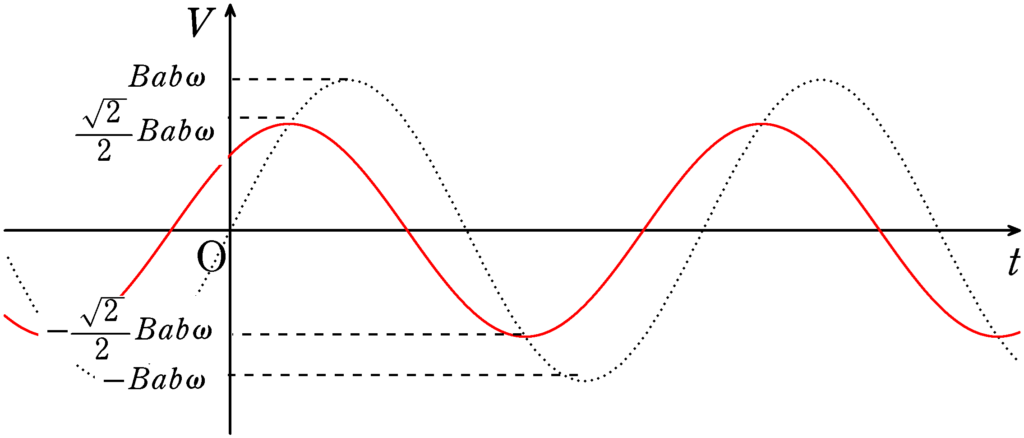
ちなみに,コイルを折り曲げないで,コイル面が磁場を垂直に貫く位置から回転させた場合は電位が$V(t)=Bab\omega \sin\omega t$になります.折り曲げる前(点線)と折り曲げた後(赤い実線)の時刻$t$と電位$V$のグラフは下図のようになります.




コメント