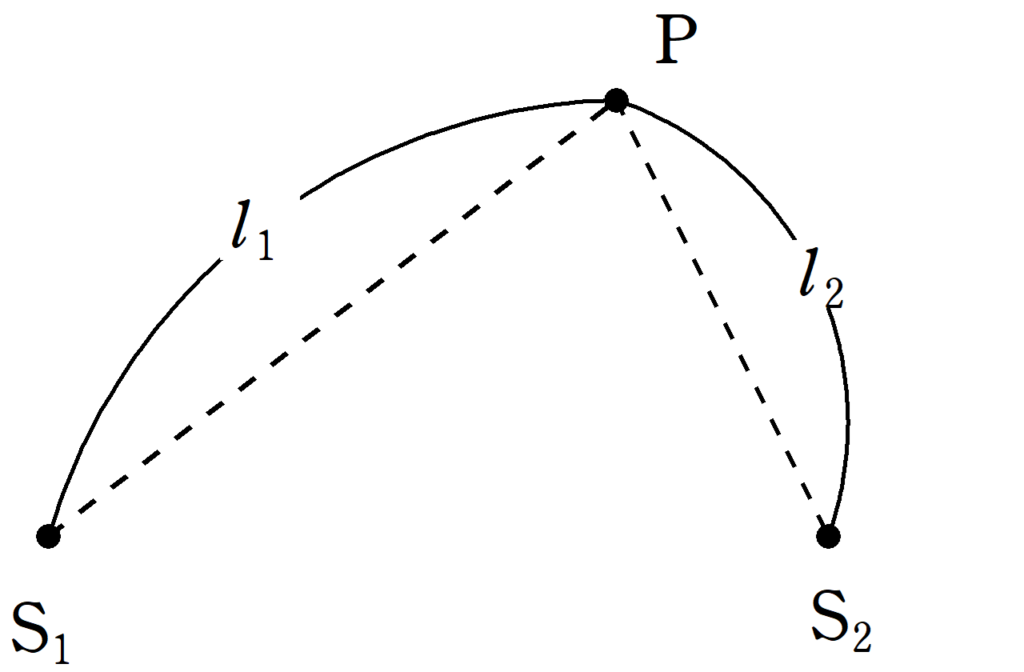
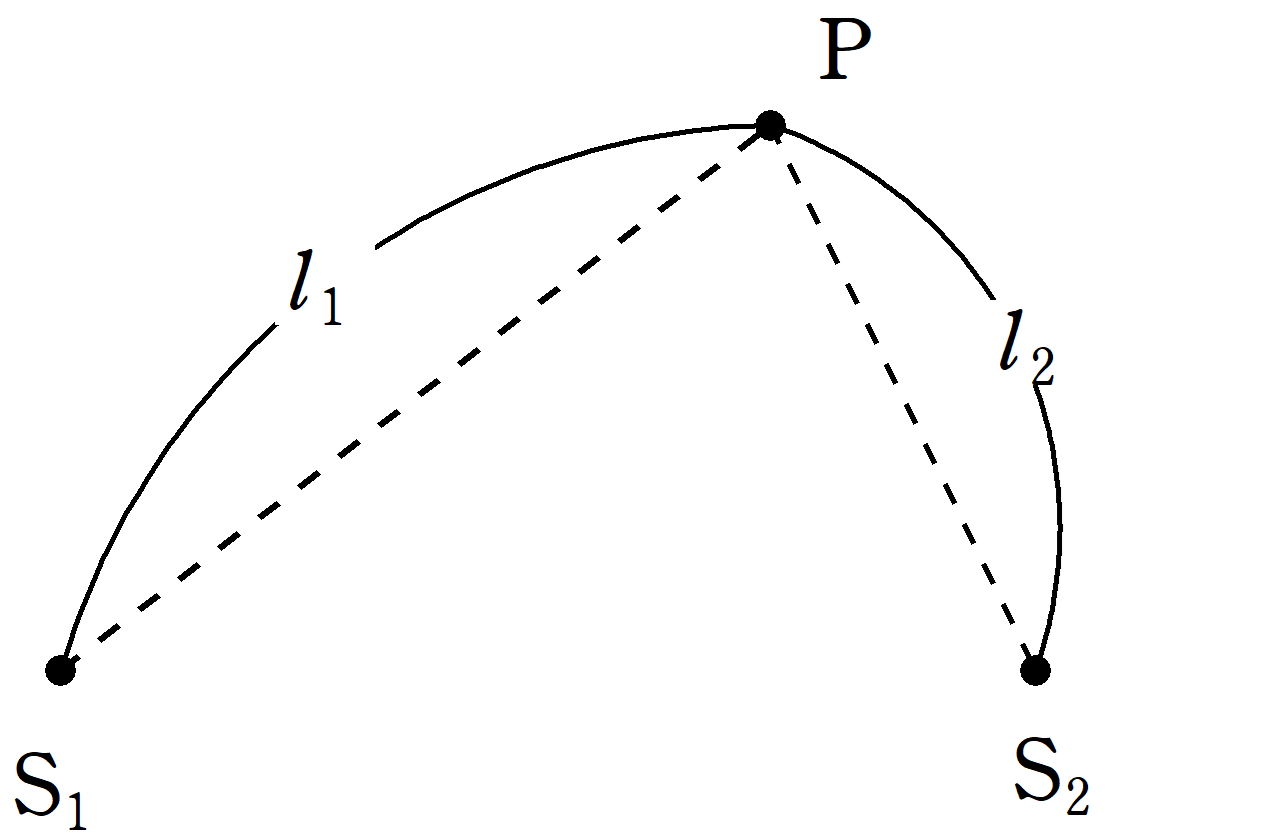
波源$\rm S_{1}$，$\rm S_{2}$があり，波源$\rm S_{1}$では時刻$t$において，$y_{1}=A\sin\left(2\pi ft\right)$で振動していて，波源$\rm S_{2}$では，$y_{2}=A\sin\left(2\pi ft\right)$で振動している．ただし，$A$は振幅，$f$は振動数であり，どちらも正の定数である．${\rm S_{1}P}=l_{1}$，${\rm S_{2}P}=l_{2}$であるような点$\rm P$がある．このとき，次の問いに答えよ．ただし，伝わる波の波長を$\lambda$とする．
(1) $\rm S_{1}$から$\rm P$に伝わる波の$\rm P$における媒質の変位と$\rm S_{2}$から$\rm P$に伝わる波の$\rm P$における媒質の変位の位相差$\varDelta \varphi$を$\lambda$，$l_{1}$，$l_{2}$を用いて表せ．
(2) 2つの波が強め合うときの条件を整数$k$および，$l_{1}$，$l_{2}$，$\lambda$を用いてかけ．
(3) 2つの波が弱め合うときの条件を整数$k$および，$l_{1}$，$l_{2}$，$\lambda$を用いてかけ．
＜解答＞
(1)
波が伝わる速さを$V$とすると，$\rm S_{1}$から$\rm P$に伝わる波において，$\rm P$で媒質の変位は，時間$\dfrac{l_{1}}{V}$前の$\rm S_{1}$での振動と等しいんだよね．
したがって，媒質の変位$y_{1\rm P}$は
$y_{1\rm P}=A\sin\left\{2\pi f\left(t-\dfrac{l_{1}}{V}\right) \right\}$
このとき，位相$\varphi_{1}$は，波の基本式，$V=f\lambda$も用いると次のようになります．
$\varphi_{1}=2\pi f\left(t-\dfrac{l_{1}}{V}\right)=2\pi ft-\dfrac{2\pi }{\lambda}l_{1}$
同じように，$\rm S_{2}$から$\rm P$に伝わる波の$\rm P$における媒質の位相$\varphi_{2}$は
$\varphi_{2}=2\pi f\left(t-\dfrac{l_{2}}{V}\right)=2\pi ft-\dfrac{2\pi }{\lambda}l_{2}$
したがって，位相差$\varDelta \varphi$は
$\varDelta \varphi=\varphi_{1}-\varphi_{2}=\dfrac{2\pi}{\lambda}(l_{2}-l_{1})$ （答）
(2)
強め合うのは，$\varDelta \varphi$が$2\pi$の整数倍になるときなので
$\varDelta \varphi=2\pi k$
$\therefore \dfrac{2\pi}{\lambda}(l_{2}-l_{1})=2\pi k$ (答)
さらに変形すると，
$l_{2}-l_{1}=k\lambda$
のように，よく見る強めいあいの条件が出てくるね．
(3)
弱め合うのは，$\varDelta \varphi$が$\pi$の奇数倍のときなので
$\varDelta \varphi=(2k-1)\pi$
$\therefore \dfrac{2\pi}{\lambda}(l_{2}-l_{1})=(2k-1)\pi $（答）
同様に，
$l_{2}-l_{1}=\left(k-\dfrac{1}{2}\right)\lambda$
を得ます．
コメント
[…] […]