
下の記事にある波の式の演習問題をやりたいな.
入試でもよく出てくるし・・・

そうですね.
それでは,波の式を立て方を上の記事を読んで復習しておいてください.
あと,自由端反射と固定端反射の問題を出すので,こちらも復習しておきましょう.

上の記事にも書いてあるけど,おおざっぱにまとめておこうね!
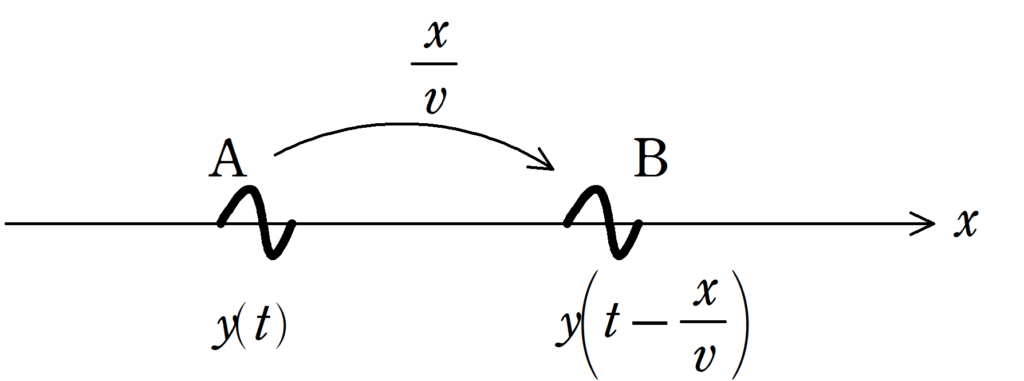
Aにおいて,媒質が単振動していて,その振動は$y_{\rm{A}}(t)$である.
波が伝わる速さが$v$でAからBの向きに波が伝わっているとする.
AB間の距離を$x$とすると,Aの振動がBの場所に伝えられるのにかかる時間は$\dfrac{x}{v}$である.
すると,Bの振動$y_{\rm{B}}(t)$は時間$\dfrac{x}{v}$前のAの振動と等しいので
$y_{\rm{B}}(t)=y_{\rm{A}}\left(t-\dfrac{x}{v}\right)$
・自由端反射では入射波と反射波の位相(タイミング)のずれはない.
・固定端反射では入射波と反射波の位相(タイミング)は$\pi$ずれる.

それでは解いてみましょう!
[1]
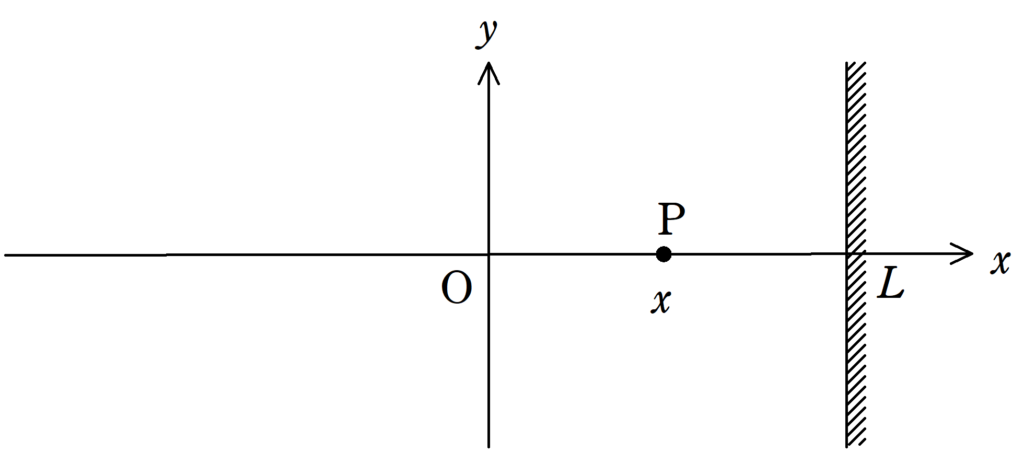
原点Oの時刻$t$における媒質の変位$y_{\rm{O}}(t)$が振幅$A$,周期$T$として
$y_{\rm{O}}(t)=A\cos\dfrac{2\pi}{T}t$
であった.この媒質の振動が速さ$v$で$x$軸の正の方向に伝わっている.
この波が媒質Pに直接伝わる入射波とPを通りすぎ,$x=L$において反射して再びPに伝わる反射波について次の問いに答えよ.
(1) 座標$x(x>0)$にある媒質Pに直接伝わる入射波の時刻$t$における波の変位$y_{\rm{P1}}(t)$の時間変化を求めよ.
(2) 座標$x(x>0)$にある媒質Pを通りすぎて$x=L$にある壁で反射された波が再びPにたどりついた.このとき,時刻$t$における媒質Pの反射波の変位$y_{\rm{P2}}(t)$の時間変化を求めよ.ただし,壁での反射は自由端反射とする.
(3) 座標$x(x>0)$にある媒質Pを通りすぎて$x=L$にある壁で反射された波が再びPにたどりついた.このとき,時刻$t$における媒質Pの反射波の変位$y_{\rm{P3}}(t)$の時間変化を求めよ.ただし,壁での反射は固定端反射とする.
[2]
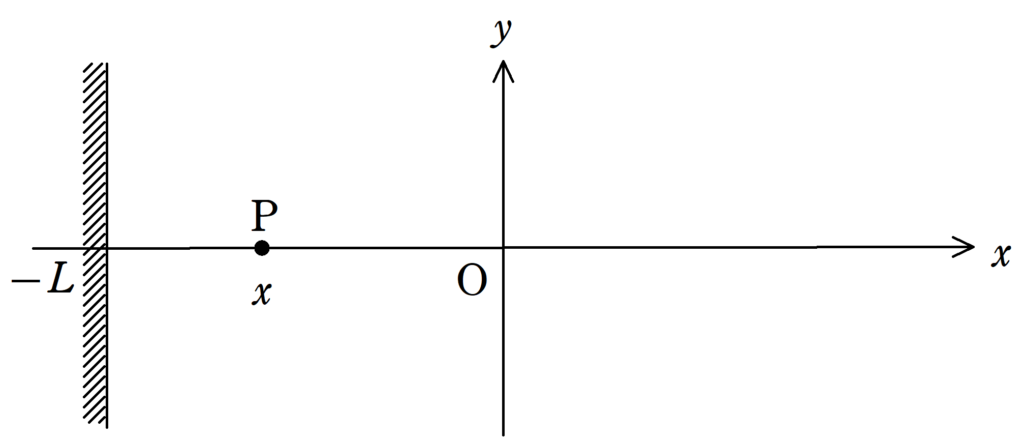
原点Oの時刻$t$における媒質の変位$y_{\rm{O}}(t)$が振幅$A$,周期$T$として
$y_{\rm{O}}(t)=A\sin\dfrac{2\pi}{T}t$
であった.この媒質の振動が速さ$v$で$x$軸の負の方向に伝わっている.
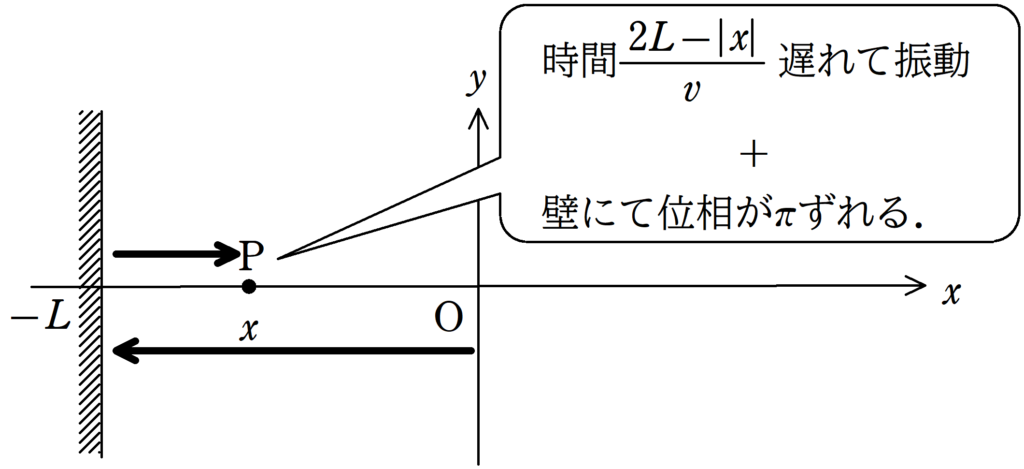
この波が媒質Pに直接伝わる入射波とPを通りすぎ,$x=-L$において反射して再びPに伝わる反射波について次の問いに答えよ.
(1) 座標$x(x<0)$にある媒質Pに直接伝わる入射波の時刻$t$における波の変位$y_{\rm{P1}}(t)$の時間変化を求めよ.
(2) 座標$x(x<0)$にある媒質Pを通りすぎて$x=-L$にある壁で反射された波が再びPにたどりついた.このとき,時刻$t$における媒質Pの反射波の変位$y_{\rm{P2}}(t)$の時間変化を求めよ.ただし,壁での反射は自由端反射とする.
(3) 座標$x(x<0)$にある媒質Pを通りすぎて$x=-L$にある壁で反射された波が再びPにたどりついた.このとき,時刻$t$における媒質Pの反射波の変位$y_{\rm{P3}}(t)$の時間変化を求めよ.ただし,壁での反射は固定端反射とする.
<解答>
[1]
(1) OP間の距離は$x$なので,Oの振動がPに伝わる時間は$\dfrac{x}{v}$です.
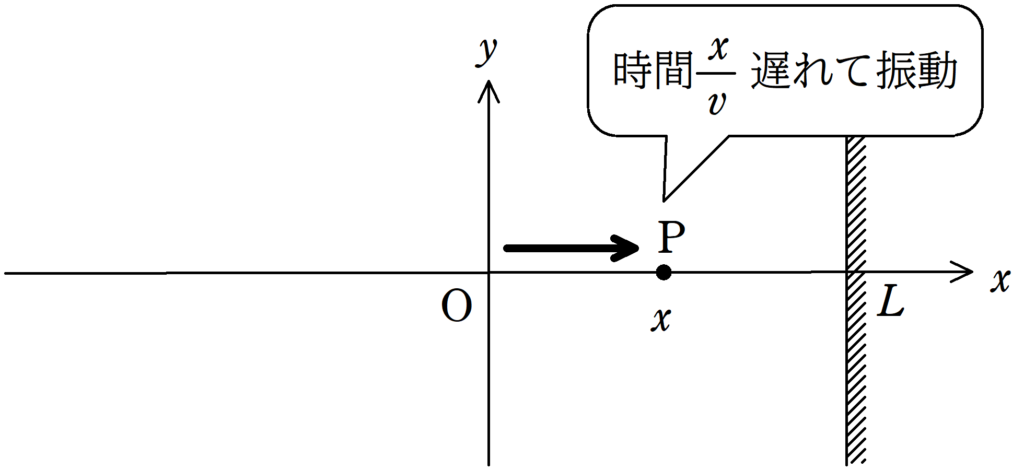
$y_{\rm{P1}}(t)=A\cos\dfrac{2\pi}{T}\left(t-\dfrac{x}{v}\right)$
(2) O→壁→Pの距離は$2L-x$なので,Oの振動がP(反射波)に伝わる時間は$\dfrac{2L-x}{v}$です.
また,壁では自由端反射するので,反射による位相のずれはありません.
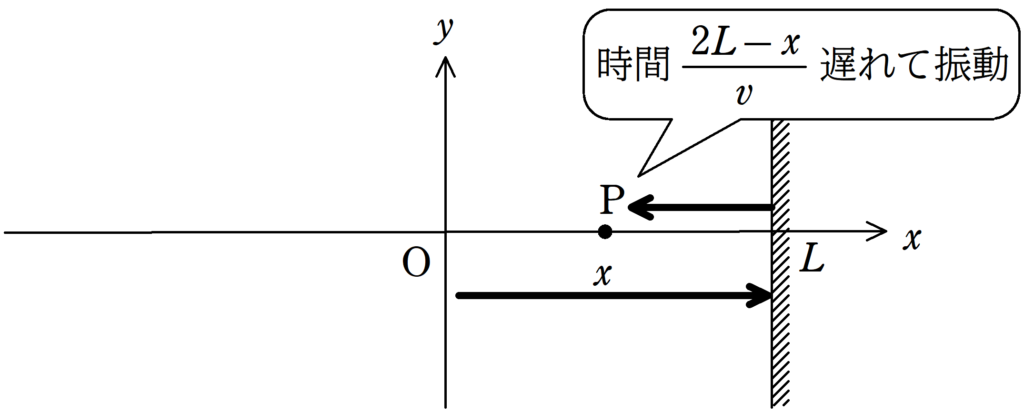
$y_{\rm{P2}}(t)=A\cos\dfrac{2\pi}{T}\left(t-\dfrac{2L-x}{v}\right)$
(3) O→壁→Pの距離は$2L-x$なので,Oの振動がP(反射波)に伝わる時間は$\dfrac{2L-x}{v}$です.
また,壁では固定端反射するので,反射による位相のずれは$\pi$です.
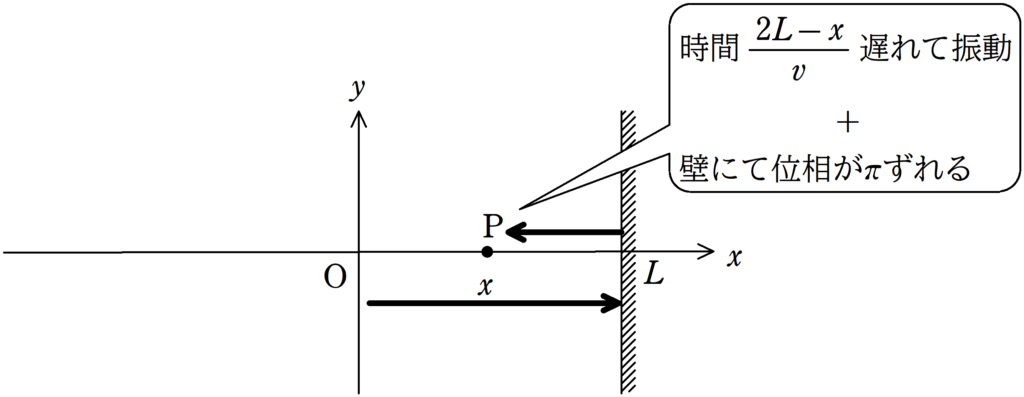
$y_{\rm{P3}}(t)=A\cos\left\{\dfrac{2\pi}{T}\left(t-\dfrac{2L-x}{v}\right)+\pi\right\}=-A\cos\dfrac{2\pi}{T}\left(t-\dfrac{2L-x}{v}\right)$
[2]
(1) OP間の距離は$x$ではなく,$|x|$です!$x<0$なので,$|x|=-x$ですね.
したがって,OからPに振動が伝わる時間は$\dfrac{|x|}{v}=\dfrac{-x}{v}$となります.
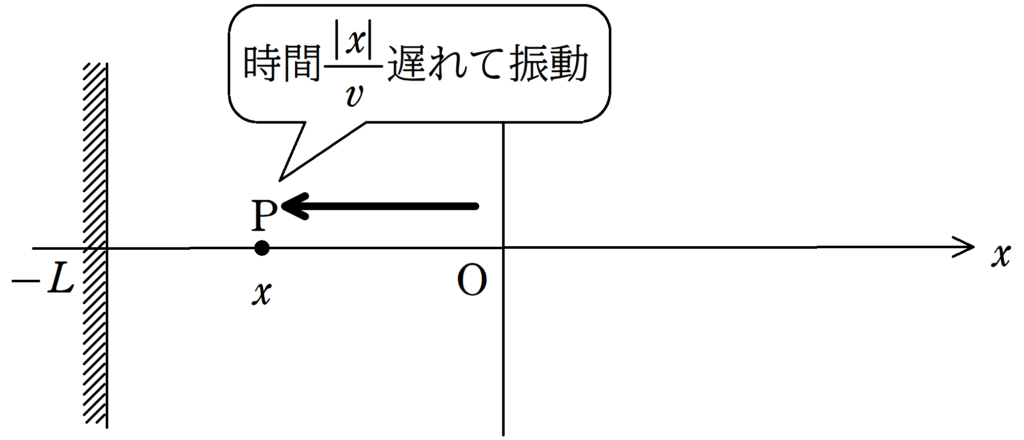
$y_{\rm{P1}}(t)=A\sin\dfrac{2\pi}{T}\left(t-\dfrac{-x}{v}\right)=A\sin\dfrac{2\pi}{T}\left(t+\dfrac{x}{v}\right)$
(2) O→壁→Pの距離は$2L-|x|=2L+x$なので,Oの振動がP(反射波)に伝わる時間は$\dfrac{2L+x}{v}$です.
また,壁では自由端反射するので,反射による位相のずれはありません.
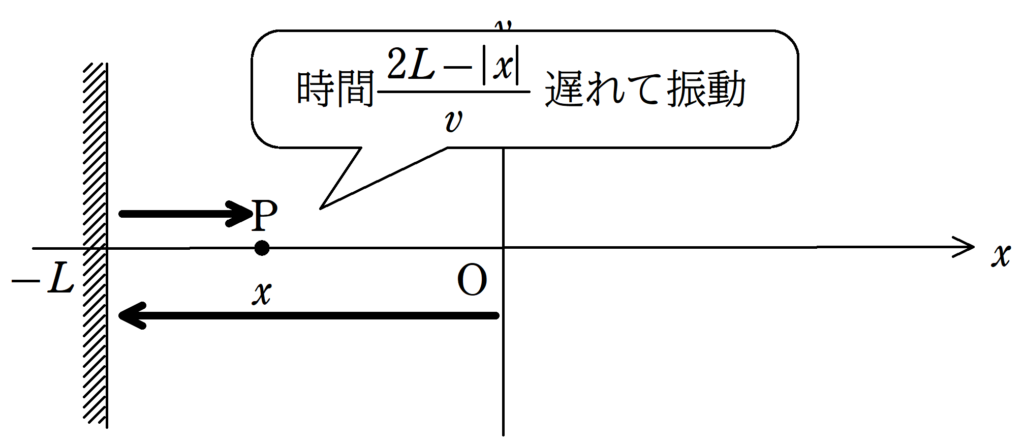
$y_{\rm{P2}}(t)=A\sin\dfrac{2\pi}{T}\left(t-\dfrac{2L+x}{v}\right)$
(3) O→壁→Pの距離は$2L-|x|=2L+x$なので,Oの振動がP(反射波)に伝わる時間は$\dfrac{2L+x}{v}$です.
また,壁では固定端反射するので,反射による位相のずれは$\pi$です.
$y_{\rm{P3}}(t)=A\sin\left\{\dfrac{2\pi}{T}\left(t-\dfrac{2L+x}{v}\right)+\pi\right\}=-A\sin\dfrac{2\pi}{T}\left(t-\dfrac{2L+x}{v}\right)$

ポイントは
- どのくらい遅れて伝わるのか.
- 途中で反射による位相のずれはあるのか.
だね.



コメント
[…] {2pi (dfrac{t}{T}-dfrac{x}{lambda})}$ $dots (ast)$…physicmath.net2020.08.23 [演習問題]波の式を立てる.$y(0 ,t)$から$y(x , t)$の式へNEKO下の記事にある波… […]
[…] [演習問題]波の式を立てる.$y(0 ,t)$から$y(x , t)$の式へNEKO下の記事にある波… […]
[…] “[演習問題]波の式を立てる.$y(0 ,t)$から$y(x , t)$の式へ” […]
[…] 分野別 Twitter Facebook はてブ LINE 2021/3/2 NEKO [演習問題]波の式を立てる.$y(0 ,t)$から$y(x , t)$の式へNEKO下の記事にある波… […]
[…] [演習問題]波の式を立てる.$y(0 ,t)$から$y(x , t)$の式へNEKO下の記事にある波… […]
[…] [演習問題]波の式を立てる.$y(0 ,t)$から$y(x , t)$の式へNEKO下の記事にある波… […]
[…] [演習問題]波の式を立てる.$y(0 ,t)$から$y(x , t)$の式へNEKO下の記事にある波… […]
[…] [演習問題]波の式を立てる.$y(0 ,t)$から$y(x , t)$の式へNEKO下の記事にある波… […]