
今回は定常波の式を扱います.
波の式に詳しく知りたい方は,こちらを参考にしてください.

それでは,さっそく問題を解いてみましょう.
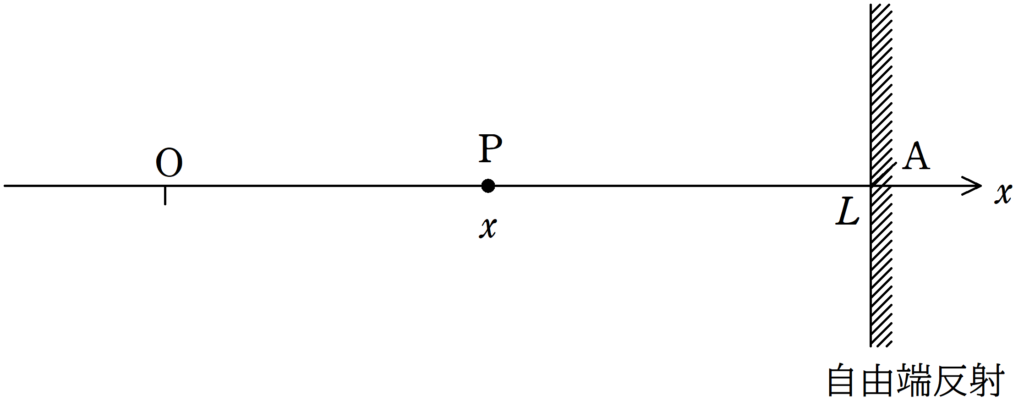
原点Oにある媒質の変位$y_{\rm O}$は振幅$A$,周期$T$,時刻$t$を用いて次のように表される.
$y_{\rm O}=A\sin\dfrac{2\pi}{T}t$
このとき,$x$軸上を速さ$v$で伝わる波を考える.
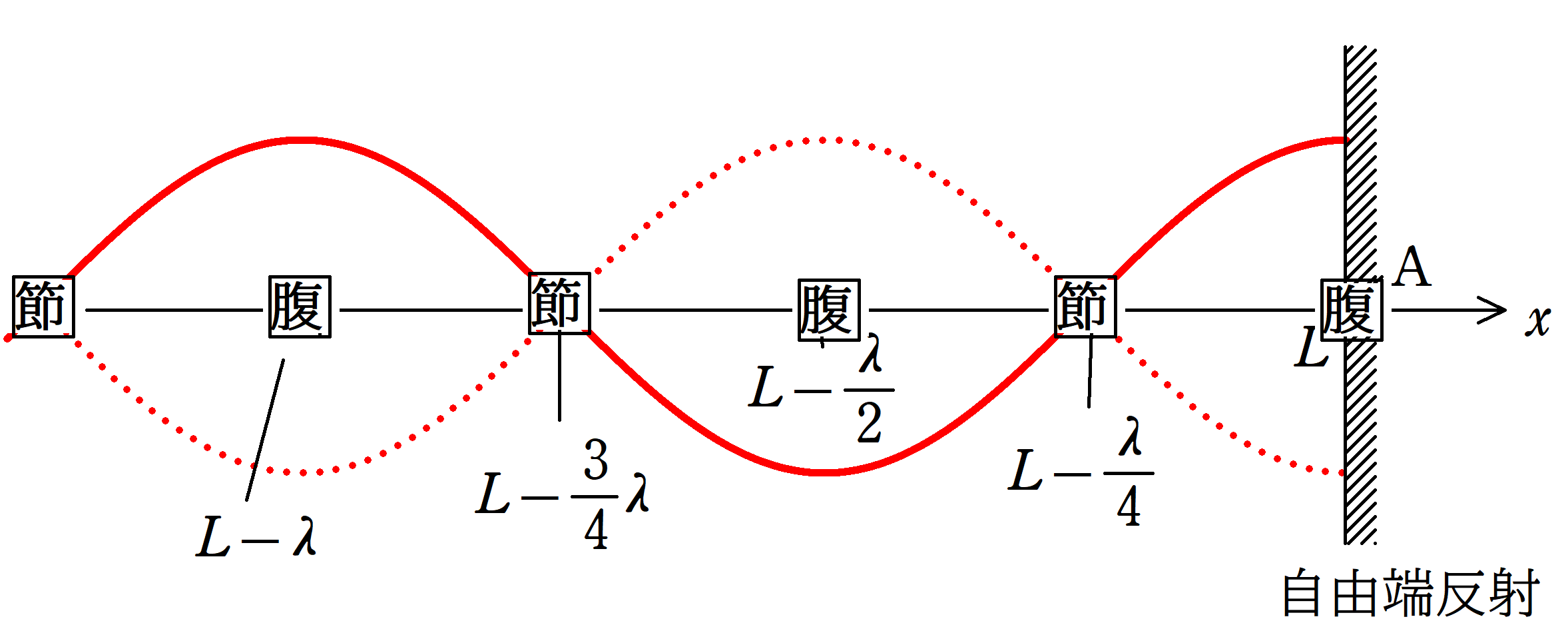
$x=L(L>0)$には壁があり,この壁では自由端反射をするものとする.
原点Oから出発し,直接P(座標$x$)にたどり着く入射波と原点Oから出発し,壁に反射してからPにたどり着く反射波を重ね合わせの原理によって合成することで,Pでの波の式を求めよ.
<解答>

Pにおける入射波の変位を$y_{1}$,反射波の変位を$y_{2}$としましょう.
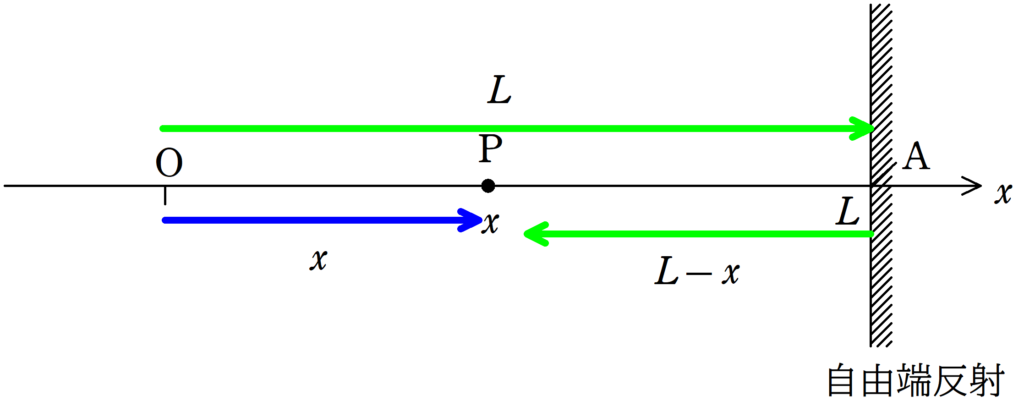

波は振動が遅れて伝わる現象だったね.
OからPまでは時間$\dfrac{x}{v}$だけかかるから,Pにおける入射波の媒質の変位は,時間$\dfrac{x}{v}$前の原点Oにおける媒質の変位と等しいんだね.
$y_{1}=A\sin\dfrac{2\pi}{T}(t-\dfrac{x}{v})$ $\dots (\ast)$

また,Oから反射点Aを経由してPまでの距離は
$L+(L-x)=2L-x$
なので,O→A→Pまでは
$\dfrac{2L-x}{v}$
の時間がかかるね.
このことから,Pにおける反射波の変位は,時間$\dfrac{2L-x}{v}$前のOでの変位と等しいので,$y_{2}$は次のようになります.
$y_{2}=A\sin\dfrac{2\pi}{T}(t-\dfrac{2L-x}{v})$ $\dots (2\ast)$

$y_{1}+y_{2}$がPの媒質の合成波の変位です.
重ね合わせの原理ですね.
2つ以上の波がある場合,その合成波は媒質の変位の足し算となる.
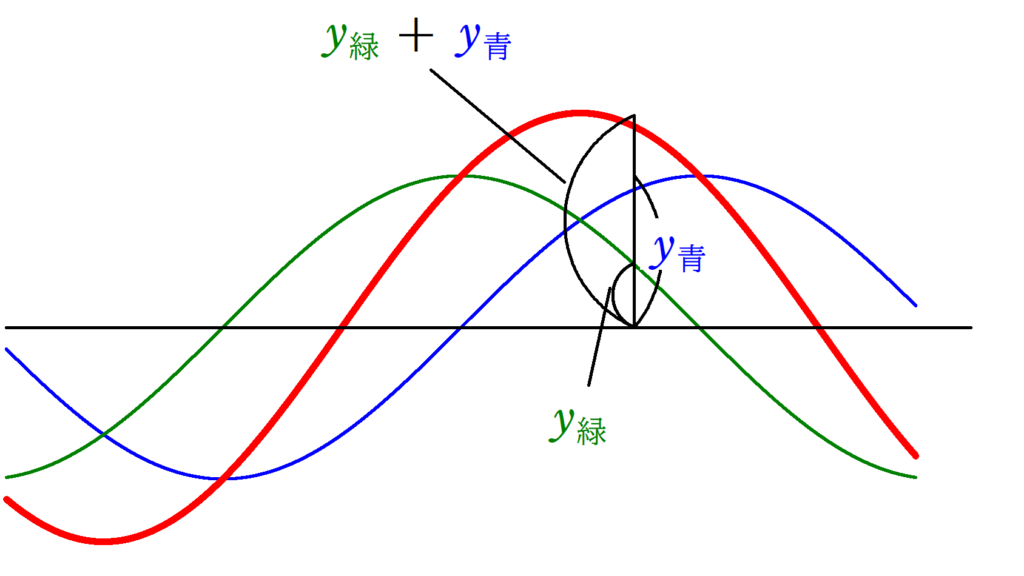
たとえば,青の波と緑の波がある場合,青の波の変位を$y_{青}$,緑の波の変位を$y_{緑}$とすれば,合成波(赤色の波)の変位は,
$y_{合成波}$$=$$y_{青}$$+$$y_{緑}$

ところが,そのままの形では,Pにある媒質がどのように振動するかがわかりにくため,三角関数の和→積の変換式を使います.

三角関数の和→積の変換式(その逆の積→和も同様)は,覚えるのが大変なので,導出方法を知っておくとよいでしょう.
★ $\sin +\sin$について
1. $\sin$の加法定理を書き出す.
$\sin(\alpha +\beta)=\sin\alpha\cos\beta +\cos\alpha\sin\beta$ $\dots (\ast)$
$\sin(\alpha -\beta)=\sin\alpha\cos\beta -\cos\alpha\sin\beta$ $\dots (2\ast)$
2. $(\ast)+(2\ast)$を計算する.
$\sin(\alpha +\beta)+\sin(\alpha -\beta)=2\sin\alpha\cos\beta$ $\dots (3\ast)$
3. $A=\alpha +\beta$,$B=\alpha -\beta$とする.
$A+B=2\alpha$ $\therefore \alpha=\dfrac{A+B}{2}$ $\dots (\clubsuit)$
$A-B=2\beta$ $\therefore \beta=\dfrac{A-B}{2}$ $\dots (\spadesuit)$
4. $(\clubsuit),(\spadesuit)$を$(3\ast)$に代入
$\sin A+\sin B=2\sin\dfrac{A+B}{2}\cos\dfrac{A-B}{2}$
★ $\cos -\cos$について
1. $\cos$の加法定理を書き出す.
$\cos(\alpha +\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta$ $\dots (\ast)$
$\cos(\alpha -\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta$ $\dots (2\ast)$
2. $(\ast)+(2\ast)$を計算する.
$\cos(\alpha +\beta)+\cos(\alpha -\beta)=2\cos\alpha\cos\beta$ $\dots (3\ast)$
3. $A=\alpha +\beta$,$B=\alpha -\beta$
$A+B=2\alpha$ $\therefore \alpha=\dfrac{A+B}{2}$ $\dots (\clubsuit)$
$A-B=2\beta$ $\therefore \beta=\dfrac{A-B}{2}$ $\dots (\spadesuit)$
4. $(\clubsuit),(\spadesuit)$を$(3\ast)$に代入
$\cos A+\cos B=2\cos\dfrac{A+B}{2}\cos\dfrac{A-B}{2}$

三角関数の和→積の変換式を使えば,$y_{1}+y_{2}$は次のようになるね.
$y_{1}=A\sin\dfrac{2\pi}{T}(t-\dfrac{x}{v})$,$y_{2}=A\sin\dfrac{2\pi}{T}(t-\dfrac{2L-x}{v})$より
$\eqalign{y_{1}+y_{2}&=2A\sin\dfrac{1}{2}\{\dfrac{2\pi}{T}(t-\dfrac{x}{v})+\dfrac{2\pi}{T}(t-\dfrac{2L-x}{v})\}\cos\dfrac{1}{2}\{\dfrac{2\pi}{T}(t-\dfrac{x}{v})-\dfrac{2\pi}{T}(t-\dfrac{2L-x}{v})\}\\&=2A\sin\dfrac{2\pi}{T}(t-\dfrac{L}{v})\cos\dfrac{2\pi}{T}\cdot\dfrac{L-x}{v}}$

また,波の基本式を使い,$Tv=\lambda$として,並び替えてみましょう.
$y_{1}+y_{2}=$$2A\cos\dfrac{2\pi}{\lambda}(L-x)$$\sin\dfrac{2\pi}{T}(t-\dfrac{L}{v})$ $\dots (\heartsuit)$ (答)

$(\heartsuit)$式の赤い部分は時刻$t$によって変化する部分です.
赤い部分を振動部分と呼びましょう.
一方,青い部分は時刻$t$にはよりません.
つまり,$|2A\cos\dfrac{2\pi}{\lambda}(L-x)|$が振幅です.
この式をみると,振幅は$x$によって変化することがわかります.
振幅が最大になる場所と最小となる場所を探してみましょう.
★ 振幅が最大になる場所
$|2A\cos\dfrac{2\pi}{\lambda}(L-x)|$について,$\cos\dfrac{2\pi}{\lambda}(L-x)=\pm 1$のとき,最大となるので,$m$を整数として
$\dfrac{2\pi}{\lambda}(L-x)=\pi m$
$x=L-\dfrac{m}{2}\lambda$
具体的には,
$x=L , L-\dfrac{\lambda}{2} , L-\lambda, \dots$

このように,振幅が最大となるところを腹(はら)
といいます.
★ 振幅が最小になる場所
$|2A\cos\dfrac{2\pi}{\lambda}(L-x)|$について,$\cos\dfrac{2\pi}{\lambda}(L-x)=0$のとき,最小となるので,$m$を整数として
$\dfrac{2\pi}{\lambda}(L-x)=\dfrac{2m-1}{2}\pi$
$x=L-\dfrac{2m-1}{4}\lambda$
具体的には
$x=L-\dfrac{1}{4}\lambda , L-\dfrac{3}{4}\lambda , \dots$

このように,振幅が0,すなわち,いつまでも振動しないところを節(ふし)といいます.

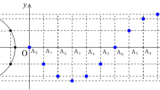
いままでのことを総合すると,それぞれの媒質の振幅は次のように表すことができるんだね.
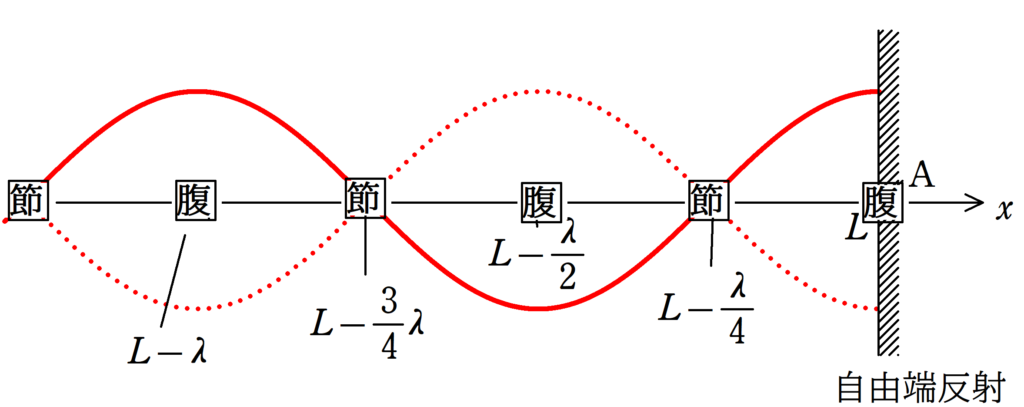

このように,波長,振幅,速さが同じで逆方向に進む波が干渉することでできる合成波は,進行しているようには見えずただ振動しているように見えます.
このような波を定常波と言います.
定常波は,最も大きく振動する腹と,一切振動しない節の部分があり,隣り合う腹と節の距離は$\dfrac{1}{4}\lambda$となります.



コメント