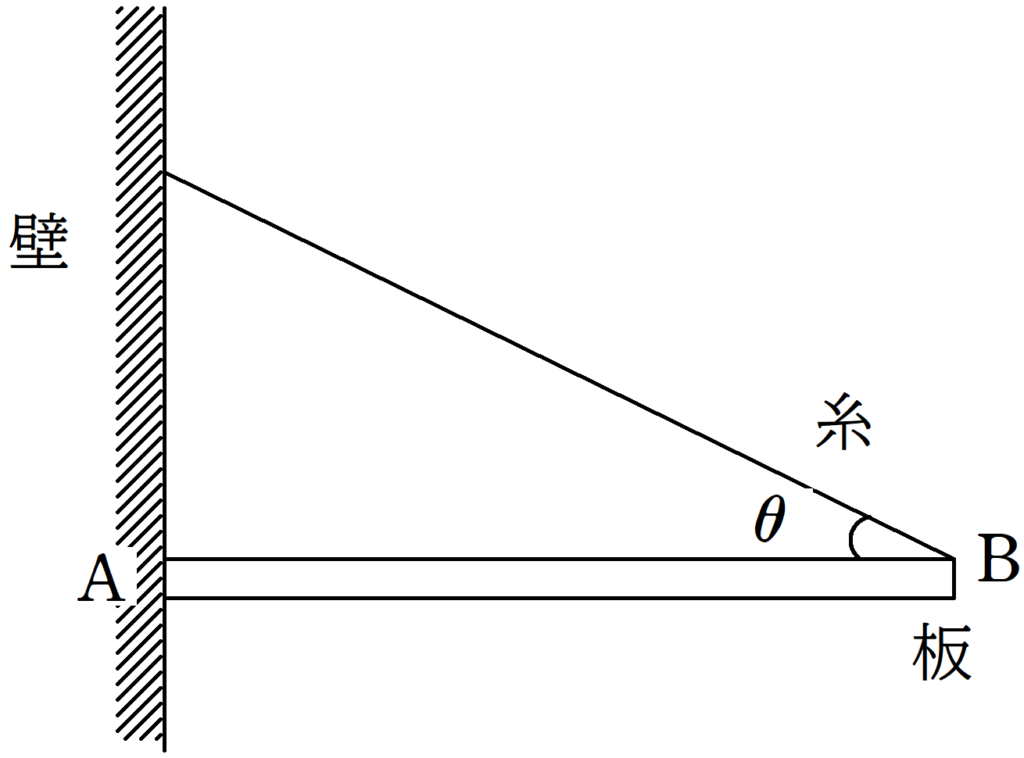
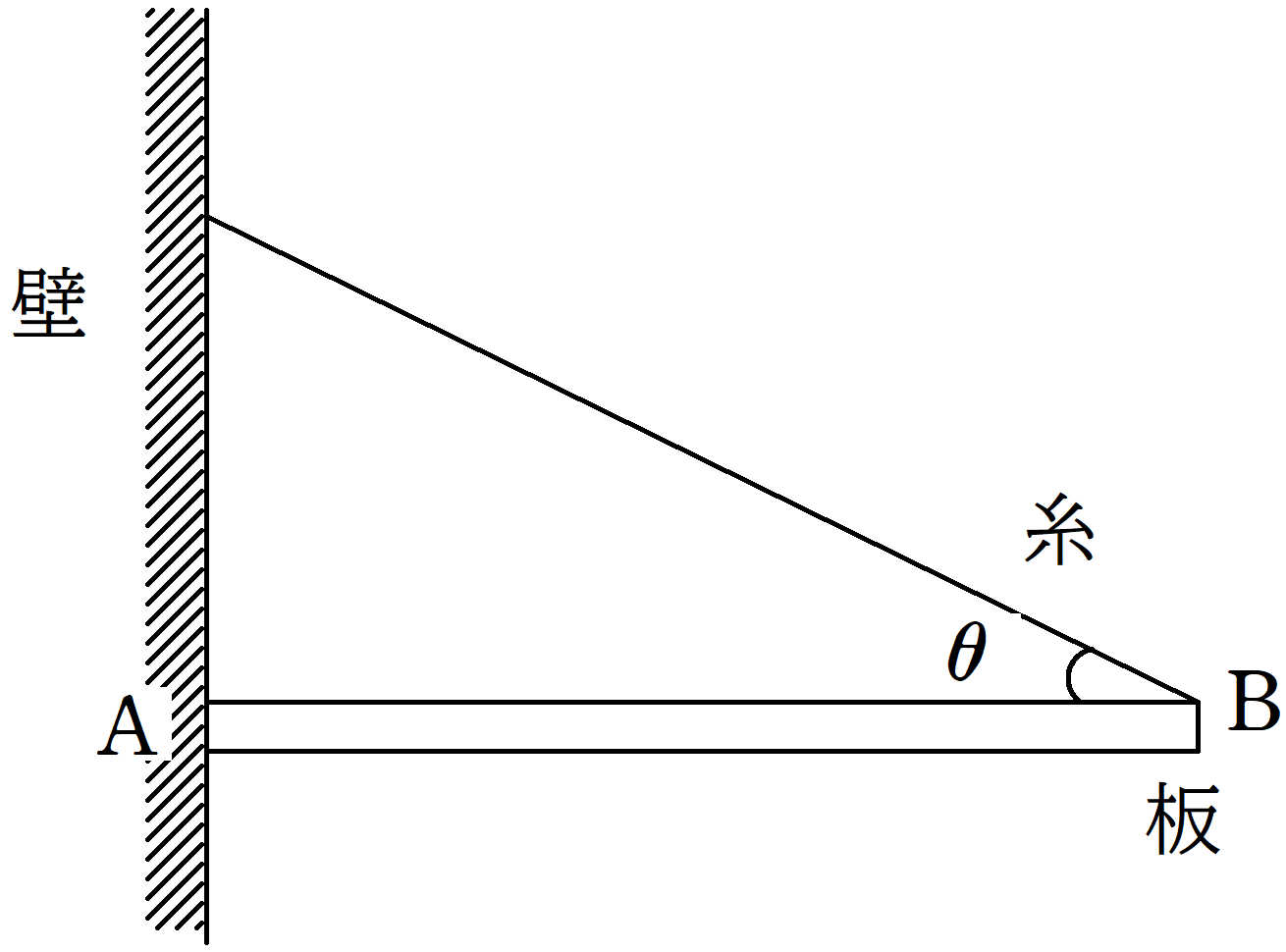
質量$m$で長さ$l$の密度が一様でまっすぐな板の端$\rm A$をあらい鉛直な壁に接触させ,端$\rm B$には軽くて伸びない糸を取りつける.糸と板の長さ方向のなす角は$\theta(0<\theta<\dfrac{\pi}{2})$である.重力加速度の大きさを$g$として,次の問いに答えよ.
(1) $\rm B$にはたらく張力の大きさを$T$,$\rm A$にはたらく垂直抗力の大きさを$N$,摩擦力の大きさを$f$とする.板に関する水平方向と鉛直方向のつり合いの式を立てよ.
(2) $\rm A$まわりの力のモーメントのつり合いの式を立てよ.
(3) (1),(2)より$T$,$N$,$f$を$m$,$g$,$\theta$から必要なものを用いて表せ.
<解答>
(1)
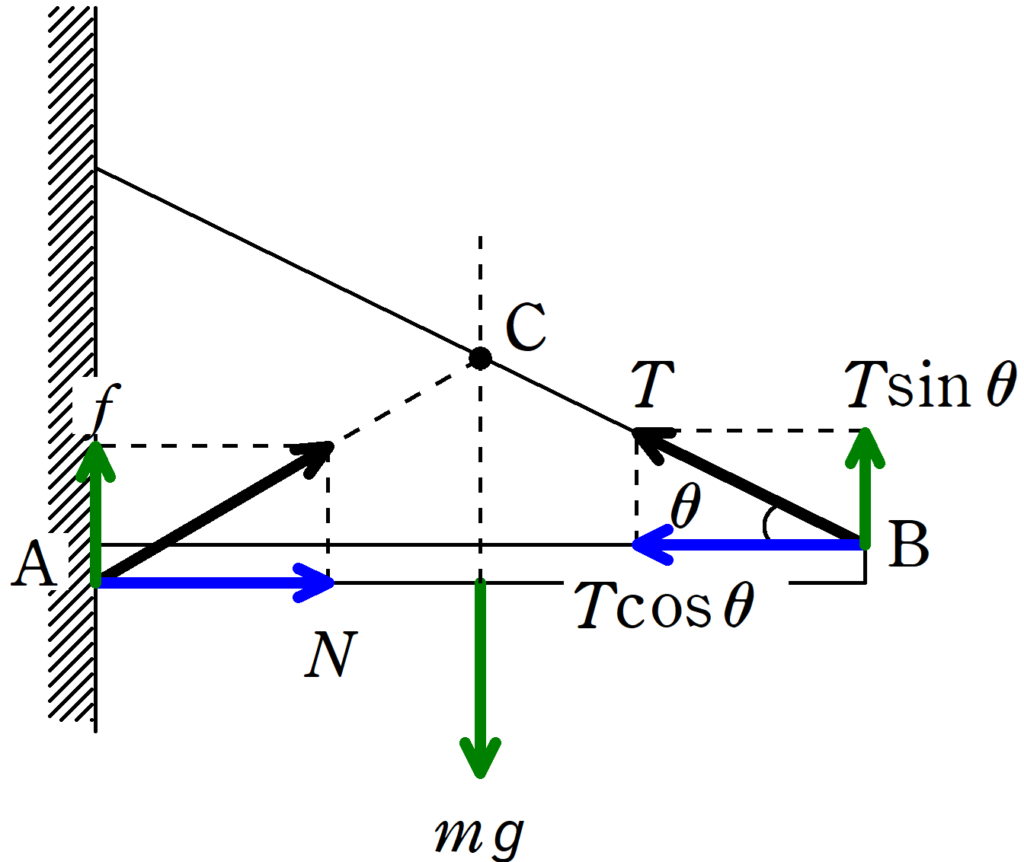

板にはたらく水平方向の力は青色で,鉛直方向の力は緑で図示しました.
張力$T$は水平方向と鉛直方向に分解しています.
★ 水平方向のつり合いの式
$N=T\cos\theta$ $\dots (\ast)$ (答)
★ 鉛直方向のつり合いの式
$f+T\sin\theta=mg$ $\dots (2\ast)$ (答)
(2)
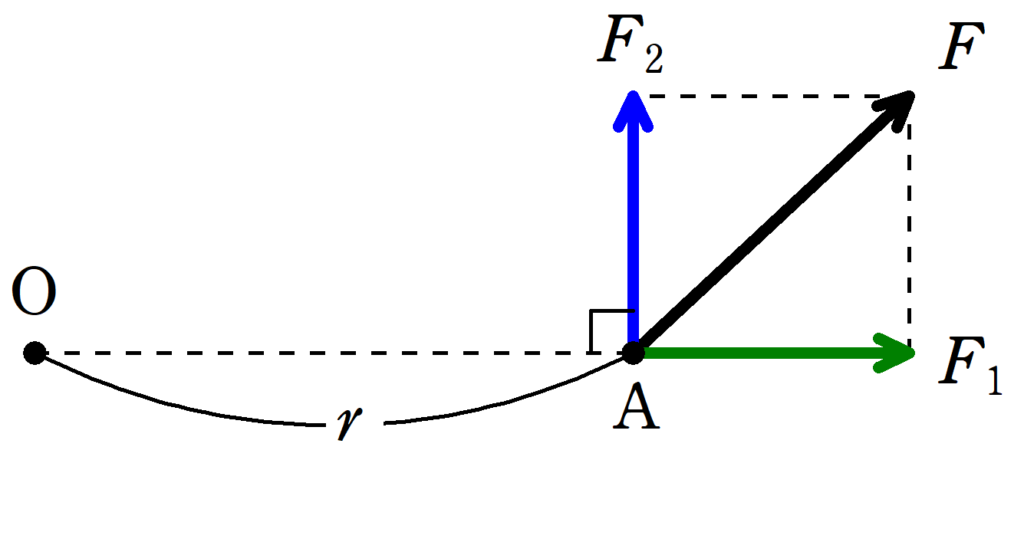
中心$\rm O$から距離$r$の点$\rm A$を始点とした大きさ$F$の力がはたらいている.この力の$\rm OA$方向の成分を$F_{1}$,$\rm OA$に垂直な成分を$F_{2}$とすると,力$F$の点$\rm O$まわりの力のモーメントの大きさ$N$は
$N=rF_{2}$
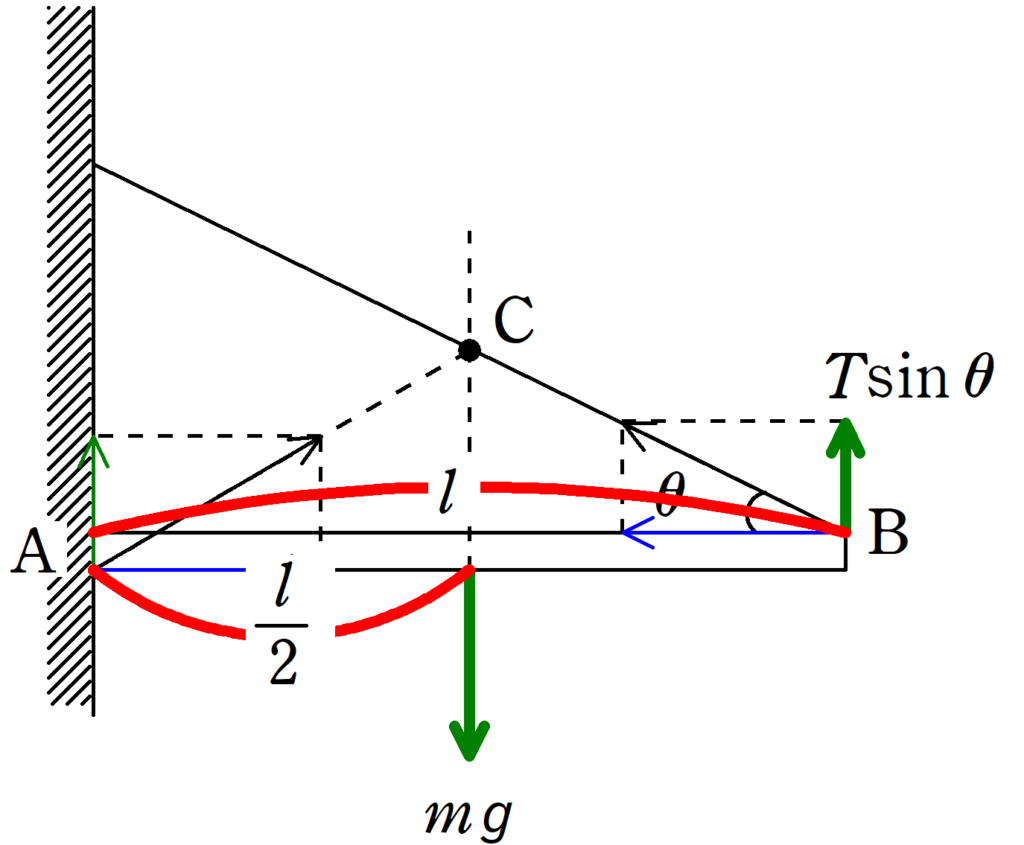

Aまわりのモーメントのつり合いの式を立てます.
Aから重力の作用線までの距離は$\dfrac{l}{2}$,AからBまでの距離が$l$です.
★ 力のモーメントのつり合いの式
$\dfrac{l}{2}\cdot mg=l\cdot T\sin\theta$ (答)
(3) (2)より,
$\therefore T=\dfrac{mg}{2\sin\theta}$ $\dots (3\ast)$ (答)
$(3\ast)$と$(\ast)$より
$\eqalign{N&=T\cos\theta\\&=\dfrac{mg}{2\sin\theta}\cdot \cos\theta \\&=\dfrac{mg}{2\tan\theta}}$ (答)
$(3\ast)$と$(2\ast)$より
$\eqalign{f+T\sin\theta&=mg\cr f&=mg-\dfrac{mg}{2\sin\theta}\cdot \sin\theta \\&=\dfrac{mg}{2}}$ (答)


コメント
[…] […]