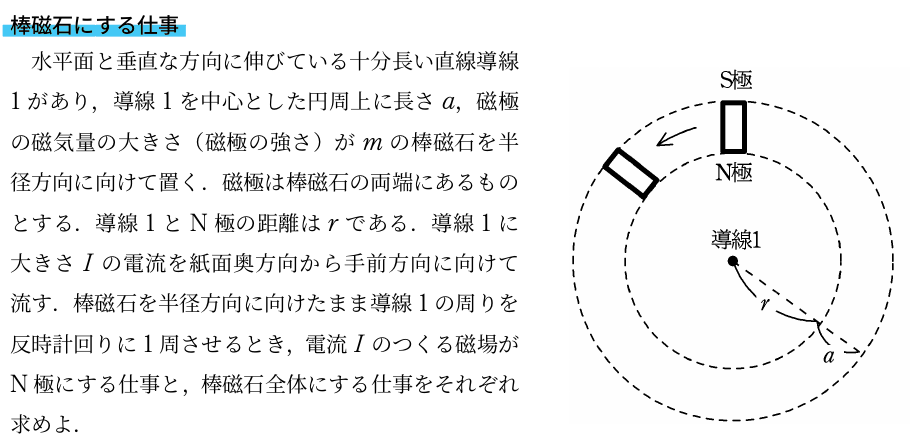
<問題>
<解答>
十分長い直線電流がつくる磁場は次のようになります.
十分長い直線電流が距離$r$の位置につくる磁場$H_{1}$は,導線に流れる電流の大きさを$I_{1}$とすると
$H_{1}=\dfrac{I_{1}}{2\pi r}$
向きは右ねじの法則にしたがいます.
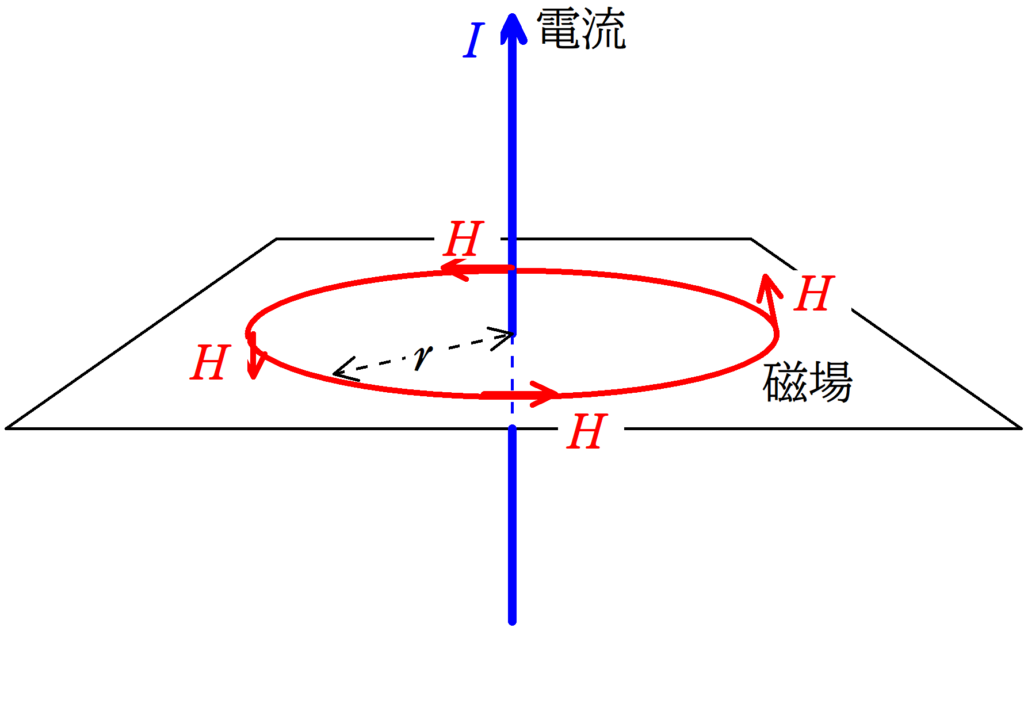
※ 右ねじの法則は右手の親指→電流,4本指→磁場 です.
また,磁場中に磁荷がある場合に受ける力は次のようになります.
大きさ$H$の磁場中に磁気量の大きさ$m$の物体があるとき,物体が受ける力の大きさ$F$は
$F=mH$
$m>0$(N極側)のときは,磁場と同じ方向に力を受け,$m<0$(S極側)のときは,磁場と反対方向に力を受ける.
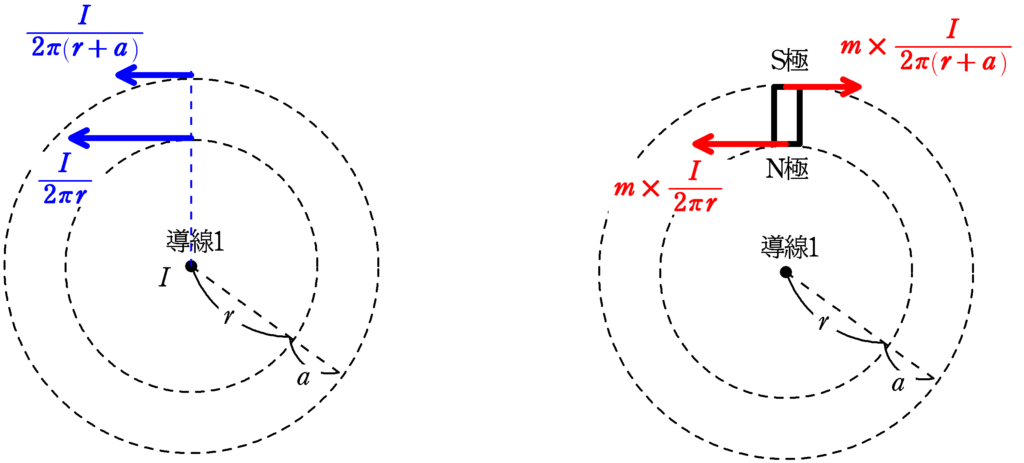
導線1が半径$r$の円周上につくる磁場の大きさは$\dfrac{I}{2\pi r}$,半径$r+a$の円周上につくる磁場の大きさは$\dfrac{I}{2\pi (r+a)}$で,磁場の向きは上図左のようになります.(右ねじの法則)
すると,N極は磁場と同じ方向に力を受け,その大きさ$F_{\rm N}$は
$F_{\rm N}=m\times \dfrac{I}{2\pi r}$
となります.また,S極は磁場と反対方向に力を受け,その大きさ$F_{\rm S}$は
$F_{\rm S}=m\times \dfrac{I}{2\pi (r+a)}$
N極は1周$2\pi r$を動くので,磁場がN極にする仕事$W_{\rm N}$は
$W_{\rm N}=F_{\rm N}\times 2\pi r=mI$ (答)
また,S極は1周$2\pi(r+a)$を動くので,磁場がS極にする仕事$W_{\rm N}$は(力と動く方が逆であることから負の仕事であることに注意して)
$W_{\rm S}=-F_{\rm S}\times 2\pi(r+a)=-mI$
したがって,磁場が棒磁石全体にする仕事$W$は
$W=W_{\rm N}+W_{\rm S}=mI-mI=0$ (答)


コメント