高校物理であとまわしにしがちな原子物理の単元.触れる機会も少ないので,知識もあいまいになりがちです.そこで,今回は光電効果について知識を整理しましょう.この記事を読んで入試の基礎をおさえておきましょう.
光電効果とは
金属に光を当てると電子が飛び出る現象を光電効果といいます.飛び出た電子を光電子といいます.光電効果は光の粒子性を説明する現象として有名です.
光子のエネルギー
光子とは,光を粒子とみたときの呼び名です.光電効果は光を粒子と見た方が説明がうまくいきます.この1個あたりの光子のエネルギーは振動数$\nu$に比例します.そもそも光の正体は電磁波であり,おおまかにその波長によって分類しています.
電磁波の波長の大きさは
電波>赤外線>可視光線>紫外線>$X$線>$\gamma$線
光の速さを$c$,波長を$\lambda$,振動数を$\nu$とすると,波の基本式から
$c=\nu \lambda$ $\therefore \nu =\dfrac{c}{ \lambda}$
であるから,振動数は波長に反比例します.つまり,振動数の大きさは
電波<赤外線<可視光線<紫外線<$X$線<$\gamma$線
振動数が大きいものはエネルギーが大きいので,たとえば,赤外線と紫外線では紫外線の方がエネルギーが高いことになります.イメージわきますか?
話をもどします.光子1個のエネルギーは振動数$\nu$に比例します.その比例定数をプランク定数$h$とすると,光子1個あたりのエネルギー$E$は
$E=h \nu$
です.プランク定数hは$6.63×10^{-34}\rm{Js}$という非常に小さい値をとります.
光子が$N$個の場合は総エネルギーは$Nh\nu$となります.また,単位時間当たりに受ける光のエネルギー量を光の強さとし,光の強さ$L$は単位時間,単位面積あたりにあたる光子の個数$n$を用いて
$L=nh\nu$
光電効果の式
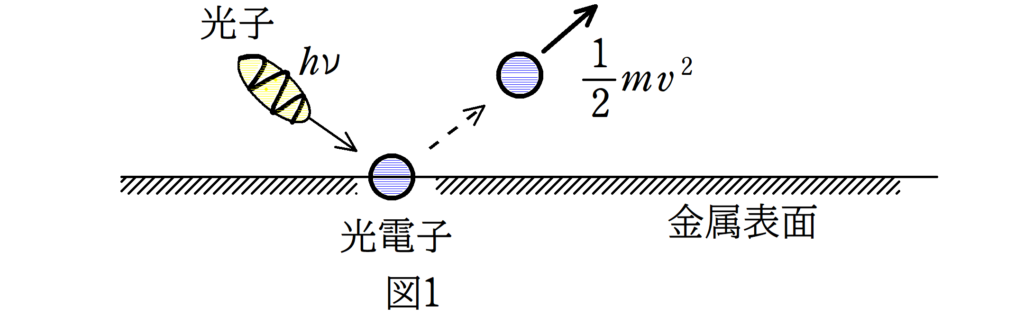
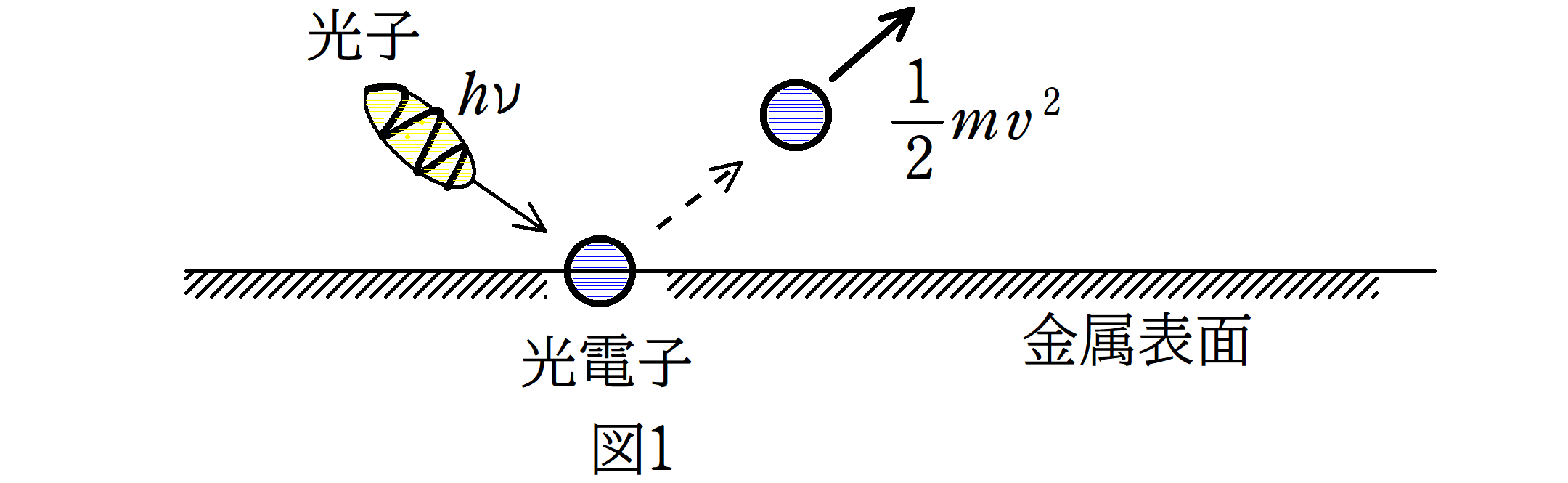
図1は光電効果のイメージ図です.光子1個が光電子にあたり,光子のエネルギーをもらった光電子が金属の束縛から逃れて飛び出します.しかし,いつでも光電子が飛び出せるわけではありません.
たとえば,金属表面から抜け出すのに必要なエネルギーが100だとします.しかし,光子のエネルギーが50では,そのエネルギーをもらった電子は飛び出すことができません.
金属表面から飛び出すのに必要なエネルギーを仕事関数といい,$W$で表しましょう.電子が飛び出すには
$W \leq h \nu $
を満たすときです.
$W= h\nu_{0}$ $\therefore$ $\nu_{0}=\dfrac{W}{h}$
のように,ギリギリ光電子が飛び出すのに必要な光子の振動数$\nu_{0}$を限界振動数といいます.
限界振動数を超える振動数の光を金属にあてると,光電子は金属表面から飛び出します.しかし,光子のエネルギーすべてを光電子がもらえるわけではなく,一部金属表面から脱出するのにエネルギーが使われてしまうので,光電子の運動エネルギーは
$\dfrac{1}{2}mv^2=h\nu -W$ ($\ast$)
これを光電効果の式といいます.この式はエネルギーの関係式なので,意味を考えて立式をしましょう.
光電子の運動エネルギーの測定
さて,飛び出した光電子の運動エネルギーはどのように測定すればよいのでしょうか.飛び出した光電子の速さを調べればいいじゃないかと思うかもしれませんが,ではどのように速さを調べればよいのでしょうか.目に見えない電子のスピードを直接的に測るのはかなり困難です.そこで,次のように工夫をして測定します.
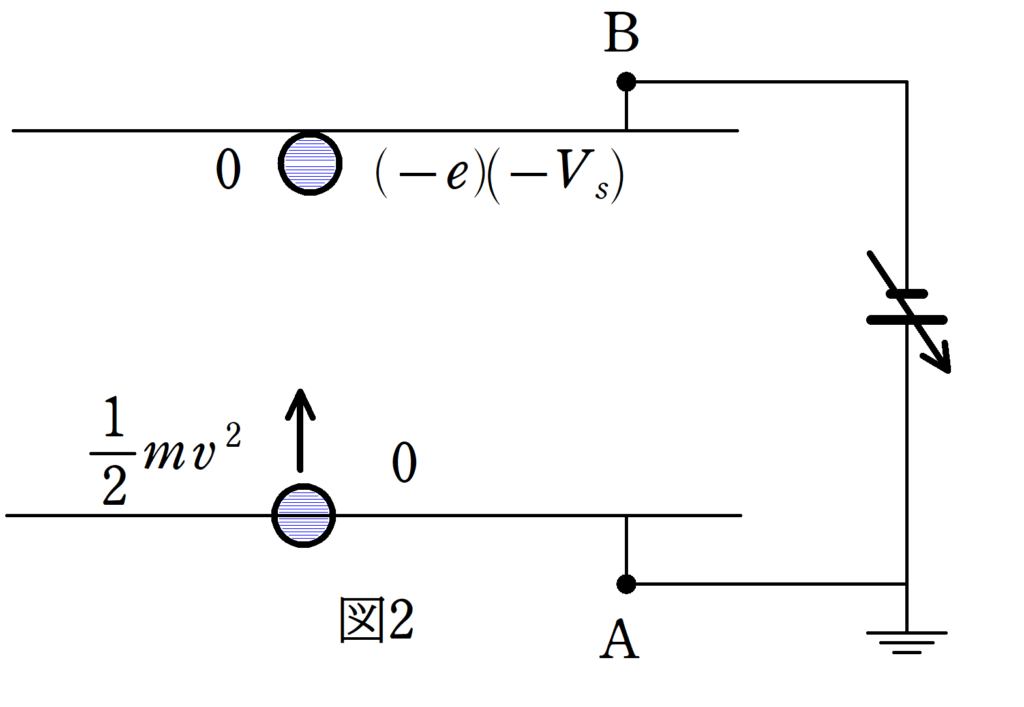
図2のような回路をつくり,飛び出した電子を減速させるように電圧をかけるのです.
あまりに,大きな電圧をかけすぎすると,大きなクーロン力がかかるため,光電子は反対方向にたどりつきません.しかし,電圧の大きさを小さくしていくとだんだんとクーロン力も弱くなり,ある電圧で光電子は反対方向に到着します.「到着する=電流が流れる」であるから,電流計を設置しておけば電子がたどりついたかがわかります.
この光電子が反対側にたどりつくときにかける電圧$V_{s}$を阻止電圧といいます.この阻止電圧を測定することで,光子の運動エネルギーを測定することができるのです.(大きな電圧から少しずつ電圧を小さくしていって,電流計の針が触れる瞬間の電圧が阻止電圧です.)
電子の電荷を$-e$,図2のAに対するBの電位を$-V_{s}$とすれば,力学的エネルギー保存則より
$\dfrac{1}{2}mv^2+(-e)・0=\dfrac{1}{2}m・0^2+(-e)(-V_{s})$
$\dfrac{1}{2}mv^2=eV_{s}$ ($2\ast$)
光電効果の式は($\ast$)だけで覚えるのはもったいなく,($2\ast$)も一緒に覚えておきましょう.
$eV_{s}=\dfrac{1}{2}mv^2=h\nu-W$
よく出るグラフ①(電流と電位の関係)
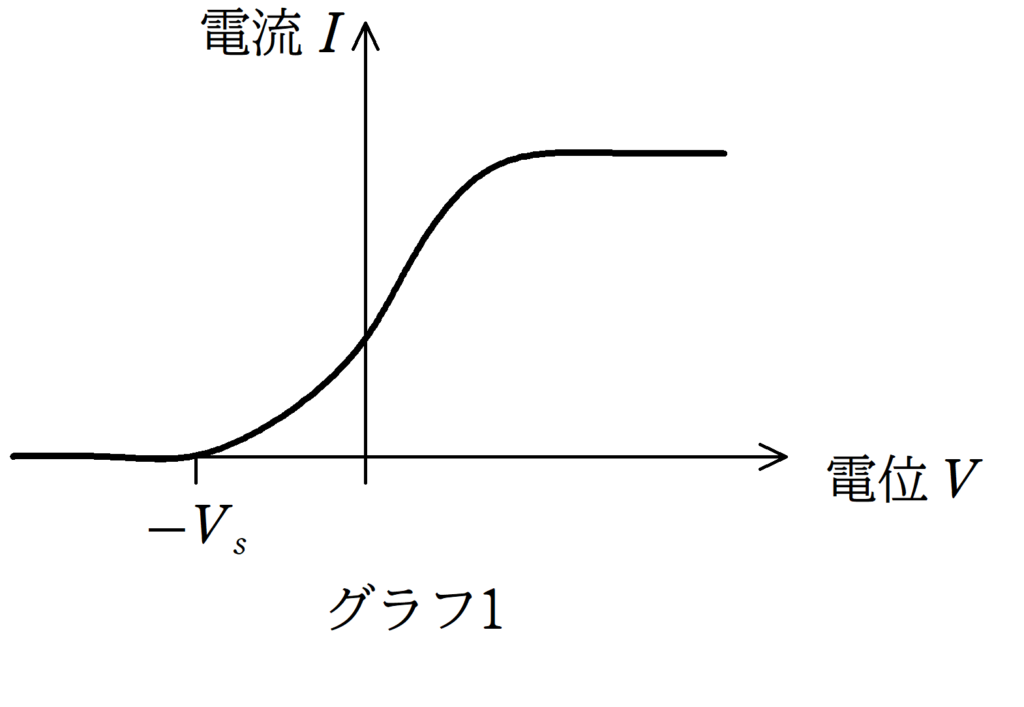
上のグラフ1は光電効果の問題でよく出るグラフの1つです.何を表しているグラフなのか確認しておきましょう.間違っても電流と電圧のグラフだからオームの法則かな?などとは思わないでください.電位というのは,図2におけるAに対するBの電位のことです.この電位が小さすぎると,AB間の電位差が大きいので,クーロン力が大きく,光電子はB側にたどりつきません.つまり,電子の移動がないので,電流は流れません.しかし,電位が$-V_s$になると,光電子がB側にたどり着き始めます.その結果電流が流れます.(一応確認ですが,電位が$-V_s$より小さくても光電子は飛び出しています.ただ,B側にたどり着かないだけです.もちろん,限界振動数以下では光電子は飛び出しませんが)すぐに電流が一定になっていないのは,飛び出てくる光電子に多少ばらつきがあるからと思ってください.最終的には電流は一定となります.電流は単位時間あたりに通過する電気量であるので,電流の大きさは単位時間当たりに飛び出る光電子の数に比例します.つまり,光の強さ(または明るさ)に比例することになります.
問題では,金属Aに当てる振動数や,光の明るさを変化させると,グラフ1がどのように変化していくかが問われることがあります.これはまた別な機会に考えていきましょう.
よく出るグラフ②(阻止電圧と振動数の関係)
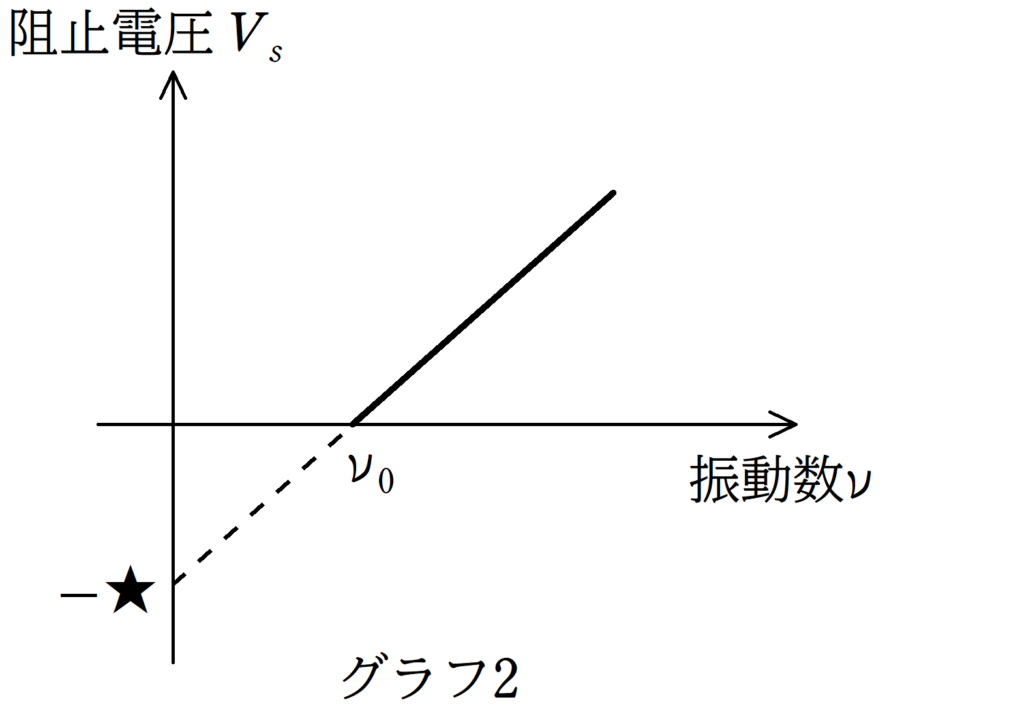
グラフ2は阻止電圧と振動数$\nu$の関係です.金属にあたえる振動数と阻止電圧の関係をグラフにプロットしていくと,上のようになりました.光電効果の式をみると
$eV_{s}=\dfrac{1}{2}mv^2=h\nu-W$
$V_{s}$$=\dfrac{h}{e}$$\nu$$-\dfrac{W}{e}$
これは
$y$$=a$$x$$+b$
との対応関係を考えればグラフ2の傾きは$\dfrac{h}{e}$,切片の絶対値が$\dfrac{W}{e}$となり,プランク定数や仕事関数の計算ができます.また,$\nu_0$は阻止電圧を0としたときの振動数であり,限界振動数に対応します.
注意してほしいのが,入試問題では縦軸が阻止電圧とは限らないということです.その都度,意味を考えて立式しましょう.
まとめ
★ 光子のエネルギー
$h$:プランク定数,$\nu$:光の振動数,$n$:単位時間当たりに面にあたる光子の数
光子1個あたりのエネルギー $E=h\nu$
光の強さ $L=nh\nu$
★ 光電効果の式
$-e$:電子の電荷,$m$:電子の質量,$v$:金属表面から飛び出した電子の速さ,$V_s$:阻止電圧,$W$:仕事関数
$eV_{s}=\dfrac{1}{2}mv^2=h\nu-W$
この式は意味を理解しましょう.光電子の運動エネルギーは阻止電圧を測定することで工夫してけいっだんができます.
★ グラフ
グラフは意味を考えて理解しましょう.また,上に出てきた式との比較も大事です.

コメント
[…] [式の意味を考えよう]光電効果 […]