対称性のある回路の合成抵抗3

問題

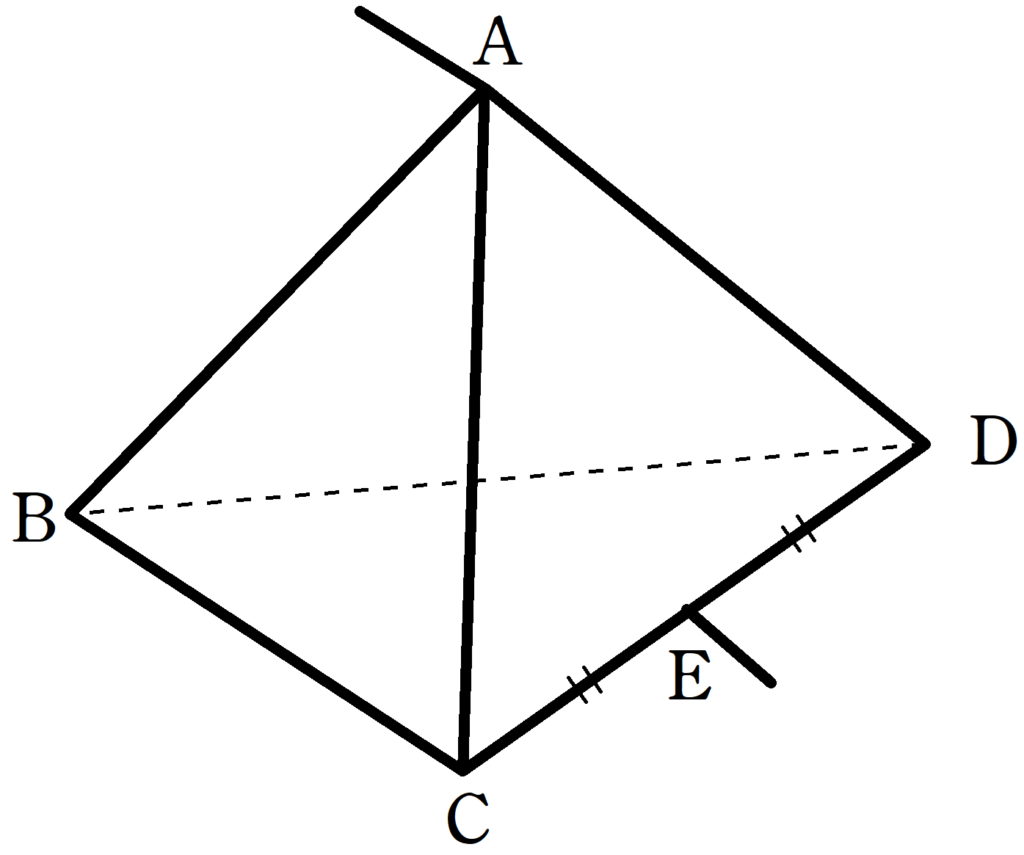
上図のような正四面体があり，AB，BC，BD，ADには抵抗値$R$の抵抗が，CE，DEには抵抗値$\dfrac{R}{2}$の抵抗がある．

このとき，AE間の合成抵抗を求めよ．

オームの法則

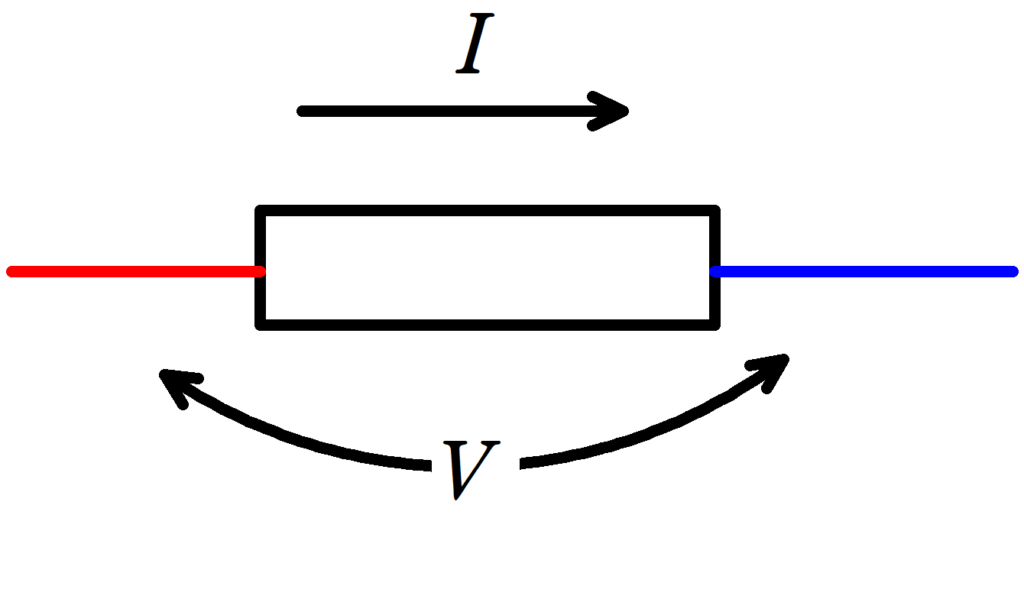
抵抗に流れる電流が$I$，電圧を$V$，抵抗値を$R$とするとき，

$V=RI$

が成り立つ．

合成抵抗を求めるときは，$\dfrac{V}{I}$を計算する．

PHYさん

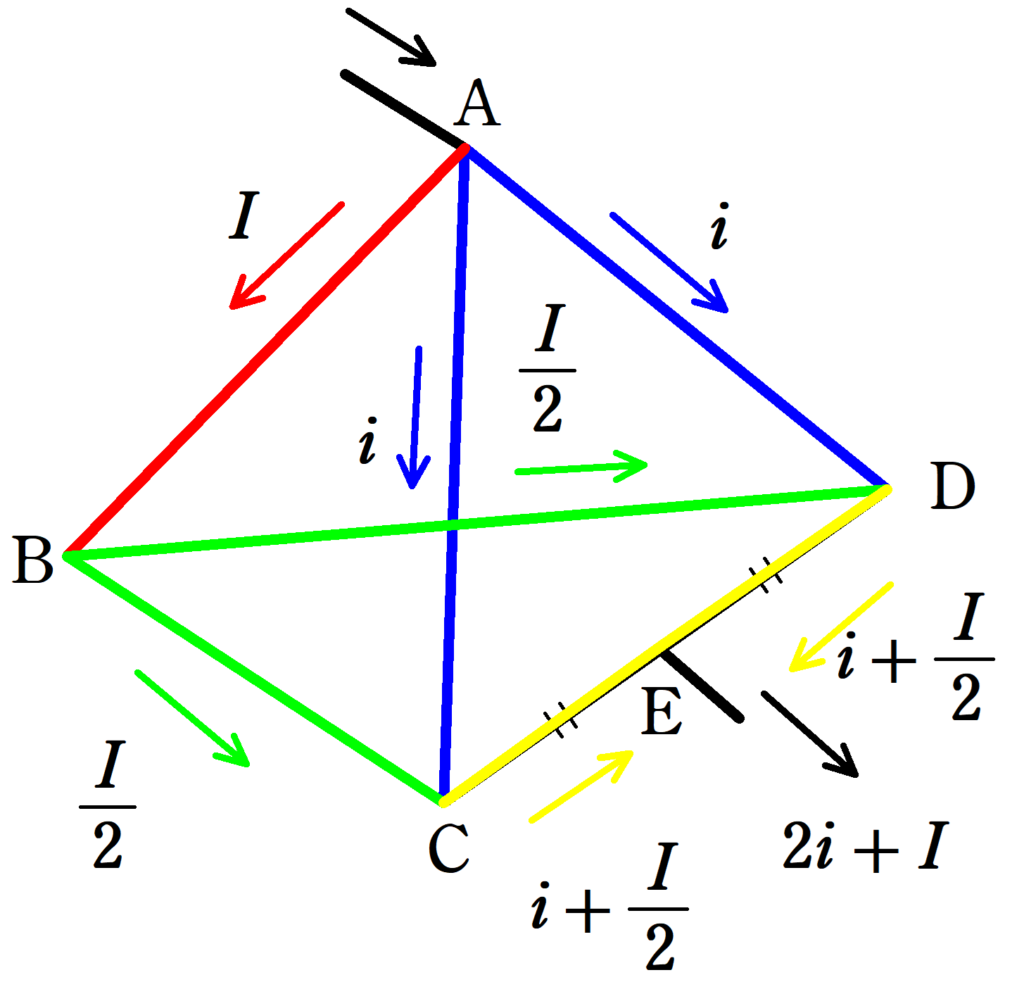
上図のように電流を設定しましょう．

対称性から，ACとADには同じ電流$i$が流れると考えます．

AB部分の電流は$I$としましょう．Ｂに到達した電流は，やはり対称性から，ＢＣ部分に$\dfrac{I}{2}$，ＢＤ部分に$\dfrac{I}{2}$の電流が流れます．

さらに，キルヒホッフ第1法則より，CE部分とDE部分にはそれぞれ，$i+\dfrac{I}{2}$が流れてＥから$2i+I$の電流が出ていきます．

Ｅの電位を$0$としたときのＡの電位を$V$として，求める合成抵抗は

$\dfrac{V}{2i+I}$

です．

★　A→Ｂ→Ｃ→Ｅの電圧降下の式

$V-RI-R\cdot \dfrac{I}{2}-\dfrac{R}{2}\cdot \left(i+\dfrac{I}{2}\right)=0$

$\therefore　\dfrac{7}{4}I+\dfrac{1}{2}i=\dfrac{V}{R}$　$\dots　(\ast)$

★　A→Ｃ→Ｅの電圧降下の式

$V-Ri-\dfrac{R}{2}\cdot \left(i+\dfrac{I}{2}\right)=0$

$\therefore　\dfrac{1}{4}I+\dfrac{3}{2}i=\dfrac{V}{R}$　$\dots　(2\ast)$

$(\ast)$，$(2\ast)$より

$I=\dfrac{2V}{5R}$，$i=\dfrac{3V}{5R}$

$2i+I=\dfrac{8V}{5R}$より，求める合成抵抗は，$\dfrac{V}{2i+I}=\dfrac{5}{8}R$ (答)