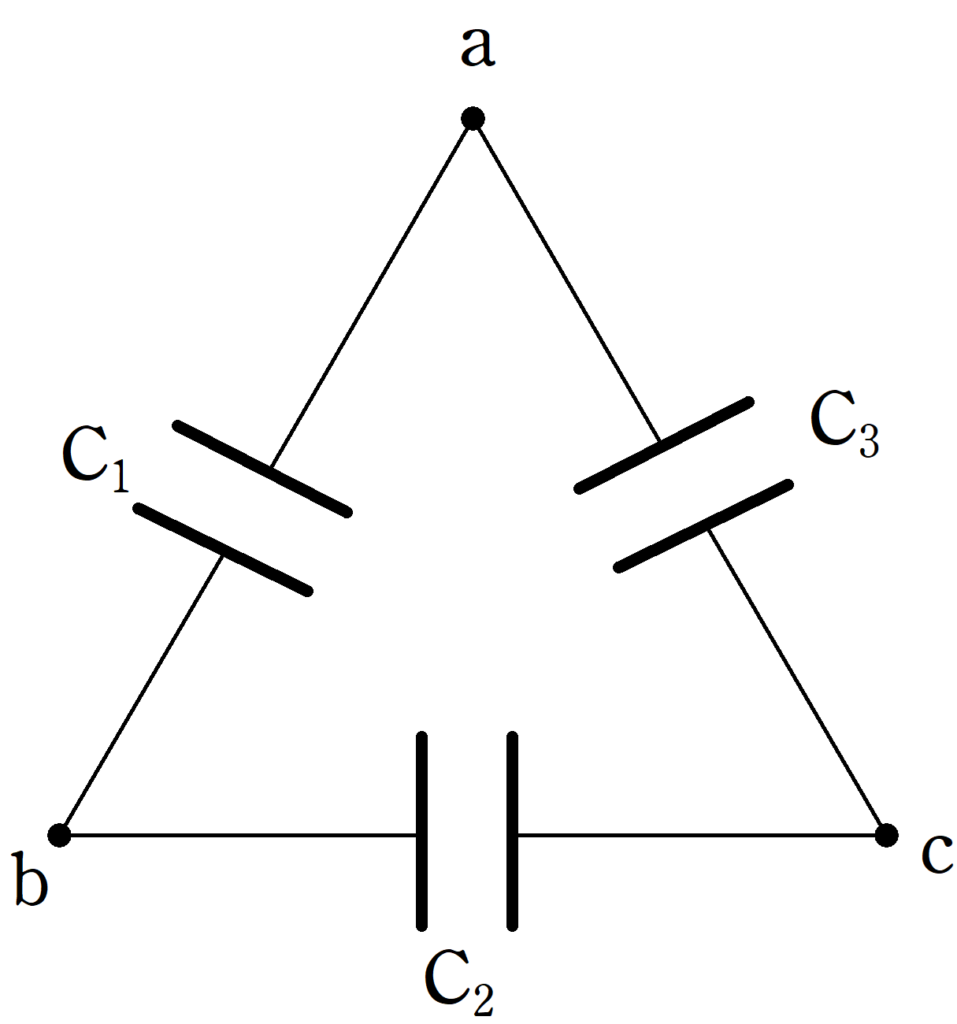
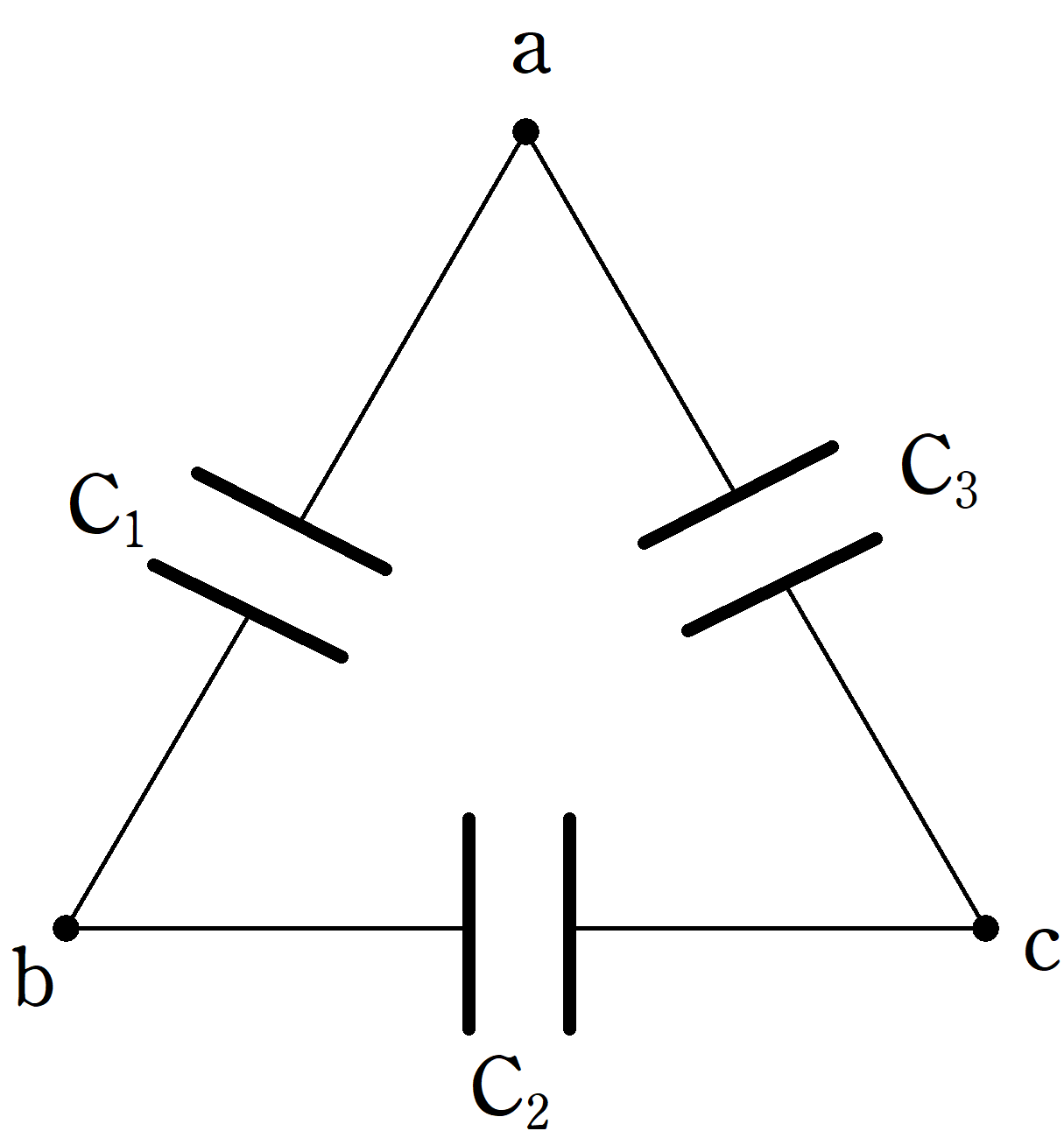
電荷保存則演習3 電位の設定2 | Physicmath（フィジクマス）

問題

上図のように，コンデンサー$\rm C_{1}$，$\rm C_{2}$，$\rm C_{3}$が接続してあり，それぞれの電気容量は$C$，$2C$，$3C$である．

はじめ，コンデンサーに電荷が蓄えられていない状態で次の操作①，②を行った．

<操作①>

上図のように，bを接地し，aが高電位，bが低電位になるように起電力$V$の電池をつなぎ，十分時間が経過した後に，電池を取り外した．

<操作②>

<操作①>に続いて，cを接地し，bが高電位，cが低電位になるように，起電力$V$の電池をつなぎ，十分時間が経過したあとに電池を取り外した．

問　<操作②>の後にそれぞれのコンデンサーに蓄えれている電荷を求めよ．

＜解答＞

NEKO

前回の内容はこちらです．

今回も

電荷保存則とコンデンサーの式

を立てて問題を解いていきましょう．

電気容量の定義式（コンデンサーの基本式）

コンデンサーに蓄えられている電荷を$Q$，コンデンサー間の電圧を$V$とすれば，コンデンサーの電気容量$C$は

$C=\dfrac{Q}{V}$

実際は

$Q=CV$

として使うことが多い．

電荷保存則

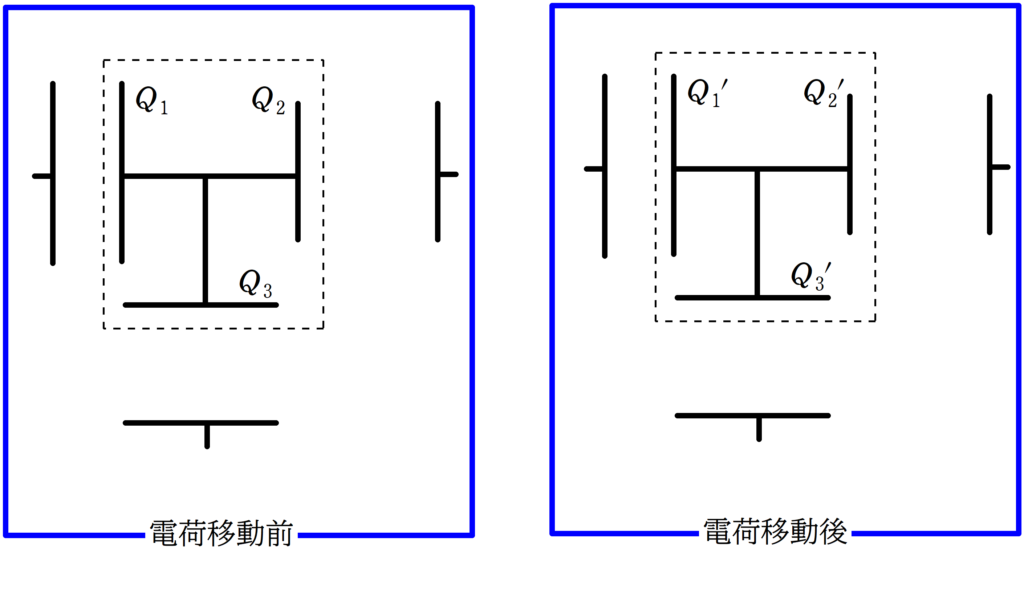
孤立した部分の電荷の総和は変化しない．これを電荷保存則という．

たとえば，上図のように点線部分の孤立した場所の電荷について考えると

$Q_{1}+Q_{2}+Q_{3}=Q_{1}^{\prime}+Q_{2}^{\prime}+Q_{3}^{\prime}$

が成り立つ．

NEKO

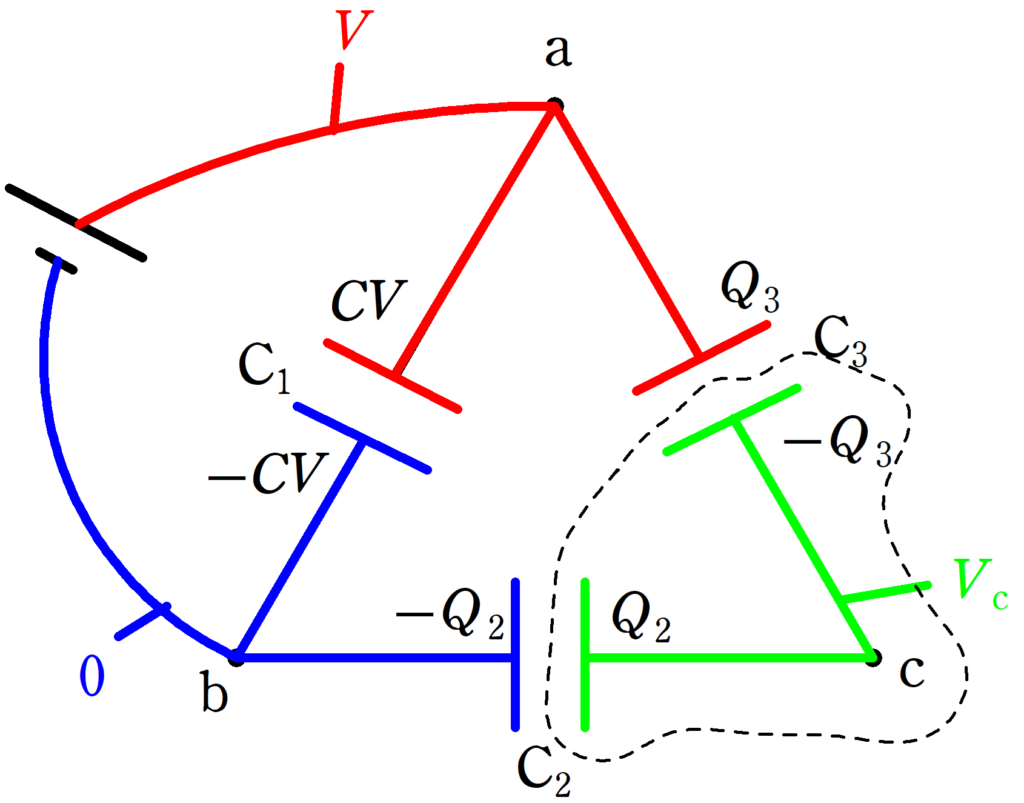
上図のように電荷と電位を設定します．

青の電位を基準の$0$として，赤い部分が$V$，緑色部分が$V_{c}$としています．

$\rm C_{1}$にかかる電圧は$V$と分かっているので，コンデンサーの基本式を用いれば，$CV$の電荷が蓄えられていることがわかります．

上図の点線部分の電荷保存則と，$\rm C_{2}$，$\rm C_{3}$のコンデンサーの式を立ててみましょう．

★　点線部分の電荷保存則

はじめ，電荷が蓄えられていないことに注意して

$0=-Q_{3}+Q_{2}$　$\dots　(\ast)$

★　コンデンサーの式

$Q_{2}=2C(V_{c}-0)=2CV_{c}$　$\dots　(2\ast)$

$Q_{3}=3C(V-V_{c})$　$\dots　(3\ast)$

$(2\ast)$，$(3\ast)$を$(\ast)$に代入して$V_{c}$を求めると

$0=-3C(V-V_{c})+2CV_{c}$

$\therefore　V_{c}=\dfrac{3}{5}V$　$\dots　(4\ast)$

$(4\ast)$を$(2\ast)$，$(3\ast)$に代入して

$Q_{2}=\dfrac{6}{5}CV$，$Q_{3}=\dfrac{6}{5}CV$

NEKO

ここまでが<操作①>です．

次に<操作②>です．

<操作①>で計算した電荷を符号含めて書くと下図の左のようになります．

NEKO

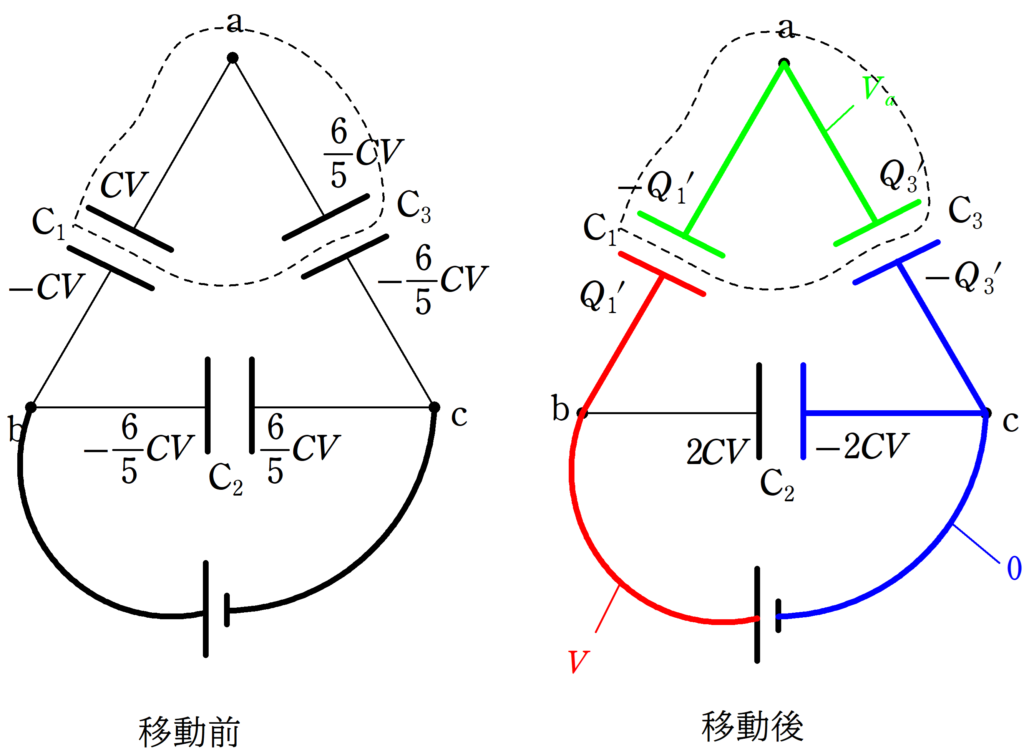
電荷移動後の電位と蓄えられた電荷は上図の右のように設定します．

青い部分を電位の基準である0として，赤い部分が$V$，緑部分の電位は$V_{a}$です．

電荷の符号は予想で設定しています．

（間違っていても正しい答えが出てくるので心配しなくても大丈夫です．）

また，$\rm C_{2}$にかかる電圧は$V$であることがわかっているで，コンデンサーの式より，蓄えれている電荷は$2CV$となります．

それでは，点線部分の電荷保存則と$\rm C_{1}$と$\rm C_{3}$のコンデンサーの式を立ててみましょう．

★　点線部分の電荷保存則

$CV+\dfrac{6}{5}CV=-Q_{1}^{\prime}+Q_{3}^{\prime}$　$\dots　(5\ast)$

★　コンデンサーの式

$Q_{1}^{\prime}=C(V-V_{a})$　$\dots　(6\ast)$

$Q_{3}^{\prime}=3C(V_{a}-0)=3CV_{a}$　$\dots　(7\ast)$

$(6\ast)$，$(7\ast)$を$(5\ast)$に代入して$V_{a}$を求めると

$\dfrac{11}{5}CV=-C(V-V_{a})+3CV_{a}$

$\therefore$　$V_{a}=\dfrac{4}{5}V$　$\dots　(8\ast)$

$(8\ast)$を$(6\ast)$，$(7\ast)$に代入して

$Q_{1}^{\prime}=\dfrac{1}{5}CV$

$Q_{3}^{\prime}=\dfrac{12}{5}CV$

NEKO

計算の結果，$\rm C_{1}$に蓄えられた電荷は$\dfrac{1}{5}CV$，$\rm C_{2}$に蓄えられた電荷は$2CV$，$\rm C_{3}$に蓄えられた電荷は$\dfrac{12}{5}CV$，となることがわかりました．

このように，何度も電池やスイッチをつなぎ変える問題は，途中経過において，どちらの極板が正の電荷でどちらの極板が負の電荷かなのかまで気にして計算をする必要があります．