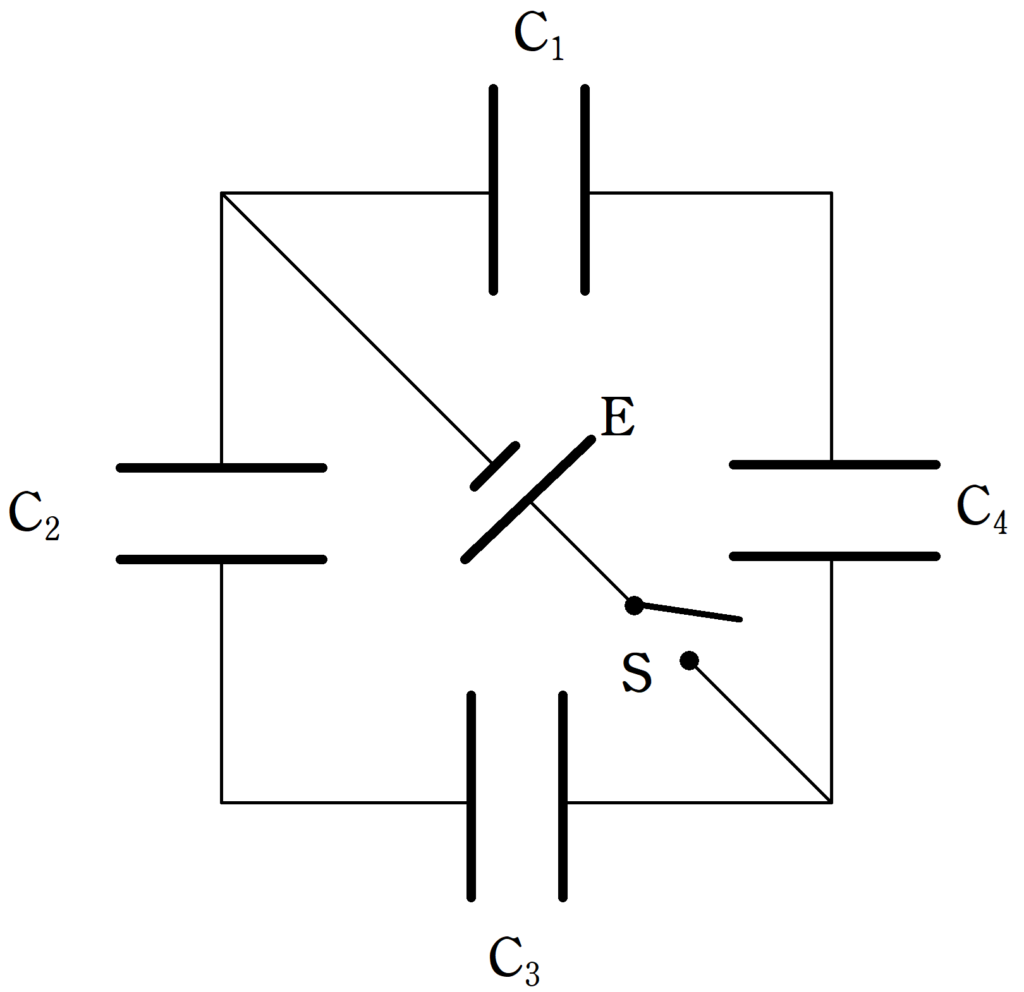
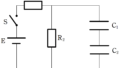
電荷保存則演習4 電位の設定3 | Physicmath（フィジクマス）

問題

電気容量$C$，$2C$，$3C$，$4C$のコンデンサー$\rm C_{1}$，$\rm C_{2}$，$\rm C_{3}$，$\rm C_{4}$と起電力$V$の電池$\rm E$，スイッチ$\rm S$が上図のように接続されている．

はじめ，スイッチは開いており，各コンデンサーには電荷が蓄えられていなかった．

この状態から，スイッチを閉じて十分時間が経った後にコンデンサー$\rm C_{1}$，$\rm C_{2}$，$\rm C_{3}$，$\rm C_{4}$に蓄えられた電荷を求めよ．

NEKO

前回の問題はこちらです．

今回も，電荷保存則とコンデンサーの式を用いて問題を解きます．

電気容量の定義式（コンデンサーの基本式）

コンデンサーに蓄えられている電荷を$Q$，コンデンサー間の電圧を$V$とすれば，コンデンサーの電気容量$C$は

$C=\dfrac{Q}{V}$

実際は

$Q=CV$

として使うことが多い．

電荷保存則

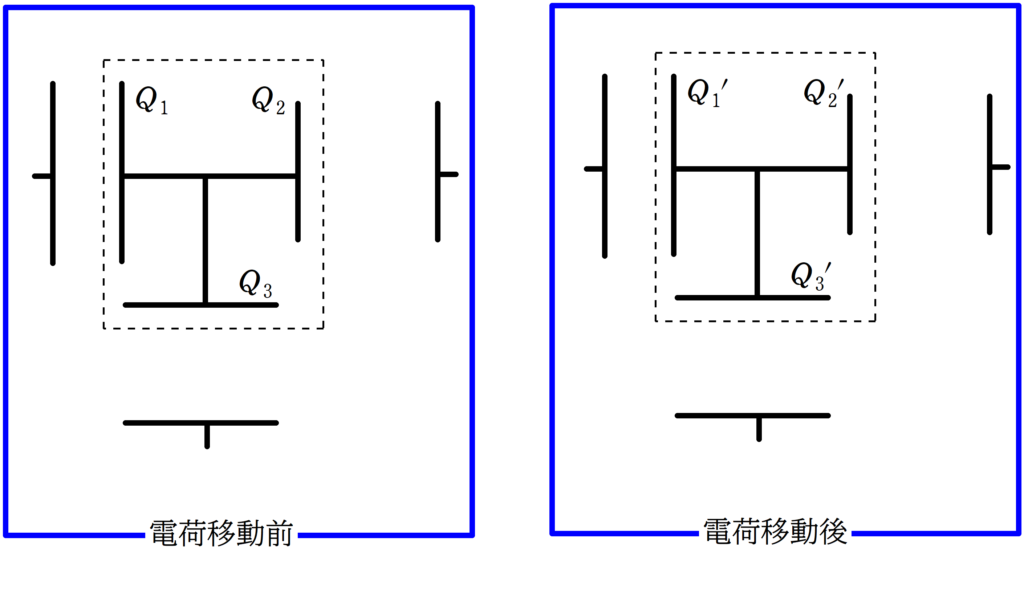
孤立した部分の電荷の総和は変化しない．これを電荷保存則という．

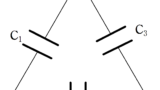
たとえば，上図のように点線部分の孤立した場所の電荷について考えると

$Q_{1}+Q_{2}+Q_{3}=Q_{1}^{\prime}+Q_{2}^{\prime}+Q_{3}^{\prime}$

が成り立つ．

NEKO

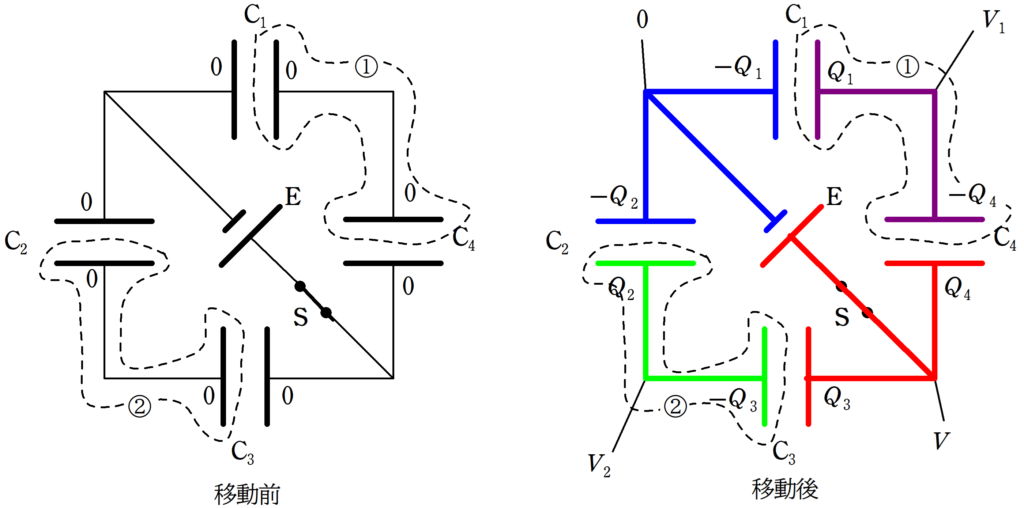
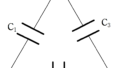
スイッチを閉じて十分時間が経ち，電荷が移動した後の各コンデンサーに蓄えれた電荷と電位をそれぞれ，上右図のように設定します．

電位は，青い部分が基準の0，赤い部分は電池の起電力が$V$であることから$V$，紫部分を$V_{1}$，緑色部分を$V_{2}$としています．

①と②の点線部分の電荷保存則と，各コンデンサーのコンデンサーの式を立てましょう．

★　電荷保存則

①の電荷保存則

$0=Q_{1}-Q_{4}$　$\therefore　Q_{1}=Q_{4}$　$\dots　(\ast)$

②の電荷保存則

$0=Q_{2}-Q_{3}$　$\therefore　Q_{2}=Q_{3}$　$\dots　(2\ast)$

★　コンデンサーの式

$Q_{1}=CV_{1}$　$\dots　(\spadesuit)$

$Q_{2}=2CV_{2}$　$\dots　(2\spadesuit)$

$Q_{3}=3C(V-V_{2})$　$\dots　(3\spadesuit)$

$Q_{4}=4C(V-V_{1})$　$\dots　(4\spadesuit)$

$(\spadesuit)$～$(4\spadesuit)$を$(\ast)$と$(2\ast)$に代入して$V_{1}$と$V_{2}$を求める．

$CV_{1}=4C(V-V_{1})$

$\therefore　V_{1}=\dfrac{4}{5}V$　$\dots　(3\ast)$

$2CV_{2}=3C(V-V_{2})$

$V_{2}=\dfrac{3}{5}V$　$\dots　(4\ast)$

$(3\ast)$と$(4\ast)$を$(\spadesuit)$～$(4\spadesuit)$に代入すると

$Q_{1}=\dfrac{4}{5}CV$

$Q_{2}=\dfrac{6}{5}CV$

$Q_{3}=\dfrac{6}{5}CV$

$Q_{4}=\dfrac{4}{5}CV$