twitterの問題26の解答

<問題>

＜解答＞

以下の式を使う．

半減期の式

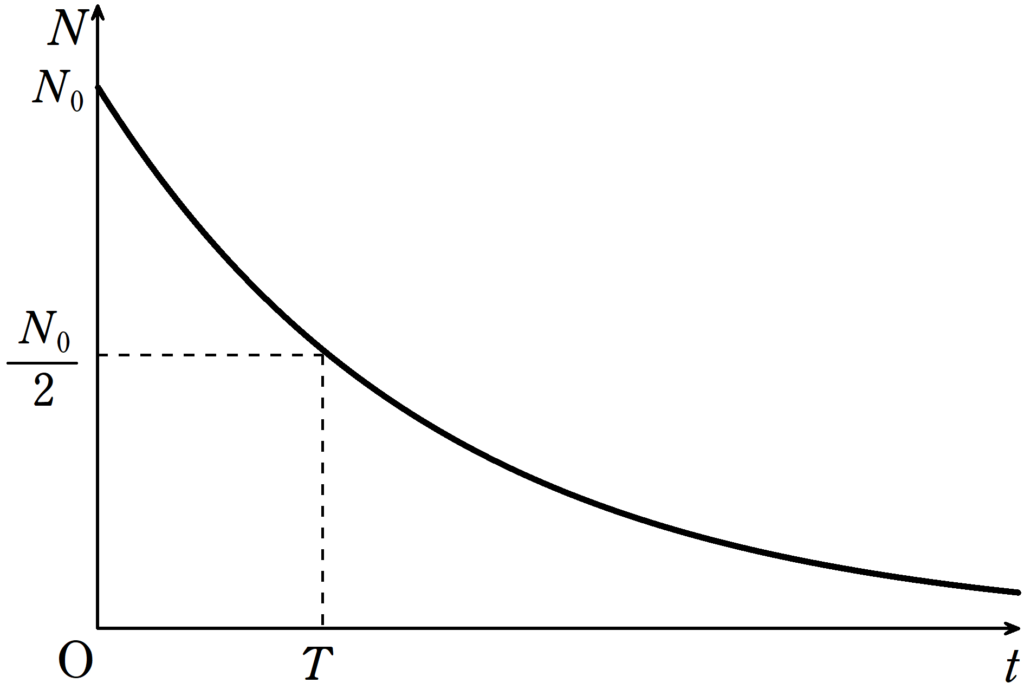
時刻$t=0$における放射性元素の数を$N_{0}$とする．時刻$t$における放射性元素の数を$N(t)$とする．半減期（放射性元素の数が半分になるまでの時間）を$T$とすると，次の式が成り立つ．

$N(t)=N_{0}\left(\dfrac{1}{2}\right)^{\frac{t}{T}}$

$^{12}_{\,\,6}{\rm C}$は変化しないと書かれていて，$\dfrac{^{14}_{\,\,6}{\rm C}}{^{12}_{\,\,6}{\rm C}}$が$0.71\left(\fallingdotseq \dfrac{1}{\sqrt{2}}\right)$倍になっているので，$^{14}_{\,\,6}{\rm C}$の数が$0.71\left(\fallingdotseq \dfrac{1}{\sqrt{2}}\right)$倍になったと考えることができる．

つまり，半減期の式

$N(t)=N_{0}\left(\dfrac{1}{2}\right)^{\frac{t}{T}}$

において，$\dfrac{N}{N_{0}}=\dfrac{1}{\sqrt{2}}$，$T=5700$を代入して

$\dfrac{1}{\sqrt{2}}=\left(\dfrac{1}{2}\right)^{\frac{t}{5700}}$

上式の左辺は$\left(\dfrac{1}{2}\right)^{\frac{1}{2}}$であるから

$\left(\dfrac{1}{2}\right)^{\frac{1}{2}}=\left(\dfrac{1}{2}\right)^{\frac{t}{5700}}$

$\therefore\,\, \dfrac{1}{2}=\dfrac{t}{5700}$　$\therefore\,\, t=\dfrac{5700}{2}=2.9\times 10^{3}\,$年　(答)