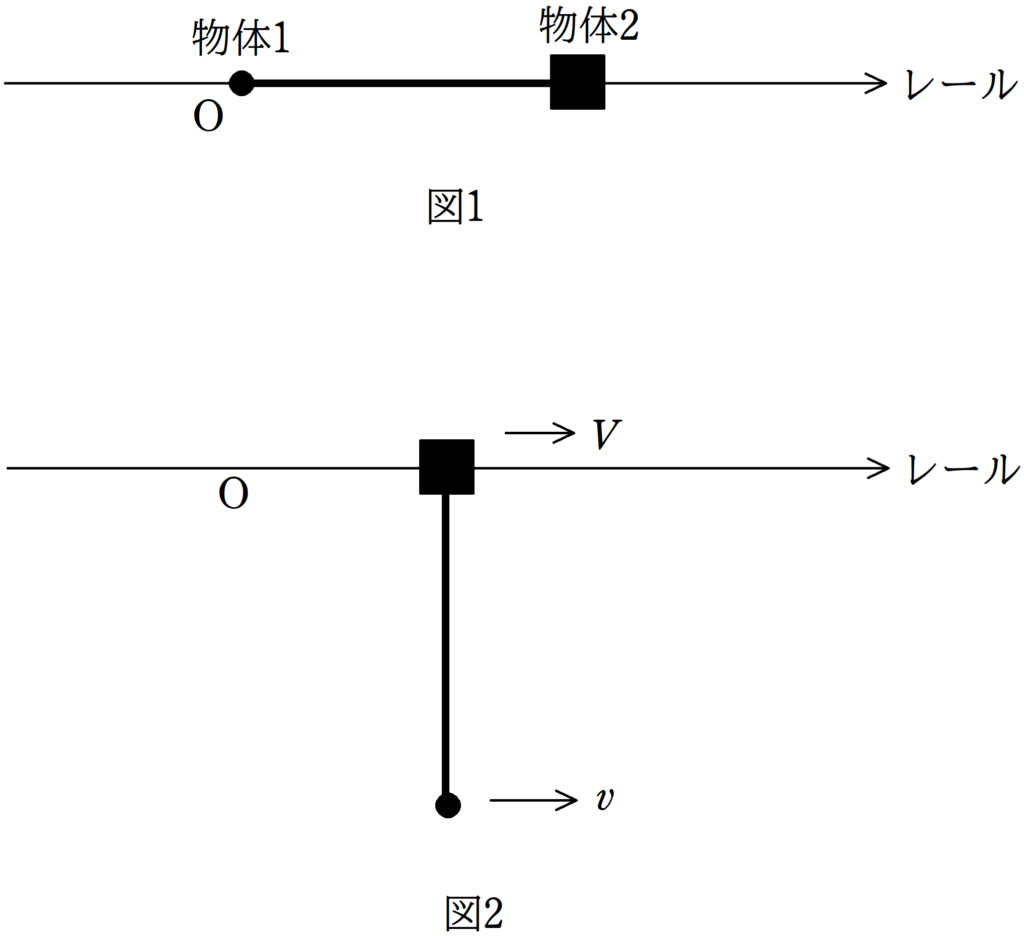
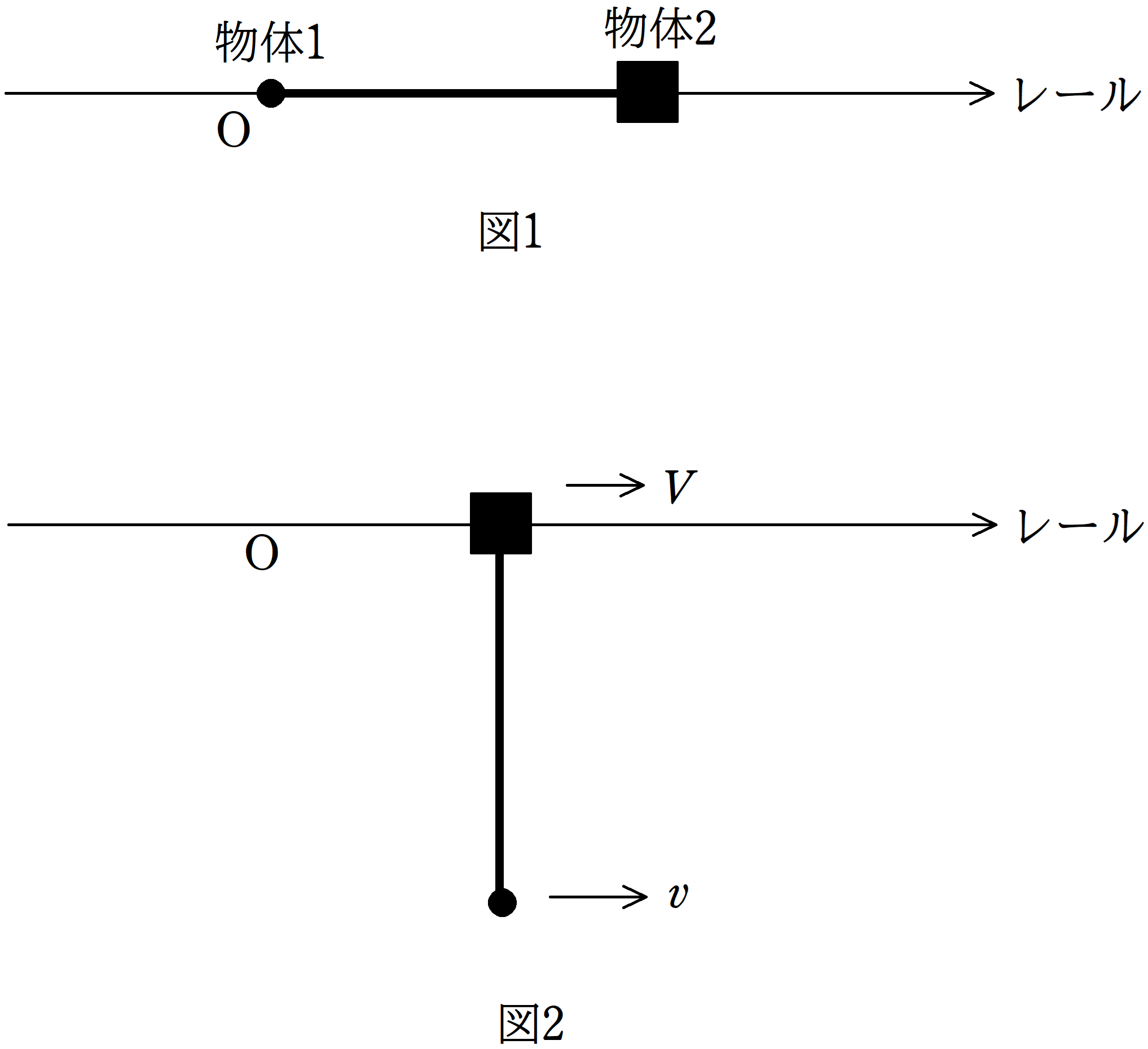
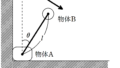
図1のように,固定したレールがあり,物体2はレール上をなめらかに動くことができる.
物体2の質量は$M$であり,物体2には軽くて伸びない長さ$l$の糸がつながれている.
糸の他端には質量$m$の物体1が取りつけられている.物体1をレールと同じ高さまでもっていき,糸を張った.物体1と物体2の静止した状態から静かに手をはなすと,物体1は物体2に対して同一平面内を円運動し,物体2はレール上を動く.重力加速度の大きさを$g$として,次の問いに答えよ.ただし,図1の状態における物体1の位置を原点として,図の水平右向きに座標をとる.
(1) 水平右向きを速度の正の向きとする.糸は常に張っている状態で運動しているとして,物体1がはじめて最下点に達したときの物体1の速度$v$と物体2の速度$V$をそれぞれ$M$,$m$,$g$,$l$から必要なものを用いて表せ.
(2) 物体がはじめて最下点に達したときの張力の大きさ$T$を$m$,$M$,$g$,$l$を用いて表せ.
(3) 運動中,物体1と物体2にはたらく水平方向の力は常に0である.このことを用いて,物体1が最下点に達したときの物体1と2の$x$座標は一致している.このときの座標$x^{\prime}$を$M$,$m$,$l$を用いて表せ.
<解答>

この問題は上で扱った問題とほぼ同じだね.
水平方向の運動量保存則と力学的エネルギー保存則を立てます.
★ 運動量保存則
$0=mv+MV$ $\dots (\ast)$
★ 力学的エネルギー保存則
$mgl=\dfrac{1}{2}mv^{2}+\dfrac{1}{2}MV^{2}$ $\dots (2\ast)$

$(\ast)$と$(2\ast)$より,$v$と$V$を求めます.
$(\ast)$より
$v=-\dfrac{M}{m}V$ $\dots (3\ast)$
$(3\ast)$を$(2\ast)$に代入すると
$\eqalign{\dfrac{1}{2}m\left(-\dfrac{M}{m}V\right)^{2}+\dfrac{1}{2}MV^{2}&=mgl\cr \dfrac{1}{2}MV^{2}\left(\dfrac{M}{m}+1\right)&=mgl\cr \dfrac{1}{2}MV^{2}\cdot \dfrac{M+m}{m}&=mgl \cr V^{2}&=\dfrac{2m^{2}gl}{M(M+m)}}$
$\therefore V=-m\sqrt{\dfrac{2gl}{M(M+m)}}$ (答) $\dots (4\ast)$
さらに,$(4\ast)$を$(3\ast)$に代入すると
$v=M\sqrt{\dfrac{2gl}{M(M+m)}}$ (答)
(2)

今回も張力の大きさは$mg$ではないことに注意してください.
床で止まっている人から見ると複雑な運動なので,物体2の上から物体の運動を観測しましょう.
物体2からみると,物体1は円運動しています.
なので,物体2からみた円運動の運動方程式を立てましょう.
半径$r$,円運動の接線方向の速さを$v$,角速度を$\omega$とすると,向心加速度の大きさ$a$は
$a=\dfrac{v^{2}}{r}=r\omega^{2}$
向心加速度の向きは円運動の中心
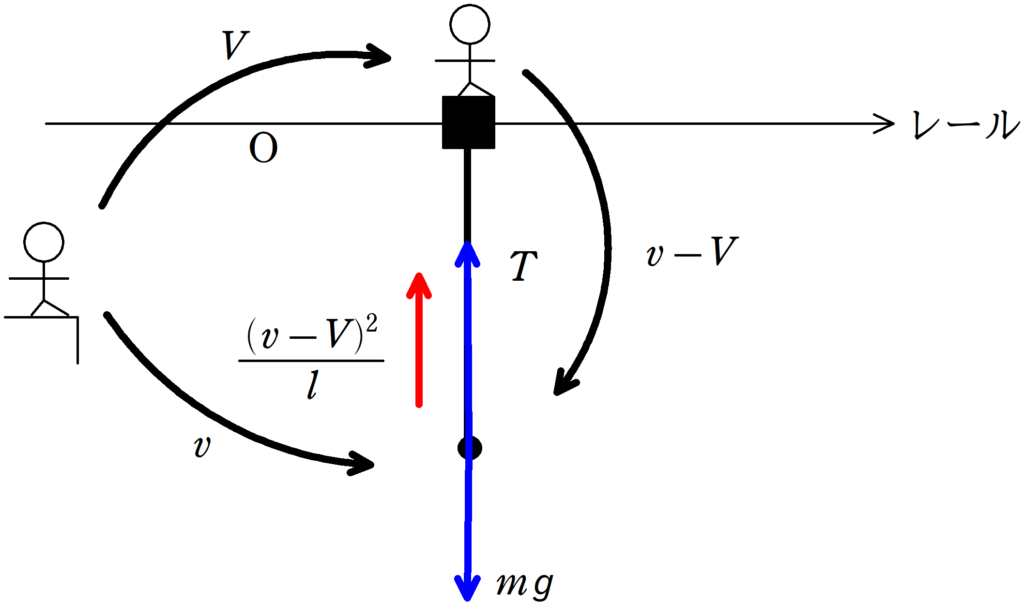
物体2からみた物体1の速度は$v-V$なので
$\eqalign{v-V&=M\sqrt{\dfrac{2gl}{M(M+m)}}-\left(-m\sqrt{\dfrac{2gl}{M(M+m)}}\right)\\&=(M+m)\sqrt{\dfrac{2gl}{M(M+m)}}\\&=\sqrt{\dfrac{2(M+m)gl}{M}}}$
したがって,物体2からみた物体1の向心方向の運動方程式より
$m\dfrac{(v-V)^{2}}{l}=T-mg$
$\eqalign{T&=mg+m\dfrac{(v-V)^{2}}{l}\\&=mg+m\dfrac{1}{\cancel{l}}\dfrac{2(M+m)g\cancel{l}}{M}\\&=\left(\dfrac{2(M+m)}{M}+1\right)mg\\&=\dfrac{3M+2m}{M}mg}$
したがって,$T=\dfrac{3M+2m}{M}mg$(答)
(3)

最後は重心不変を利用します.
重心不変の問題はこちらでも紹介しています.
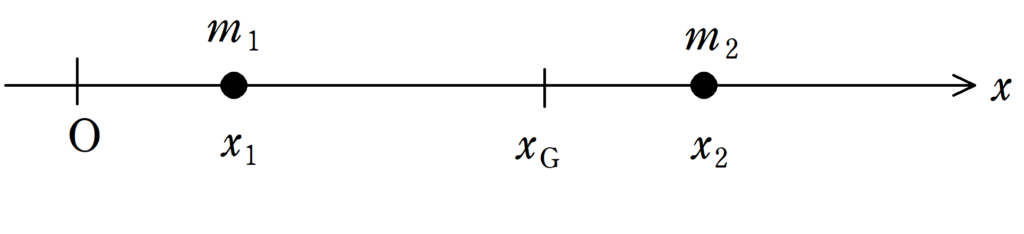
$x$軸上に質量$m_{1}$と$m_{2}$の物体がある.それぞれの座標を$x_{1}$,$x_{2}$とすると,その重心座標$x_{\rm G}$は
$x_{\rm G}=\dfrac{m_{1}x_{1}+m_{2}x_{2}}{m_{1}+m_{2}}$
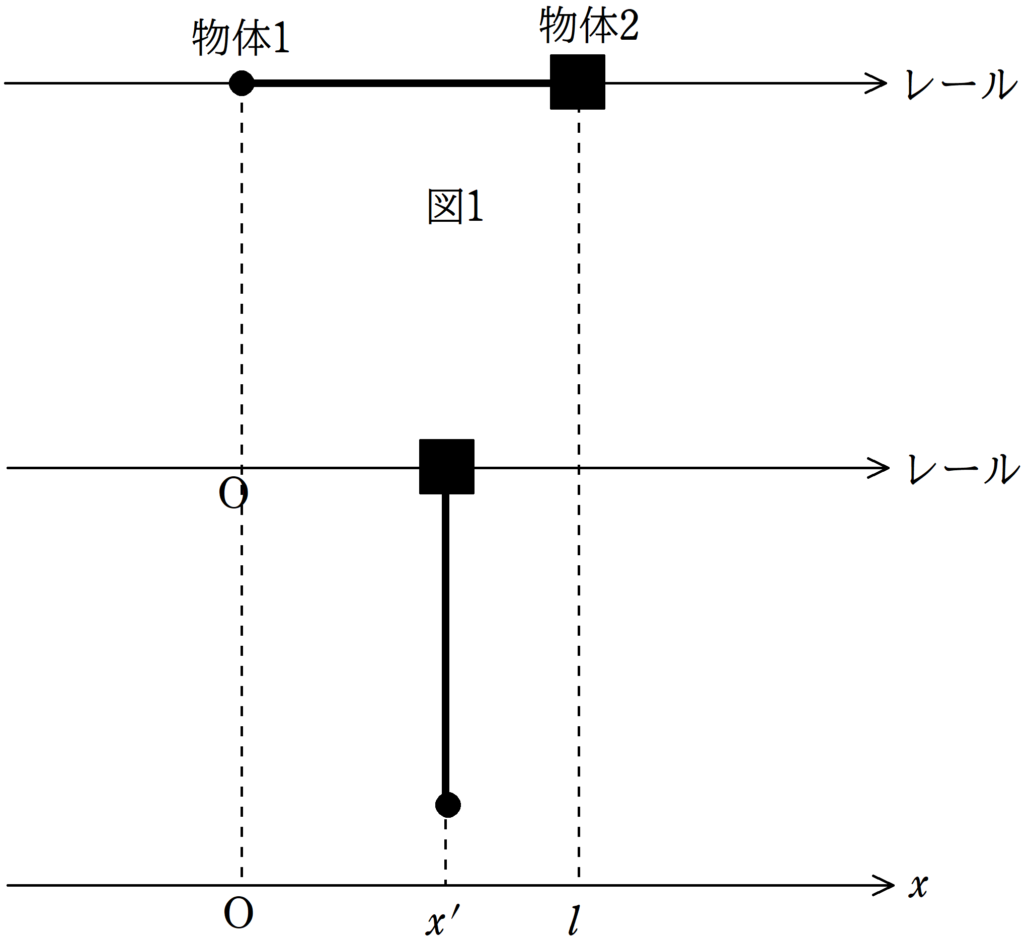
★ 重心不変の式
$\dfrac{m\cdot 0+M\cdot l}{M+m}=\dfrac{mx^{\prime}+Mx^{\prime}}{M+m}$
$\therefore x^{\prime}=\dfrac{M}{M+m}l$ (答)

コメント