
前回の内容はこちらです.
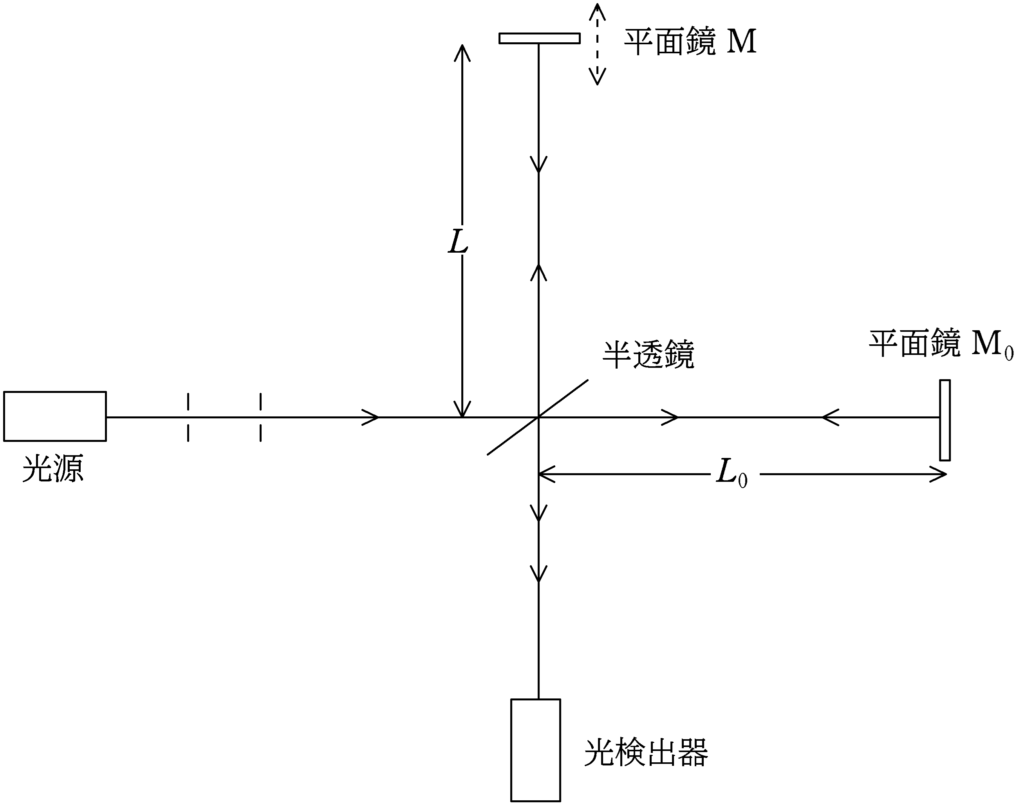
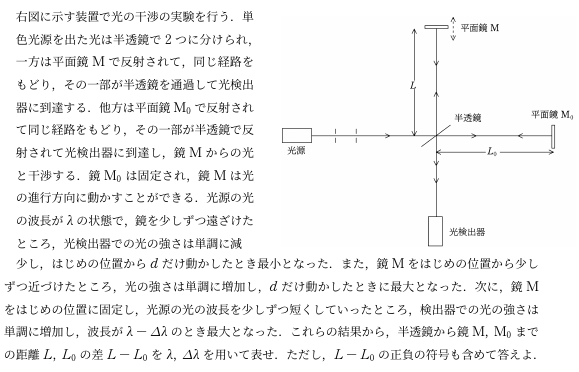
図に示す装置で光の干渉の実験を行う.単色光源を出た光は半透鏡で2つに分けられ,一方は平面鏡$\rm M$で反射されて,同じ経路をもどり,その一部が半透鏡を通過して光検出器に到達する.他方は平面鏡$\rm M_{0}$で反射されて同じ経路をもどり,その一部が半透鏡で反射されて光検出器に到達し,鏡$\rm M$からの光と干渉する.鏡$\rm M_{0}$は固定され,鏡$\rm M$は光の進行方向に動かすことができる.光源の光の波長が$\lambda$の状態で,鏡$\rm M$を少しずつ遠ざけたところ,光検出器での光の強さは単調に減少し,はじめの位置から$d$だけ動かしたとき最小となった.また,鏡$\rm M$をはじめの位置から少しずつ近づけたところ,光の強さは単調に増加し,$d$だけ動かしたときに最大となった.次に,鏡$\rm M$をはじめの位置に固定し,光源の光の波長を少しずつ短くしていったところ,検出器での光の強さは単調に増加し,波長が$\lambda-\varDelta \lambda$のとき最大となった.これらの結果から,半透鏡から鏡$\rm M,M_{0}$までの距離$L,L_{0}$の差$L-L_{0}$を$\lambda,\varDelta \lambda$を用いて表せ.ただし,$L-L_{0}$の正負の符号も含めて答えよ.

干渉による位相差の条件をまとめると次のようになります.
地点Pにおける2つの波の位相差を$\phi$,整数を$m$とすると,
強め合いの条件:$\phi=2\pi m$
弱め合いの条件:$\phi=(2m+1)\pi $
位相差$\phi$は次の3つの要素で決まる.
$\phi_{1}$:初期位相のずれ
同位相なら$\phi_{1}=0$,逆位相なら$\phi_{1}=\pi$
$\phi_{2}$:反射による位相のずれ
自由端反射なら$\phi_{2}=0$,固定端反射なら$\phi_{2}=\pi$
$\phi_{3}$:距離の差(屈折率が変わることで生じる光学的な距離の差を含む)による位相のずれ
距離の差が$\Delta l$のとき,次の比例式を立てて,位相差$\phi_{3}$を計算する.
$2\pi : \lambda =\phi_{3} : \Delta l$
$\therefore \phi_{3}=\dfrac{2\pi}{\lambda}\Delta l$
このとき,位相差$\phi$は
$\phi=\phi_{1}+\phi_{2}+\phi_{3}$
<解答>

前半部分で
- 鏡$\rm M$を少しずつ遠ざけたところ,光検出器での光の強さは単調に減少し,はじめの位置から$d$だけ動かしたとき最小となった.(実験①)
- 鏡$\rm M$をはじめの位置から少しずつ近づけたところ,光の強さは単調に増加し,$d$だけ動かしたときに最大となった.(実験②)
とあるので,これを式にしていきましょう.
※ 実際は半透鏡での反射によって,2経路の位相差が$\pi$分ずれ,強め合いの条件と弱め合いの条件が真逆になりますが,差をとると同じ答えが出ます.
・実験①について
経路差は往復分も考えて,$2\left(L+d-L_{0}\right)$なので,位相差は$\dfrac{2\pi}{\lambda}\left\{2\left(L+d-L_{0}\right)\right\}$.整数$m$を用いて,弱め合いの条件より
$\dfrac{2\pi}{\lambda}\left\{2\left(L+d-L_{0}\right)\right\}=2\pi m+\pi \cdots (\ast)$
・実験②について
経路差は往復分も考えて,$2\left(L-d-L_{0}\right)$なので,位相差は$\dfrac{2\pi}{\lambda}\left\{2\left(L-d-L_{0}\right)\right\}$.実験①に比べて位相差が小さくなっている.$2\pi m+\pi$より位相差が小さく,強め合う位相差は$2\pi m$なので,強め合いの条件より
$\dfrac{2\pi}{\lambda}\left\{2\left(L-d-L_{0}\right)\right\}=2\pi m \cdots (2\ast)$

$(\ast)-(2\ast)$を計算すると,邪魔な$m$が消えて,$d$を求めることができます.
★ $(\ast)-(2\ast)$より
$\dfrac{2\pi}{\lambda}\times 4d=\pi$
$\therefore\,\, d=\dfrac{\lambda}{8}$ $\cdots (3\ast)$

最後に
- 鏡$\rm M$をはじめの位置に固定し,光源の光の波長を少しずつ短くしていったところ,検出器での光の強さは単調に増加し,波長が$\lambda-\varDelta \lambda$のとき最大となった. (実験③)
より,強め合いの条件を立てます.
鏡$\rm M$がはじめの位置にあるときは,検出器での位相差が$2\pi m$と$2\pi m+\pi$の間にありました.この状態から,波長を小さくしていくので,
$\dfrac{2\pi}{\lambda}\times (経路差)$
より,$\lambda$が小さくなると,
経路差が正のとき,位相差が$0$から離れて大きくなり
経路差が負のとき,位相差が$0$から離れて小さくなる
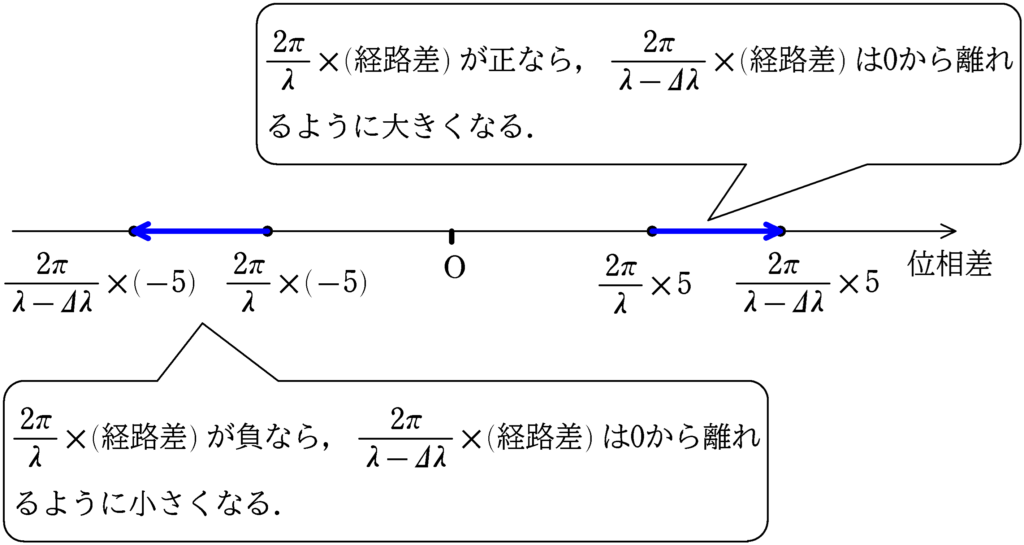
もう一度話を戻すと,「検出器での位相差が$2\pi m$と$2\pi m+\pi$の間にあった」状態から,波長を小さくしていくと,強め合ったので,位相差が$2\pi m$になったことがわかります.$2\pi m+\pi$になってしまうと一度弱め合ってしまいます.つまり,この時点で経路差$2(L-L_{0})$は負であることがわかります.ただ,わざわざこの考察はしなくても計算によって,経路差の正負は出てきます.
★ 波長を$\lambda-\varDelta \lambda$にしたときの強め合いの条件
$\dfrac{2\pi}{\lambda-\varDelta \lambda}\{2(L-L_{0})\}=2\pi m \cdots (4\ast)$
$(2\ast)$,$(3\ast)$より,$2\pi m$を消去します.
$\dfrac{\cancel{2\pi}}{\lambda-\varDelta \lambda}\{\bcancel{2}(L-L_{0})\}=\dfrac{\cancel{2\pi}}{\lambda}\left\{\bcancel{2}\left(L-d-L_{0}\right)\right\}$
両辺$\lambda(\lambda-\varDelta \lambda)$をかけて
$\lambda(L-L_{0})=(\lambda-\varDelta \lambda)(L-L_{0}-d)$
$\therefore\,\, \varDelta \lambda(L-L_{0})=-(\lambda-\varDelta \lambda)d$
$(3\ast)$から,$d=\dfrac{\lambda}{8}$より
$\eqalign{\varDelta \lambda(L-L_{0})&=-(\lambda-\varDelta \lambda)\times \dfrac{\lambda}{8}\\\cr L-L_{0}&=-\dfrac{(\lambda-\varDelta \lambda)\lambda}{8\varDelta \lambda}}$(答)

このように,$L-L_{0}$が確かに負であることが確かめられました.



コメント