※ 問題文訂正 「ただし,電場の大きさは$E$とする.」を追加.
<解答>
まずは,速さの最大値と最小値から.
ローレンツ力は仕事をしないので,運動エネルギーの変化に影響はない.
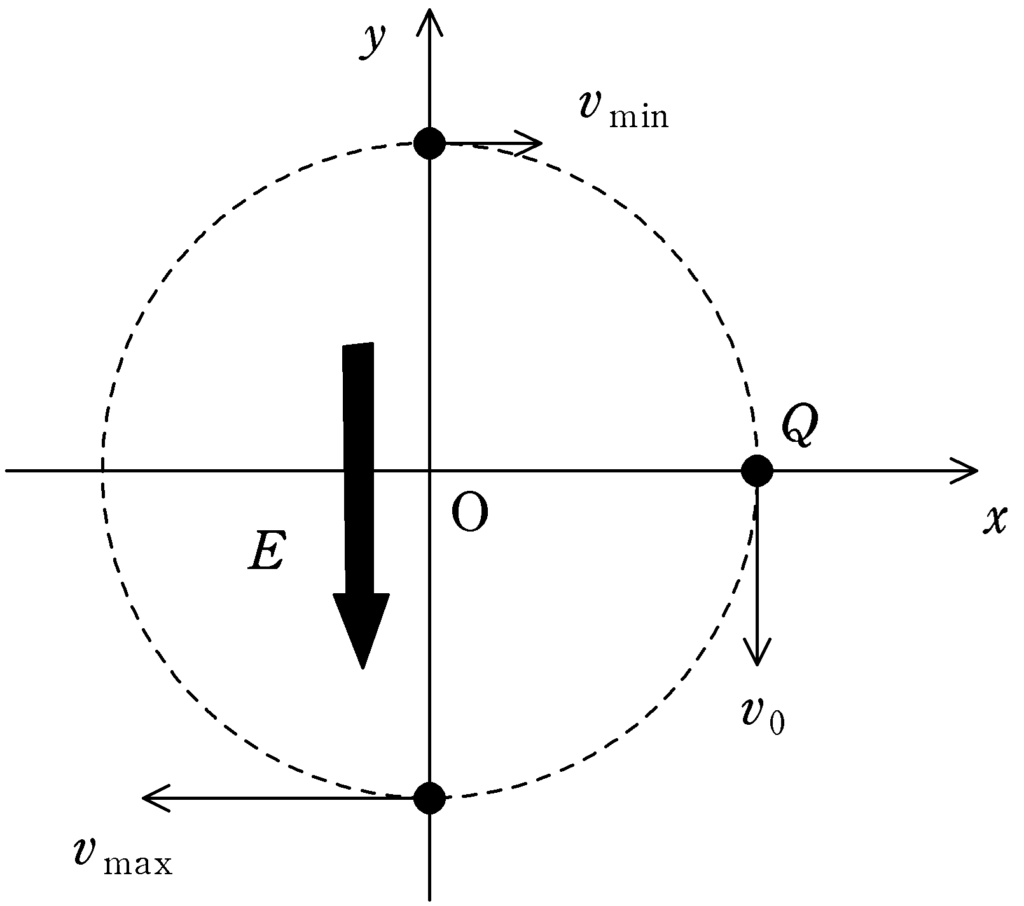
小球には常に$y$軸負の方向に大きさ$QE$の静電気力がはたらいているので,座標$(0,-l)$にいるときに速さが最大となって,座標$(0,l)$にいるとき,速さは最小となる.
※重力が$y$軸負の方向にはたらきながら円運動をするときをイメージすればよい.
速さの最大値を$v_{\rm max}$,最小値を$v_{\rm min}$とし,運動エネルギーの変化と外力(静電気力)がした仕事の関係式を立てると,
$\dfrac{1}{2}mv_{\rm max}^{2}-\dfrac{1}{2}mv_{0}^{2}=QEl$
$\therefore\,\, v_{\rm max}=\sqrt{v_{0}^{2}+\dfrac{2QEl}{m}}$(答)
同様にして最小値も考える.静電気力が負の仕事をしていることに注意.
$\dfrac{1}{2}mv_{\rm min}^{2}-\dfrac{1}{2}mv_{0}^{2}=-QEl$
$\therefore\,\, v_{\rm min}=\sqrt{v_{0}^{2}-\dfrac{2QEl}{m}}$(答)
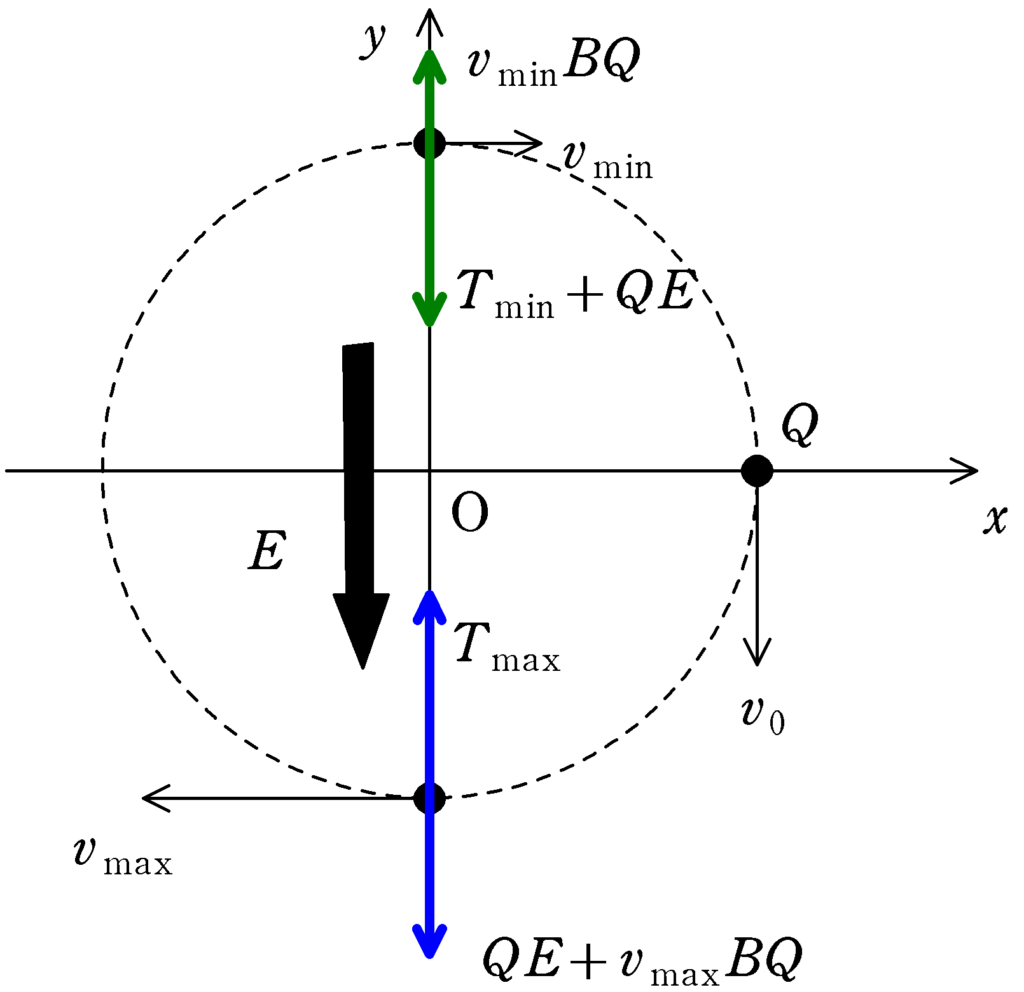
次に張力について,最も気をつけなくてはいけなことは,ローレンツ力の向き.たとえば,$(l,0)$に小球がある場合,$y$軸負の方向に速度(左手中指)をもっていて,磁場が$z$軸負(左手中指)の方向なので,ローレンツ力は$x$軸正の向き(左手親指)を向く.このように,この問題では,ローレンツ力は常に円運動の中心方向と反対方向にローレンツ力がはたらく.
張力が一番大きくなるところは$(0,-l)$に小球があるとき(張力とは反対方向に静電気力,ローレンツ力(しかも速さ最大なので,ローレンツ力の大きさも最大),小球とともに回転している系だと遠心力もはたらき,張力が最大値になることがわかる)であり,中心方向に張力$T_{\rm max}$,中心とは反対方向に静電気力とローレンツ力の和$QE+v_{\rm max}BQ$がはたらくので,向心方向の運動方程式より
$m\dfrac{v_{\rm max}^{2}}{l}=T_{\rm max}-QE-v_{\rm max}BQ$
$v_{\rm max}=\sqrt{v_{0}^{2}+\dfrac{2QEl}{m}}$より
$\eqalign{T_{\rm max}&=QE+v_{\rm max}BQ+m\dfrac{v_{\rm max}^{2}}{l}\\&=QE+BQ\sqrt{v_{0}^{2}+\dfrac{2QEl}{m}}+\dfrac{m}{l}\times \left(v_{0}^{2}+\dfrac{2QEl}{m}\right)\\&=\dfrac{mv_{0}^{2}}{l}+Q\left\{3E+B\sqrt{v_{0}^{2}+\dfrac{2QEl}{m}}\right\}}$(答)
また,張力が最小になるのは,$(0,l)$に小球があるときであり,このときの張力を$T_{\rm min}$とする.向心方向の運動方程式より
$m\dfrac{v_{\rm min}^{2}}{l}=T_{\rm min}+QE-v_{\rm min}BQ$
$v_{\rm min}=\sqrt{v_{0}^{2}-\dfrac{2QEl}{m}}$より
$\eqalign{T_{\rm min}&=-QE+v_{\rm min}BQ+m\dfrac{v_{\rm min}^{2}}{l}\\&=-QE+BQ\sqrt{v_{0}^{2}-\dfrac{2QEl}{m}}+\dfrac{m}{l}\times \left(v_{0}^{2}-\dfrac{2QEl}{m}\right)\\&=\dfrac{mv_{0}^{2}}{l}+Q\left\{-3E+B\sqrt{v_{0}^{2}-\dfrac{2QEl}{m}}\right\}}$(答)

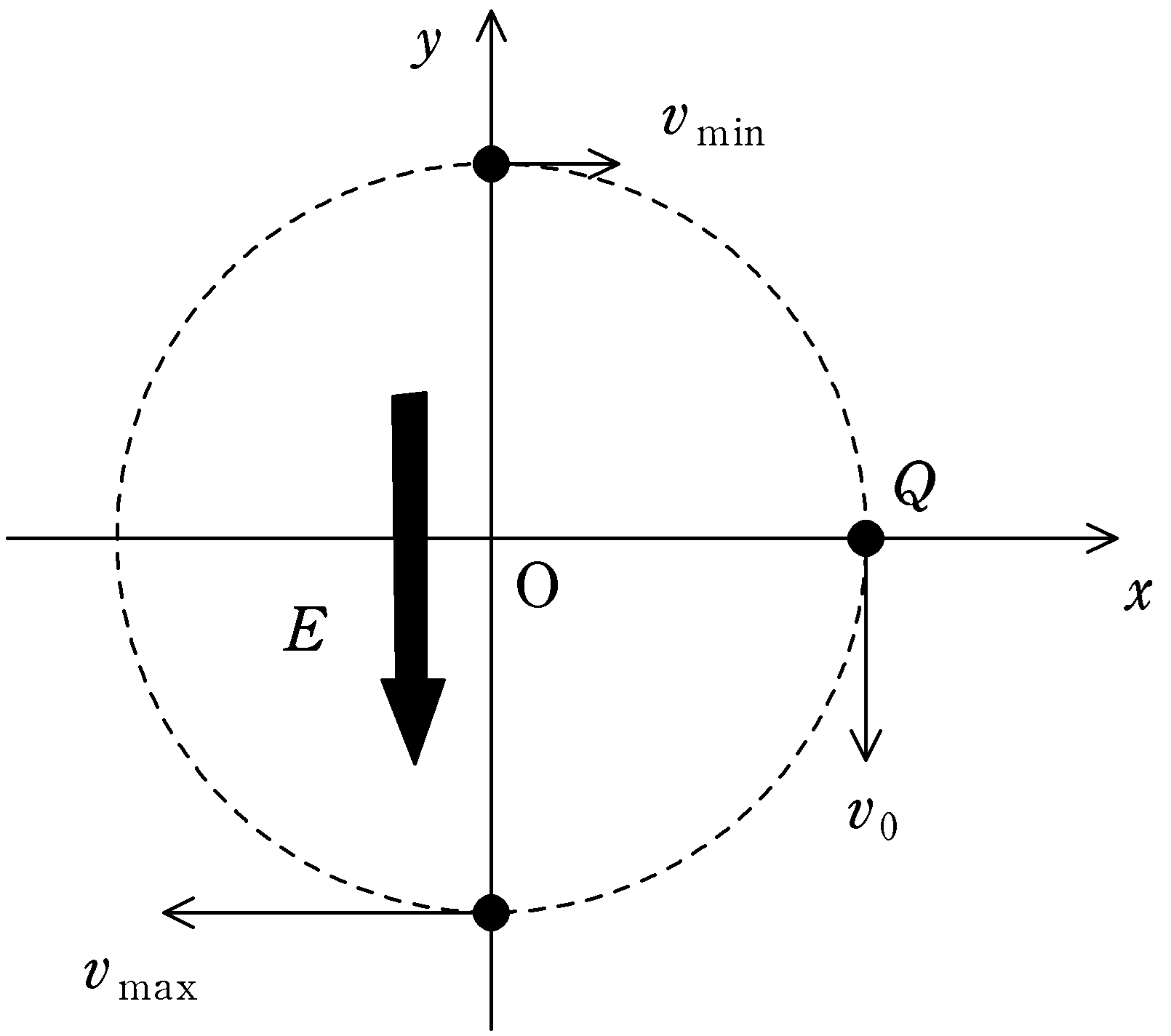

コメント