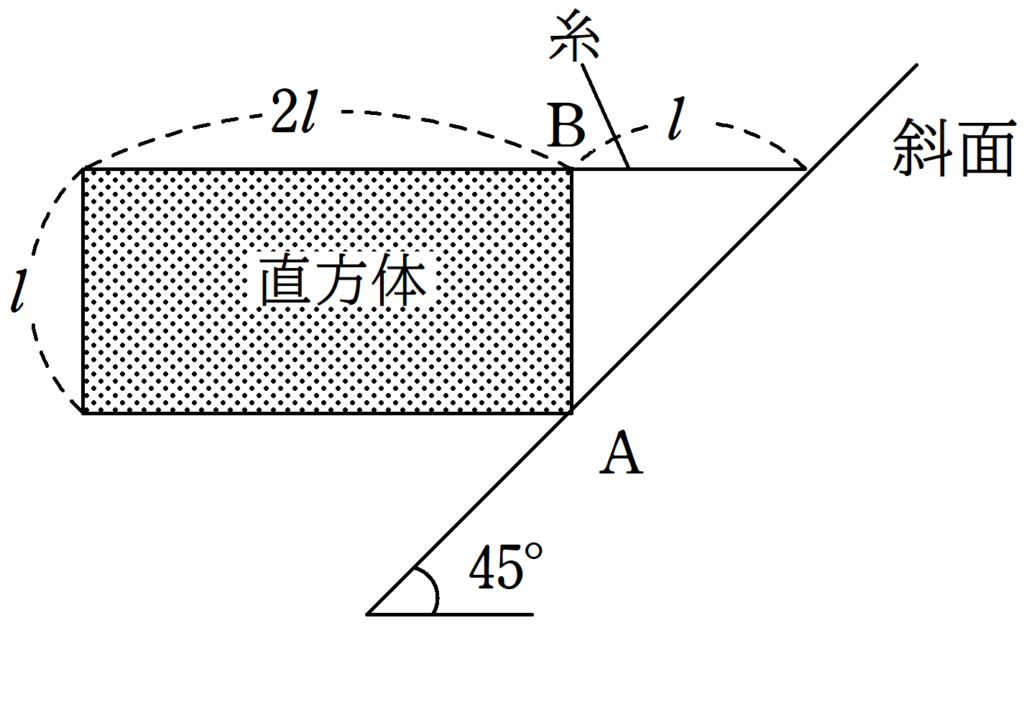
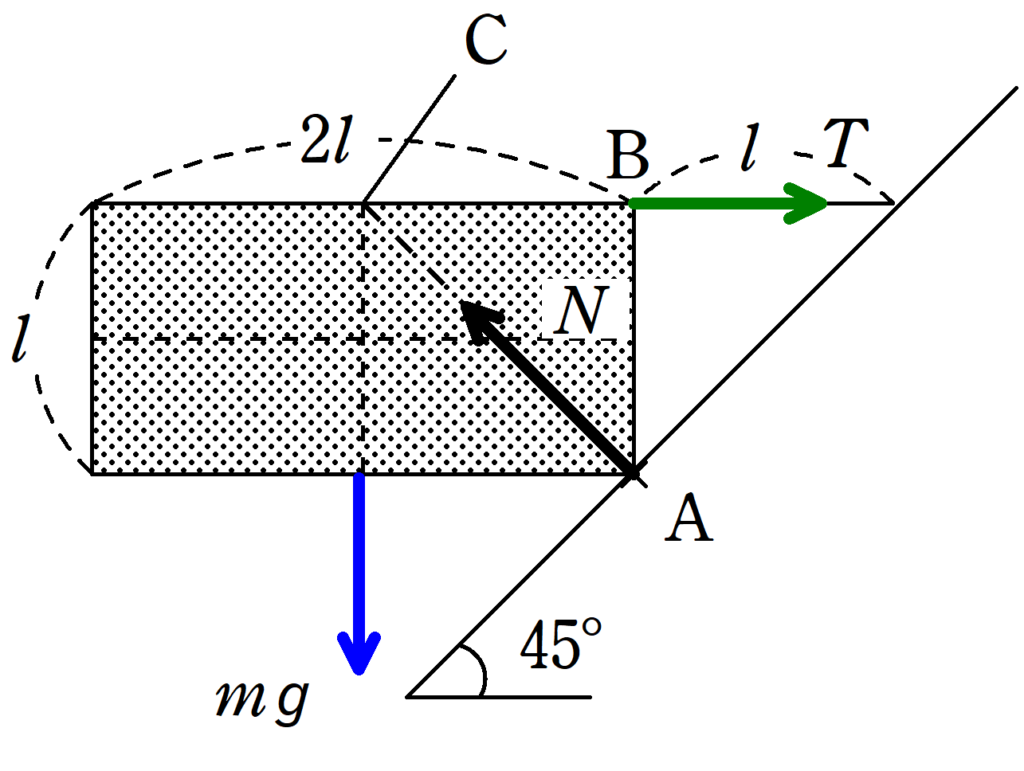
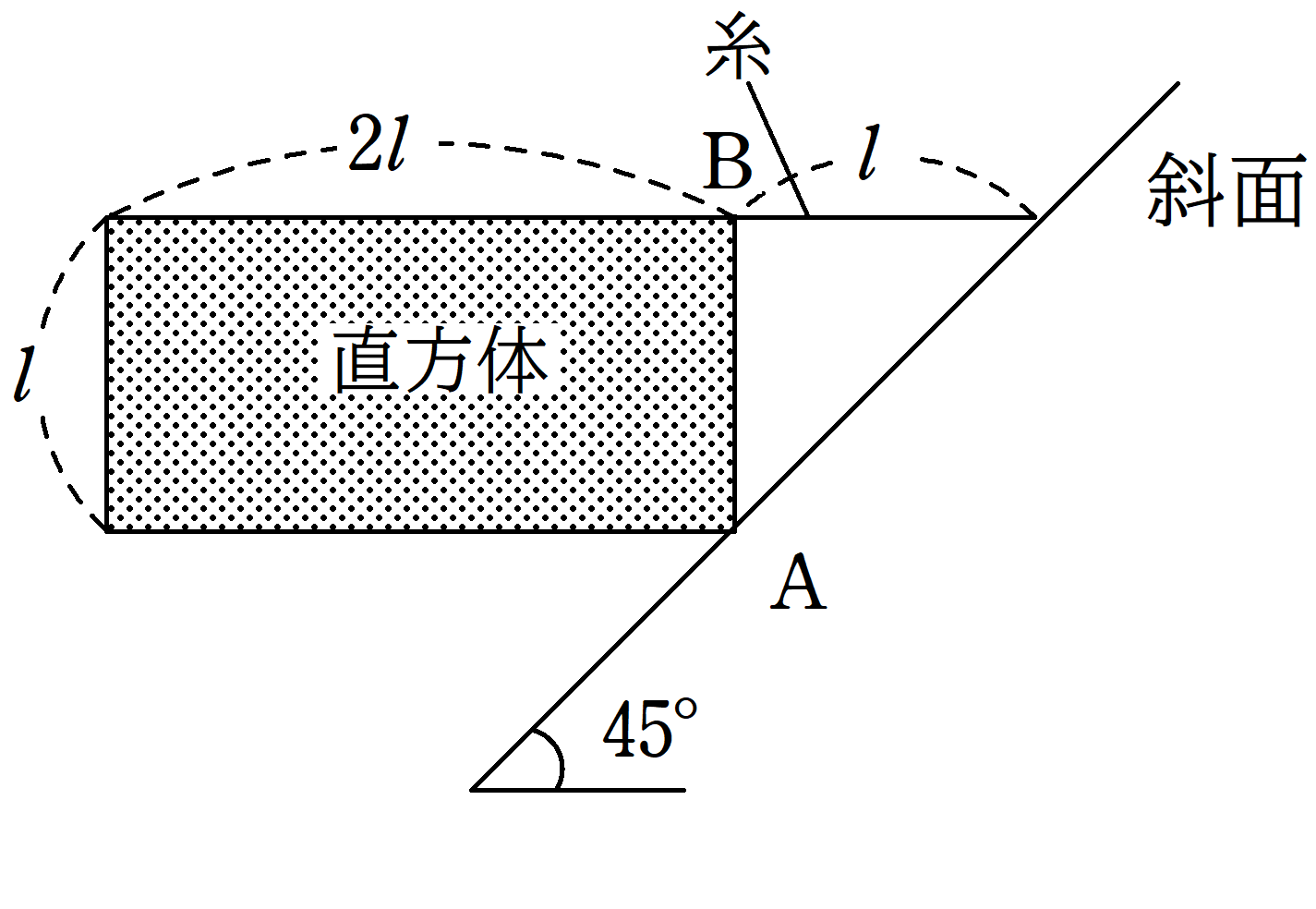
図のような傾角が$45^{\circ}$の斜面に縦の長さが$l$,横の長さが$2l$の直方体が点$\rm A$にて接して,点$\rm B$において糸でつながれている.糸は軽く,水平を向いている.直方体の密度は一様であり,質量は$m$である.重力加速度の大きさを$g$として,次の問いに答えよ.
(1) 点$\rm A$にはたらく抗力の大きさを$N$,点$\rm B$にはたらく張力の大きさを$T$とする.このとき,直方体の水平方向と鉛直方向のつり合いの式を立てることで,$N$と$T$をそれぞれ$m$,$g$を用いて表せ.
(2) 直方体の点$\rm A$まわりの力のモーメントのつり合いの式を立てることで,$T$を$m$,$g$で表し,(1)の答えと一致することを確かめよ.
<解答>
(1)
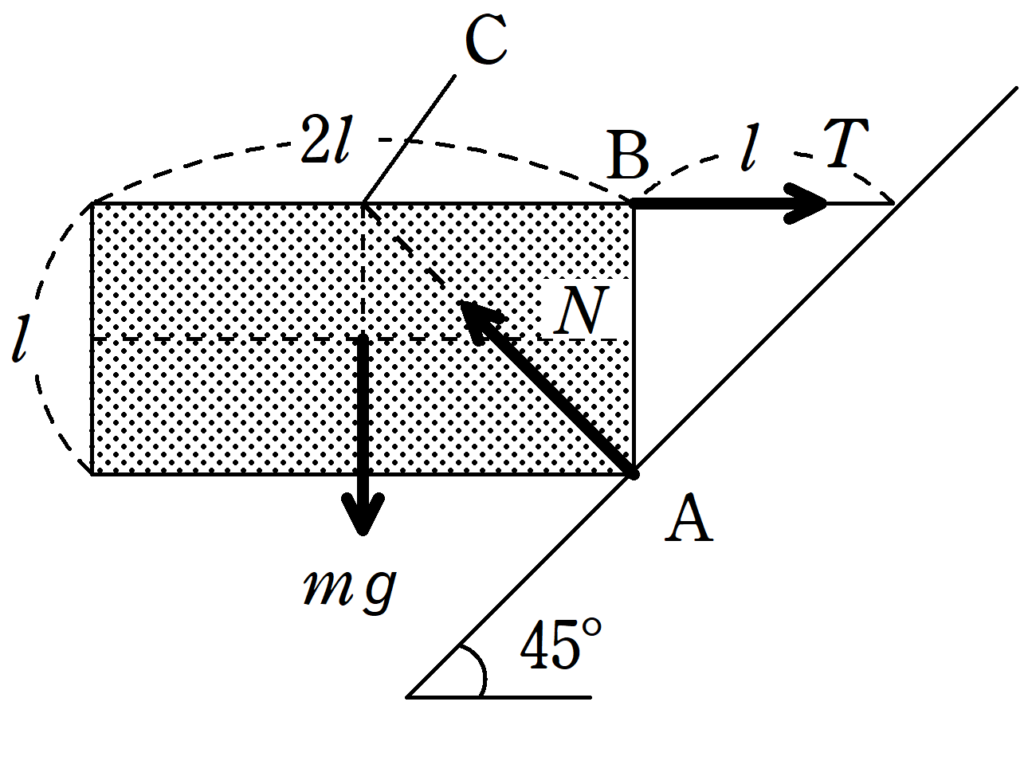

重力と張力の作用線は上図の$\rm C$で交わります.
したがって,$\rm A$にはたらく抗力は$\rm C$に向きます.
するとたまたま$\rm A$には摩擦力がはたらかない(斜面に平行な成分がない)ことがわかります.
垂直抗力を水平成分と鉛直成分にわけるとそれぞれの大きさはともに$\dfrac{N}{\sqrt{2}}$となります.
★ 水平方向のつり合いの式
$T=\dfrac{N}{\sqrt{2}}$ $\dots (\ast)$
★ 鉛直方向のつり合いの式
$\dfrac{N}{\sqrt{2}}=mg$ $\dots (2\ast)$
$(\ast)$,$(2\ast)$より
$T=mg$(答),$N=\sqrt{2}mg$ (答)
(2)
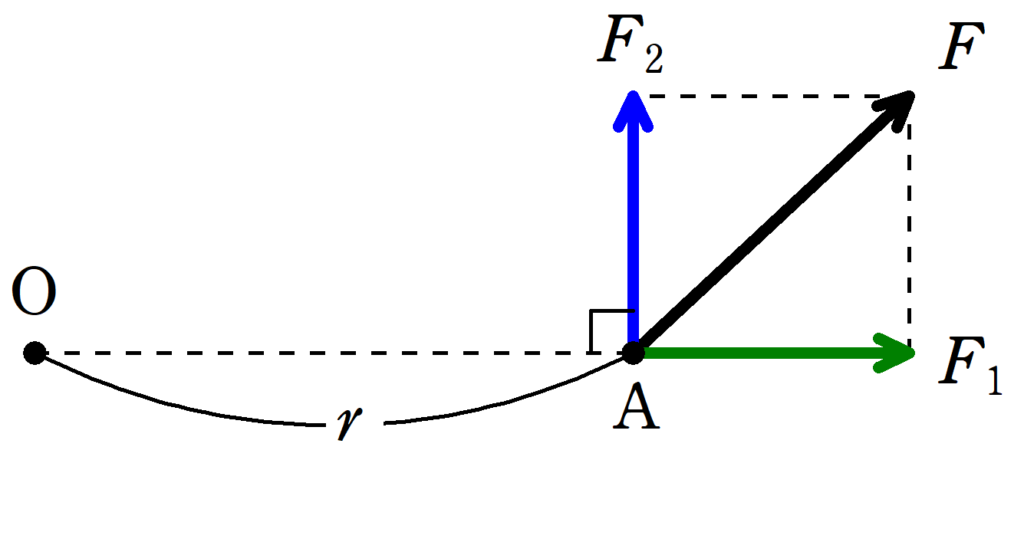
中心$\rm O$から距離$r$の点$\rm A$を始点とした大きさ$F$の力がはたらいている.この力の$\rm OA$方向の成分を$F_{1}$,$\rm OA$に垂直な成分を$F_{2}$とすると,力$F$の点$\rm O$まわりの力のモーメントの大きさ$N$は
$N=rF_{2}$
中心を$\rm O$とし,ある始点にはたらく力のモーメントを計算するとき,力の作用線上のどこに移動させても力のモーメントは同じである.
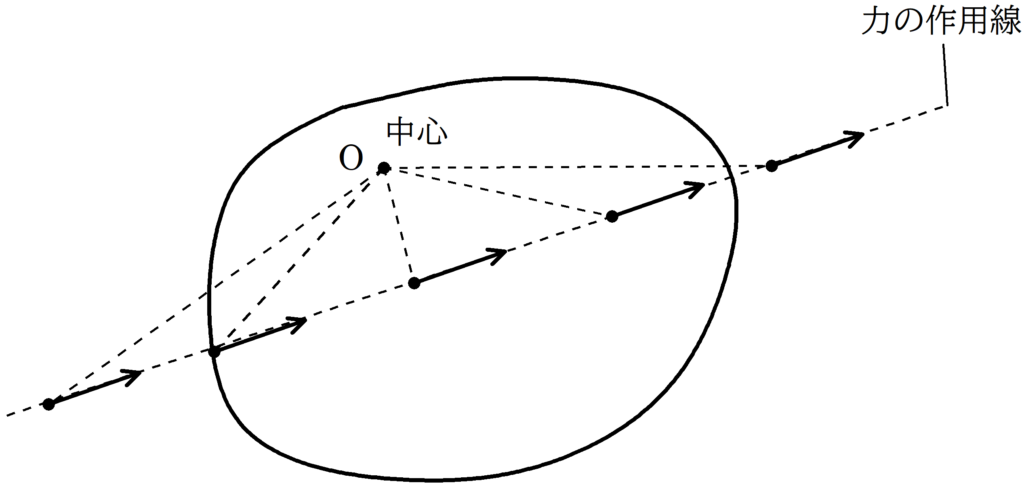

作用線平行移動の原理を使って,$\rm A$まわりの力のモーメントの式を立てましょう.

$\rm A$から$mg$の作用線までの距離は$l$.
$\rm A$から張力の作用線までの距離も$l$です.
★ $\rm A$まわりの力のモーメントのつり合いの式
$l\cdot T=l\cdot mg$
$\therefore T=mg$ (答)


コメント