
前回の内容はこちらです.
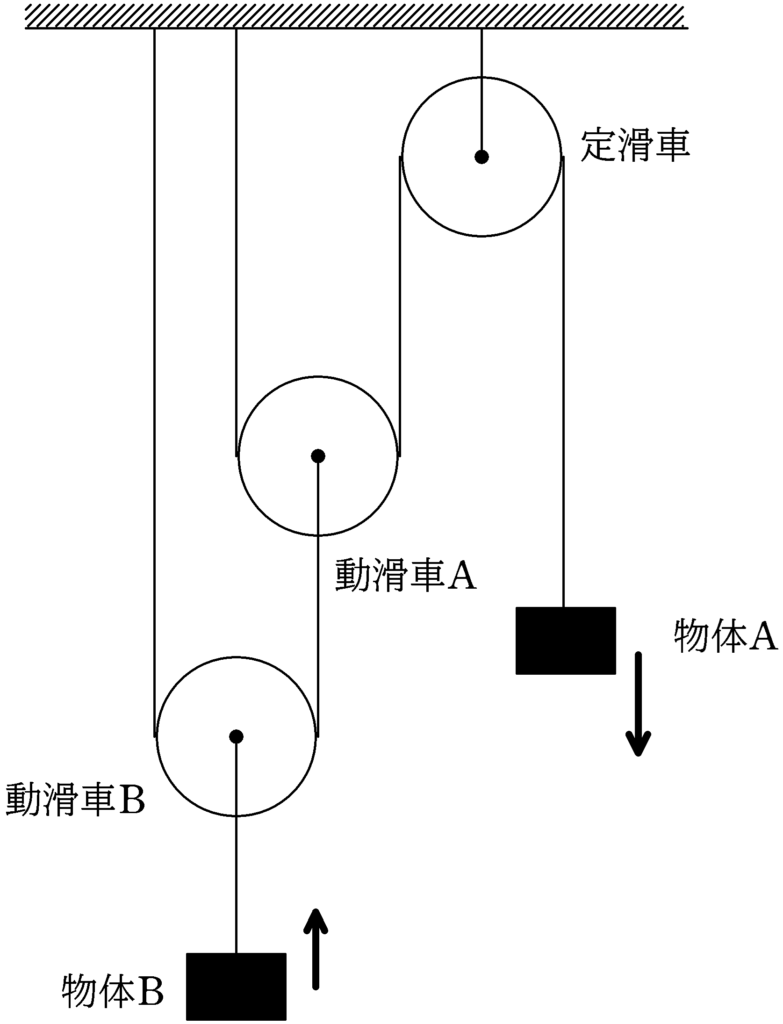
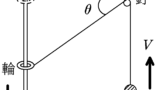
図のように,質量が無視でき,なめらかに回転できる定滑車と動滑車A,Bがある.
物体Aには軽くて伸び縮みしない糸がつながれており,糸は定滑車を介して動滑車Aにかけられており,天井につながっている.動滑車Bには,片側が天井に固定された軽くて伸び縮みをしない糸がかけられており,動滑車Aに固定されている.また,物体Bは動滑車Bに固定した糸によって垂れ下がっている.物体Aが鉛直下向きに運動し,物体Bが鉛直上向きに運動している際に,糸の長さが一定であることを利用して,物体Aと物体Bの加速度の大きさの比を答えよ.
<解答>

まずは,物体Aの加速度と動滑車Aの加速度の大きさの比から求めましょう.
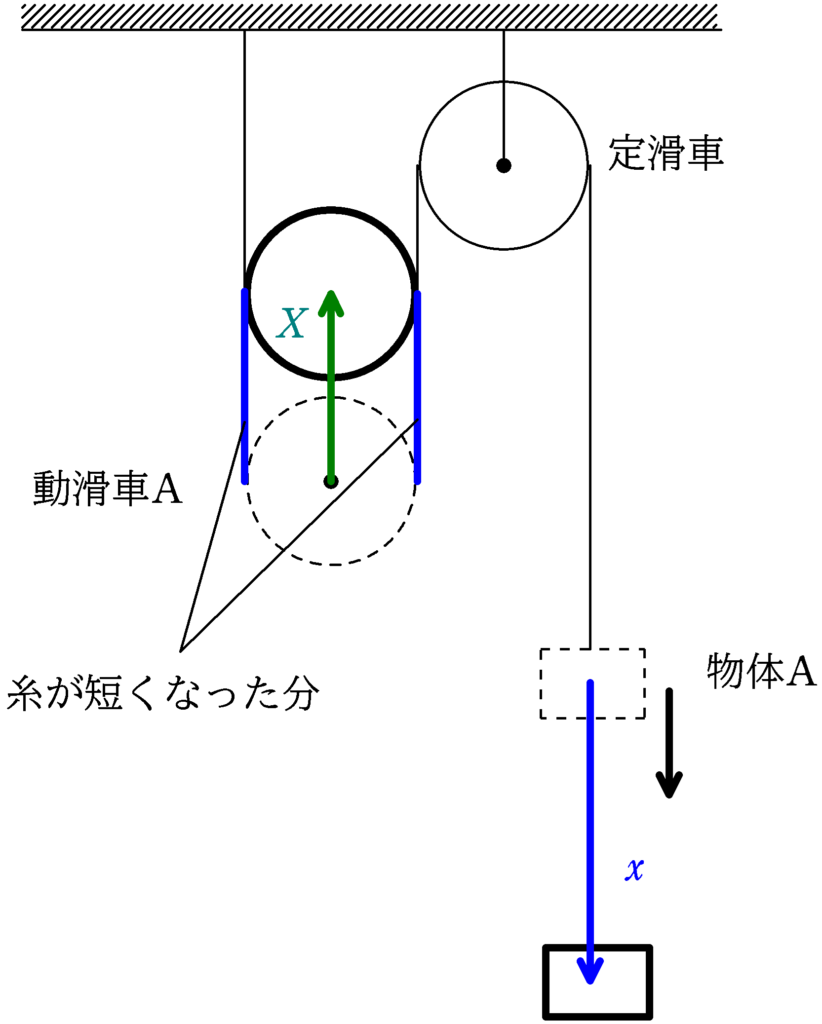

物体Aが下向きに$x$移動したとき,動滑車Aが上向きに$X$だけ移動したとしましょう.
動滑車Aが上向きに$X$だけ移動すると,上図のように,$2X$分だけ糸が短くなっています.
糸の長さが一定なので,物体Aが$x$だけ下に移動した距離と動滑車が$X$だけ移動したことで$2X$分だけ糸が短くなった距離は等しくなります.
つまり,
$x=2X$
この関係は瞬間々々成り立つので,時間$\varDelta t$の間に,物体Aが$\varDelta x$,動滑車Aが$\varDelta X$移動するとして
$\dfrac{\varDelta x}{\varDelta t}=2\dfrac{\varDelta X}{\varDelta t}$
となります.$v$を物体Aの速さ,$V_{\rm X}$を動滑車の速さとすると
$v=2V_{\rm X}$
の関係が成り立ちます.
同じように,$\varDelta t$の間に$\varDelta v$,$\varDelta V_{\rm X}$変化するとすれば
$\dfrac{\varDelta v}{\varDelta t}=2\dfrac{\varDelta V_{\rm X}}{\varDelta t}$
$a$を物体Aの加速度の大きさ,$A_{\rm X}$を動滑車Aの加速度の大きさとすると
$a=2A_{\rm X}$ $\dots (\ast)$
となります.
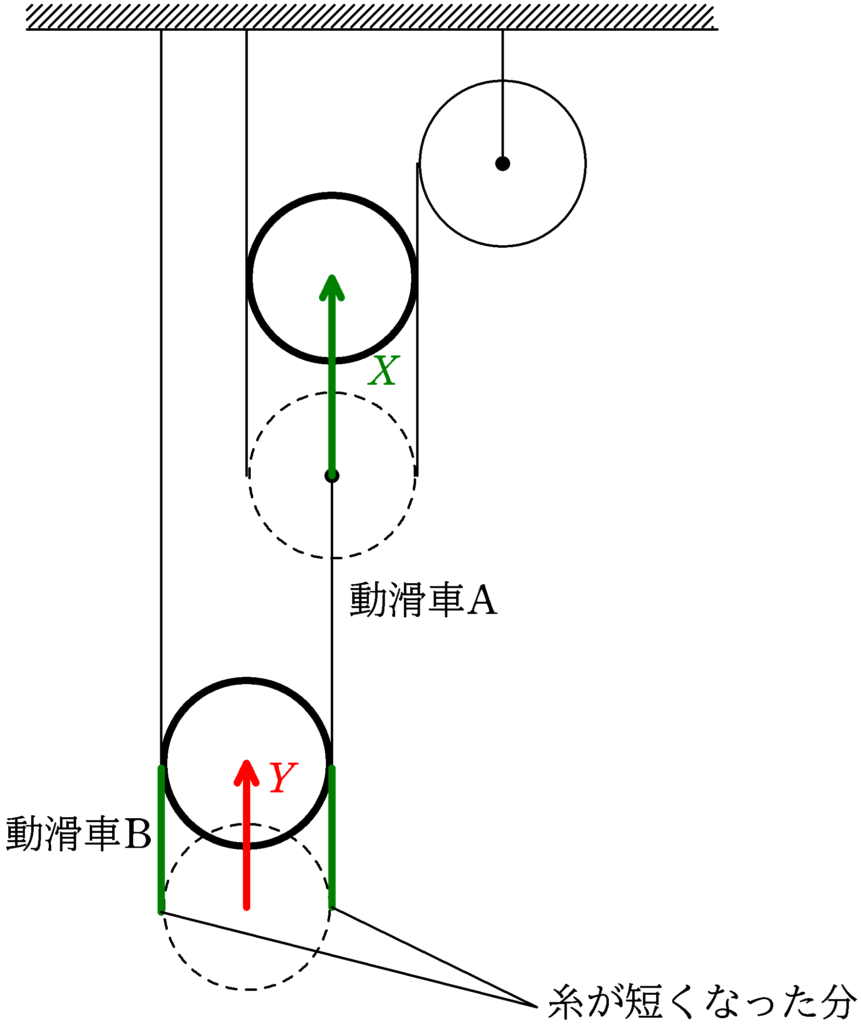

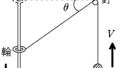
今度は,動滑車Aと動滑車Bの加速度の大きさの比を考えます.
動滑車Aが$X$だけ移動するとき,動滑車Bが$Y$だけ移動したとしましょう.
上図のように,動滑車Bが$Y$だけ移動すると$2Y$だけ(上図の2本の緑部分)糸が短くなるので,
$X=2Y$
の関係が成り立ちます.
動滑車Aと動滑車Bの加速度の大きさをそれぞれ$A_{\rm X}$,$A_{\rm B}$として物体Aと動滑車Aの加速度の大きさの比を求めたときと同じように考えると
$A_{\rm X}=2A_{\rm Y}$ $\dots (2\ast)$
となります.
$(\ast)$,$(2\ast)$より
$a=4A_{\rm Y}$

したがって,動滑車Bと物体Bの加速度の大きさは同じなので,
物体Aと物体Bの加速度の大きさの比は
$4:1$ (答)
となります.

コメント