twitterの問題5の解答

<解答>

面積速度一定の法則

$\rm O$を中心として物体が運動しているときを考える．

物体の軌道面と平行な力が中心$\rm O$（または中心軸）を向くとき，面積速度$\dfrac{\Delta S}{\Delta t}$が一定となる．

面積速度は中心$\rm O$と物体を結ぶ線分が単位時間あたりに通過する面積である．

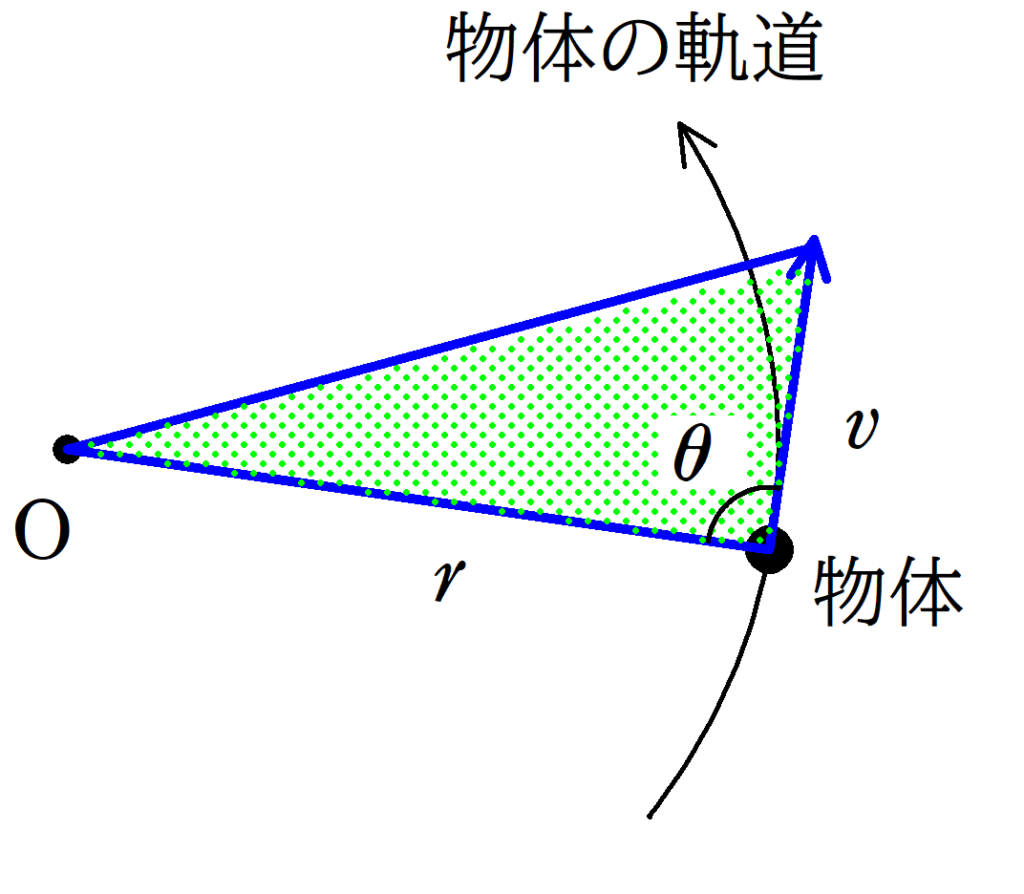
上図のように，$\rm O$と物体の距離が$r$，物体の速さを$v$，$\rm O$と物体を結ぶ線分と速度とのなす角を$\theta$とすると，面積速度は

$\dfrac{\Delta S}{\Delta t}=\dfrac{1}{2}rv\sin\theta$

面積速度$\times$微小時間$=$微小時間に通過した面積

より，

面積速度$\times $周期$=$1周して通過した面積の和

人口衛星が1周すると円の面積$\pi r^{2}$分通過するので

$A\times T=\pi r^{2}$　$\therefore\,\, T=$$\dfrac{\pi r^{2}}{A}$

※　ちなみに人工衛星の速さを$v$とすると，面積速度は$A=\dfrac{1}{2}rv$となり，上式の右辺に代入すると

$\dfrac{\pi r^{2}}{\dfrac{1}{2}rv}=\dfrac{2\pi r}{v}$

となり，確かに等速円運動の周期の式になっています．