
PHYさん
前回の内容はこちらです.
また,今回の問題は別な解き方として,こちらでも紹介しています.
問題
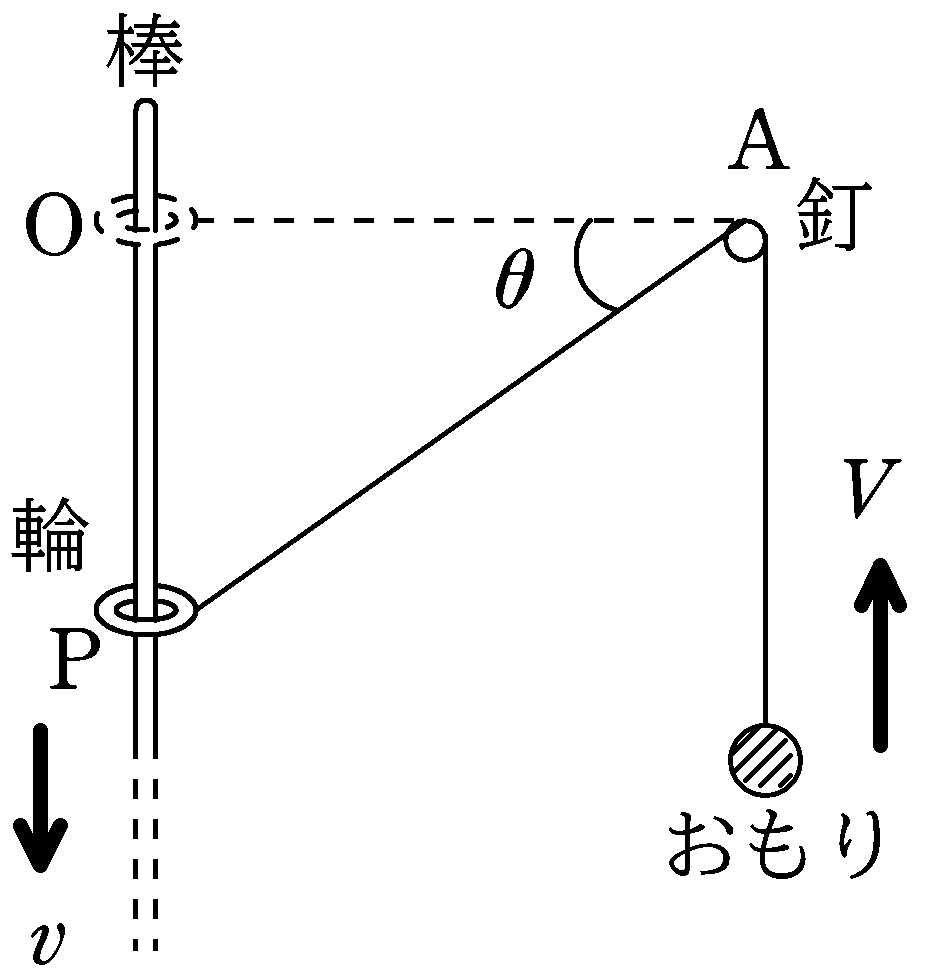
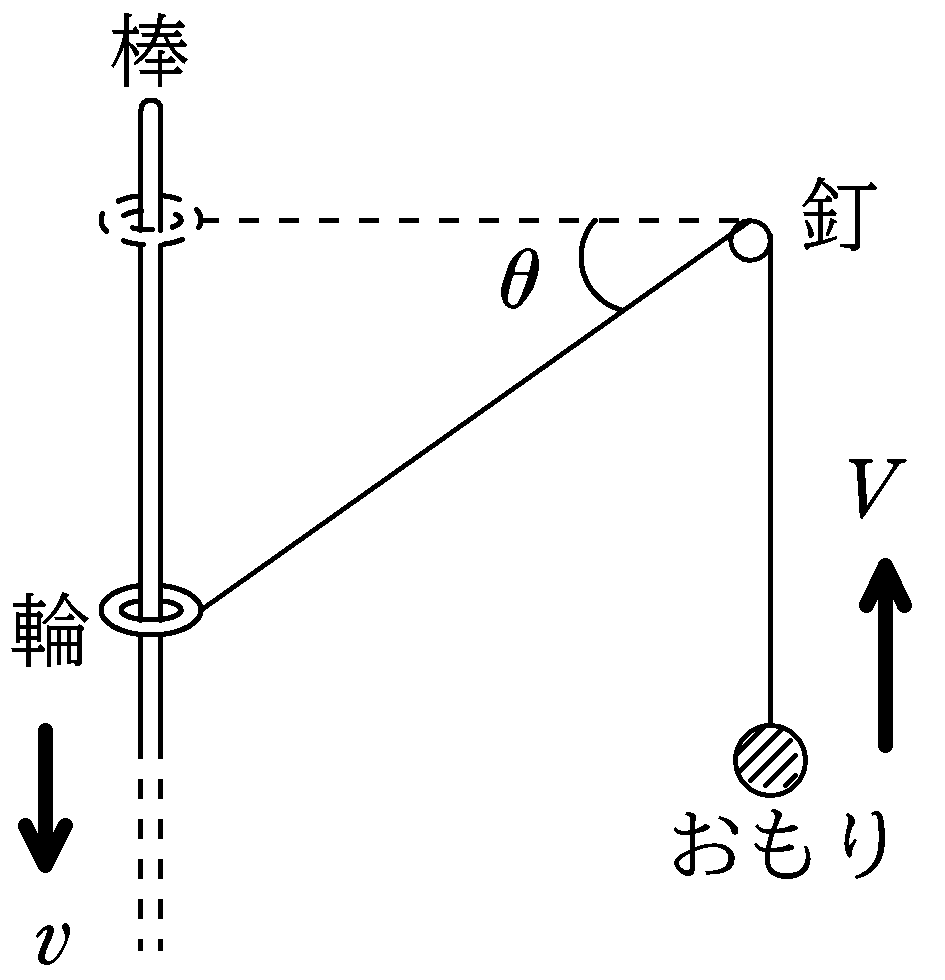
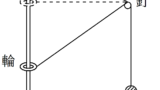
図のように,鉛直に立てた棒に質量$m$の輪を通し,輪に軽い糸をつけて,糸を棒から距離$l$だけ離れた釘(この位置をAとする.)にかけ,糸の先端に質量$M(>m)$のおもりをつけて鉛直に垂らしてある.糸と釘はなめらかであり,輪の位置は最初釘と同じ高さにあった状態(このときの輪の位置をOとする.)から静かに手をはなした.
ある時刻における輪の位置をPとすると,$\angle{\rm OAP=\theta}$であった.このときの輪の速さを$v$,おもりの速さを$V$とする.糸の長さが一定である束縛条件から,$v , V , \theta$の間に成り立つ関係式を求めよ.

NEKO
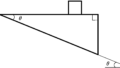
糸の長さが一定である条件を使いたいので,糸の長さ方向(下図$X$の方向)の速度を考えてみましょう.
この際,おもりの向きを便宜的に糸が一直線になるように移動させて考えるといいね.
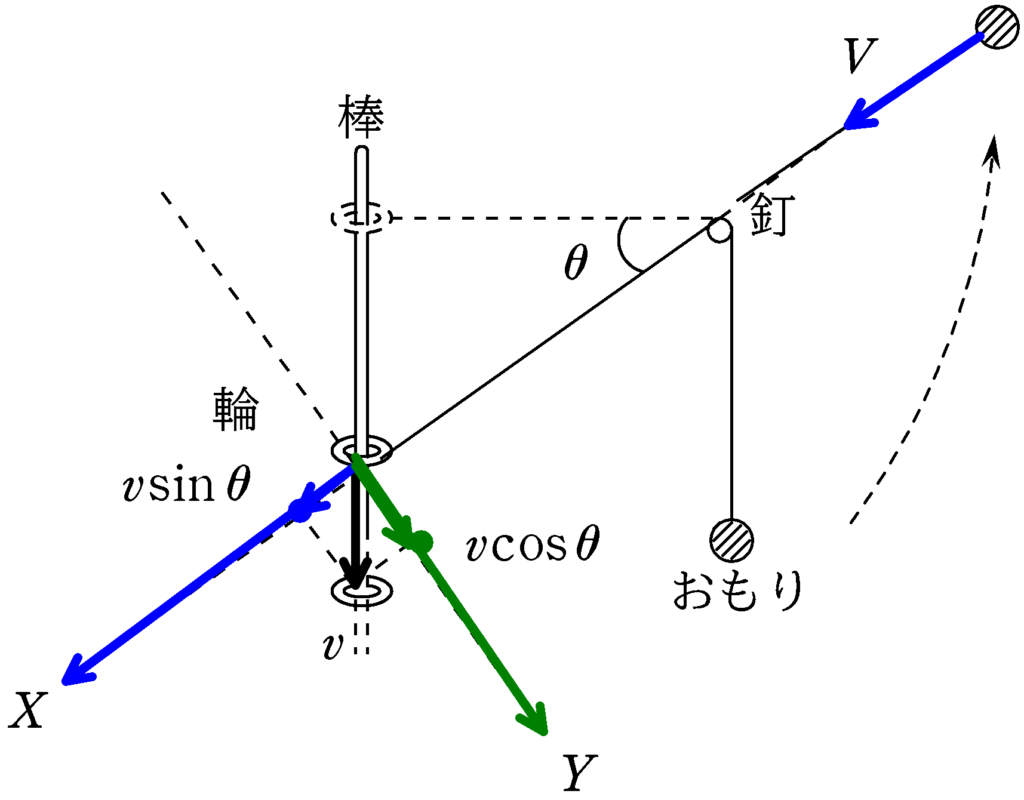
輪は鉛直下向きに移動してるけど,下図のように,$X$と$Y$方向に移動しているとも考えることができるね.

NEKO
おもりの$X$の方向の速度成分は$v\sin\theta$で,おもりの$X$成分は$V$です.糸の長さ一定だからこの速度が同じであるという条件を考えることができるね.
したがって,
$v\sin\theta=V$ (答)

コメント
[…] […]