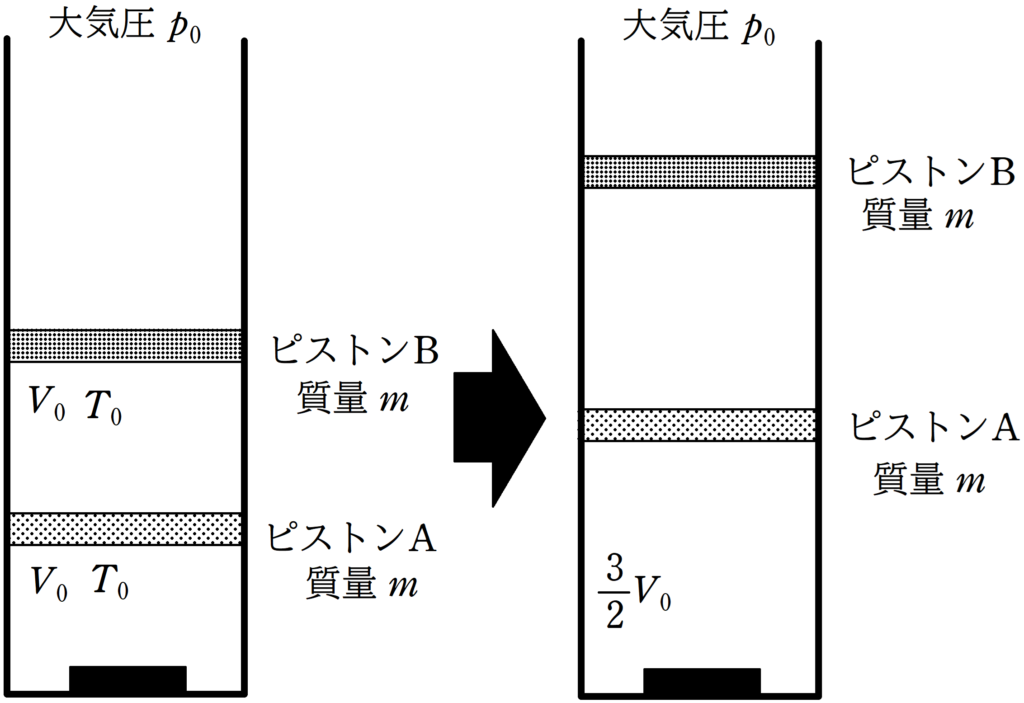
上図のように,鉛直に固定された断熱容器があり,質量$m$で断面積$S$のピストンA,Bによって単原子分子理想気体が封入されている.
ピストンAと容器によって封入されている気体を”下側の気体“,容器とピストンAとピストンBによって封入されている気体を”上側の気体”名づける.
ピストンA,Bはともになめらかに動くことができ,ピストンAは熱をよく通すが,ピストンBは熱を通さない.
大気圧は$p_{0}$であり,変化しないものとする.
はじめ,下側の気体と上側の気体はともに体積が$V_{0}$,絶対温度が$T_{0}$であった.
この状態から,断熱容器の底部に温度調節器を設置し,気体Aをゆっくりとあたためると,ピストンAとピストンBはゆっくりと上昇し,下側の気体の体積が$\dfrac{3}{2}V_{0}$になったところで,温度調節器をとめた.
このとき,次の問いに答えよ.
(1) 温度調節器であたため終わった後の下側の気体の圧力,絶対温度,上側の気体の圧力,絶対温度,体積をそれぞれ求めよ.
(2) 気体をあたためはじめてから,温度調節器を止めるまでに,上側の気体がピストンBにする仕事を求めよ.
<解答>
(1)

熱力学の問題で意識をして立てて欲しいのは,次の3つの式です.
- 可動部分のつり合いの式 → 力の情報が出てくる
- 理想気体の状態方程式(ボイルシャルルの法則)
- 熱力学第一法則 → エネルギーの情報が出てくる

まずは,可動部分のつり合いの式を立ててみましょう.
下側の気体の圧力を$p_{\rm A}$,上側気体の圧力を$p_{\rm B}$としましょう.
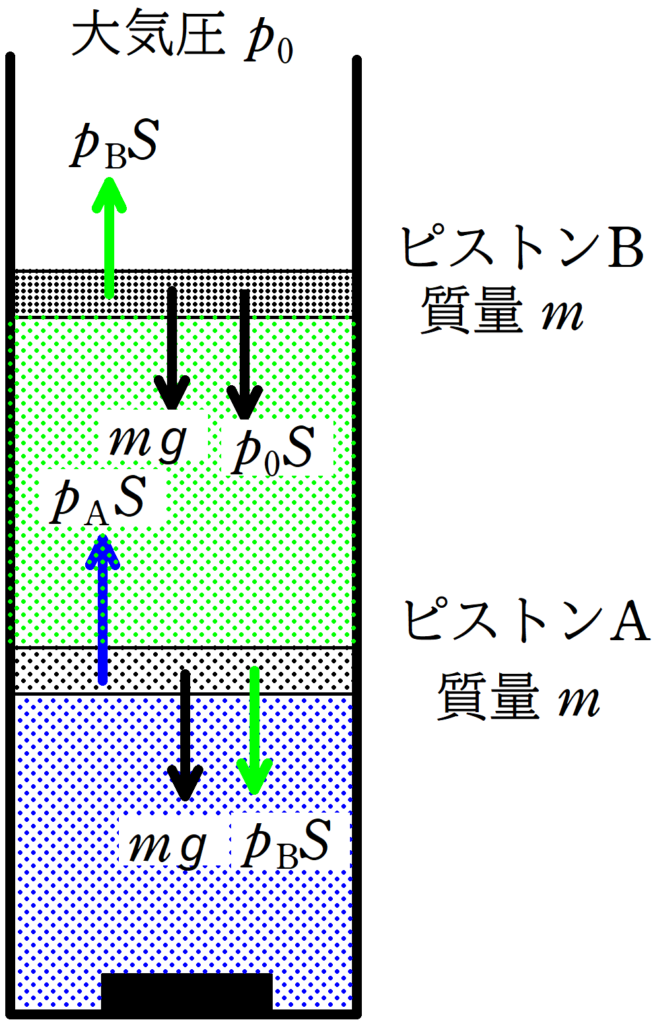

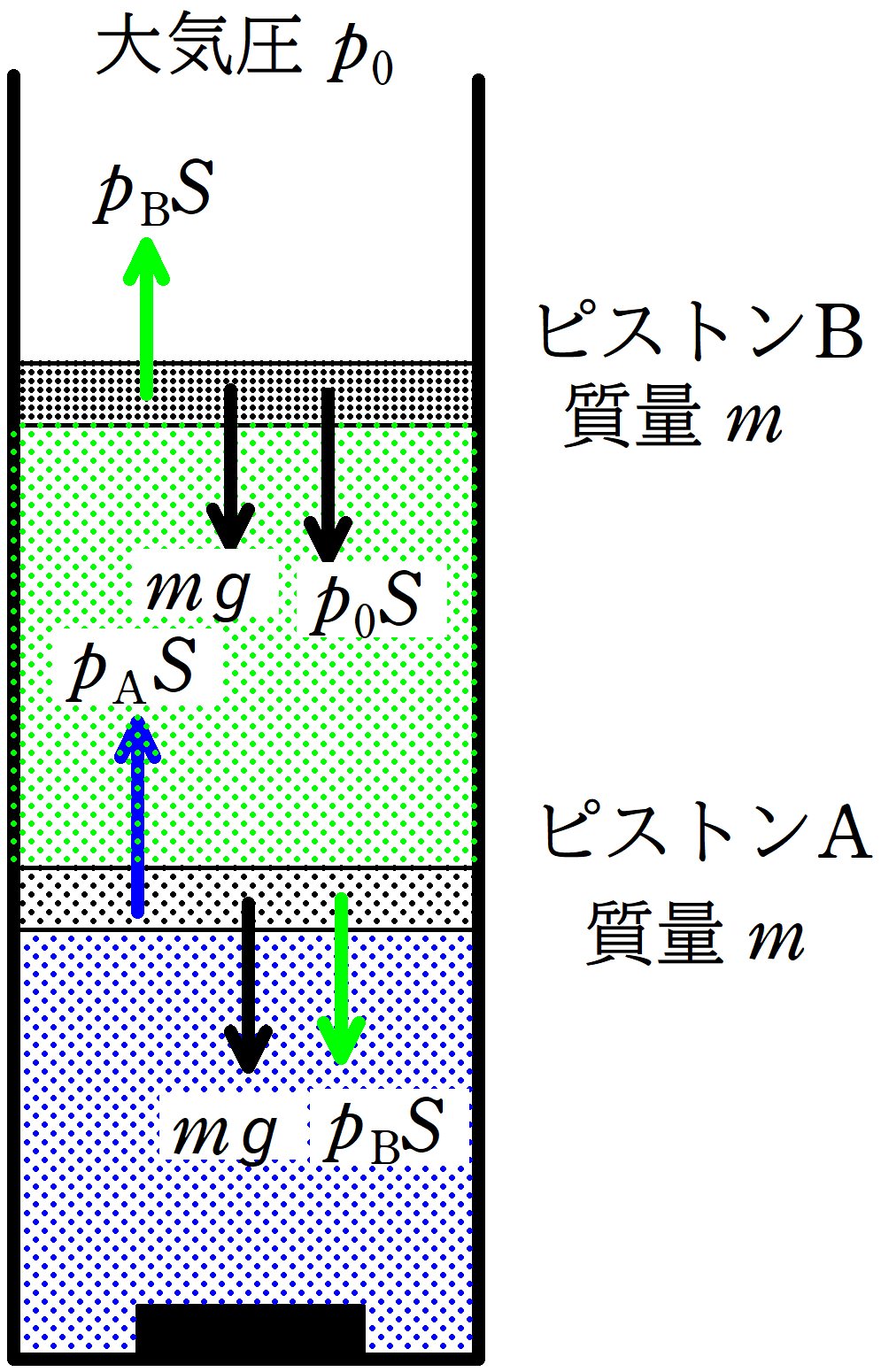
ピストンAにはたらく力は次の3つだよ.
・上側気体がピストンAを押す力$p_{\rm B}S$
・下側気体がピストンAを押す力$p_{\rm A}S$
・ピストンAの重力$mg$
そして,ピストンBにはたらく力は,次の3つです.
・上側気体がピストンBを押す力$p_{\rm B}S$
・容器外の空気がピストンBを押す力$p_{0}S$
・ピストンBの重力$mg$
★ ピストンAのつり合いの式
$p_{\rm A}S=p_{\rm B}S+mg$ $\dots (\ast)$
★ ピストンBのつり合いの式
$p_{\rm B}S=p_{0}S+mg$
$\therefore$ $p_{B}=p_{0}+\dfrac{mg}{S}$ $\dots (2\ast)$
$(2\ast)$を$(\ast)$に代入して
$\eqalign{p_{\rm A}&=p_{\rm B}+\dfrac{mg}{S}\\&=p_{0}+\dfrac{mg}{S}+\dfrac{mg}{S}\\&=p_{0}+\dfrac{2mg}{S}}$

$p_{\rm A}=p_{0}+\dfrac{2mg}{S}$と$p_{\rm B}=p_{0}+\dfrac{mg}{S}$の結果をみると,下側の気体と上側の気体の圧力は大気圧とピストンの重力で決まっていることが確認できるね.
だから,気体があたためられても,気体の圧力は変化しないよ.
つまり,定圧変化をします.
気体の圧力は可動部分のつり合いから外部の力の情報の変化を読みとればいいんです.
では,次に体積や絶対温度の変化を考えてみましょう.

ボイル・シャルルの法則を立てることができますね.
理想気体について,物質量$n$が変化しないとき,気体の圧力を$p$,気体の体積を$V$,絶対温度を$T$とすると,
$\dfrac{pV}{T}=$一定
が成り立つ.(ボイル・シャルルの法則)
特に,温度が一定のとき
$pV=$一定(ボイルの法則)
圧力が一定のとき
$\dfrac{V}{T}=$一定(シャルルの法則)
が成り立つ.
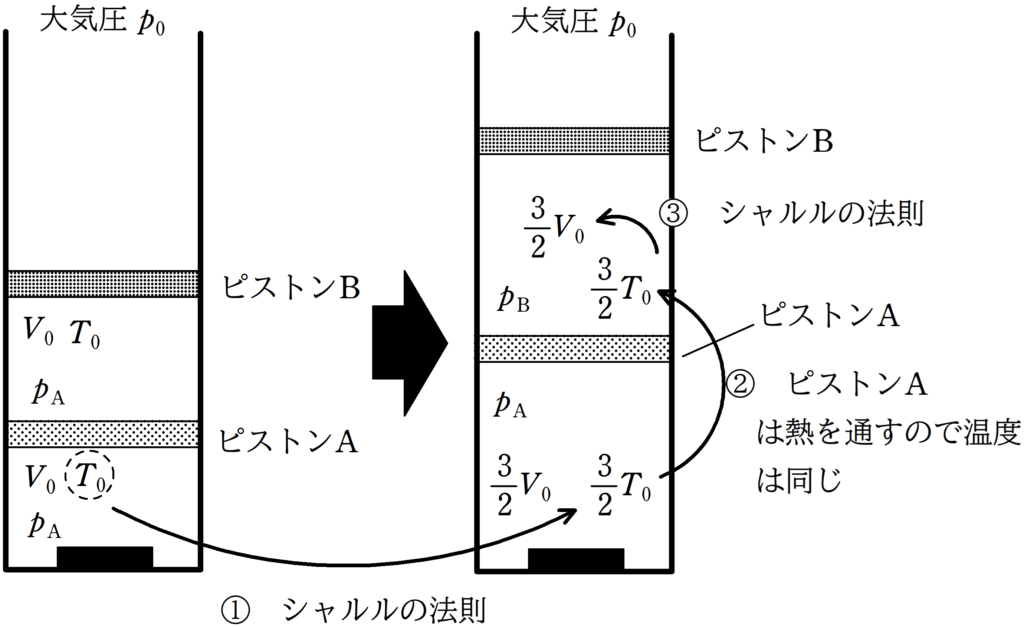
★ ①気体Aに関してのシャルルの法則
状態変化後の気体Aの絶対温度を$T_{\rm A}$として
$\dfrac{V_{0}}{T_{0}}=\dfrac{\dfrac{3}{2}V_{0}}{T_{\rm A}}$
$\therefore$ $T_{\rm A}=\dfrac{3}{2}T_{0}$
★ ②状態変化後について
①より,気体Aの絶対温度が$\dfrac{3}{2}T_{0}$.また,ピストンAは熱をよく通すので,状態変化後の気体Bの絶対温度$T_{\rm B}$も$T_{\rm B}=\dfrac{3}{2}T_{0}$となる.
★ ③気体Bについてのシャルルの法則
状態変化後の気体Bの体積を$V_{\rm B}$とすると,シャルルの法則より
$\dfrac{V_{0}}{T_{0}}=\dfrac{V_{\rm B}}{\dfrac{3}{2}T_{0}}$
$\therefore$ $V_{\rm B}=\dfrac{3}{2}V_{0}$
以上より,答えは
上側の気体の圧力 $p_{\rm B}=p_{0}+\dfrac{mg}{S}$
下側の気体の圧力 $p_{\rm A}=p_{0}+\dfrac{2mg}{S}$
上側気体の絶対温度 $T_{\rm B}=\dfrac{3}{2}T_{0}$
下側気体の絶対温度 $T_{\rm A}=\dfrac{3}{2}T_{0}$
上側気体の体積 $V_{\rm B}=\dfrac{3}{2}V_{0}$
(2)

次に,上側の気体がピストンBにする仕事$W_{\rm B}$を求めましょう.
でも,これって,定圧変化なんだし,
$\eqalign{W_{\rm B}&=p_{\rm B}\Delta V\\&=(p_{0}+\dfrac{mg}{S})(\dfrac{3}{2}V_{0}-V_{0})\\&=\dfrac{1}{2}(P_{0}+\dfrac{mg}{S})V_{0}}$
でおしまいなんじゃないかな??

いえ,それは間違いです.
いま,きかれているのは,
上側の気体がピストンBにする仕事
であって,
上側気体がピストンAとピストンBにする仕事
ではありません.

そっか!
さっきの計算では,上側の気体がピストンAにする負の仕事も含めてしまっているんだ!!
じゃあ,どうやって仕事を計算するの??

上側の気体がピストンBに及ぼす力が一定なので,
仕事=力×移動距離
でよいでしょう.

じゃあ,
体積($V$)=底面積($S$)×高さ($h$)
の式から
$h=\dfrac{V}{S}$
で高さを計算しておく必要があるね.
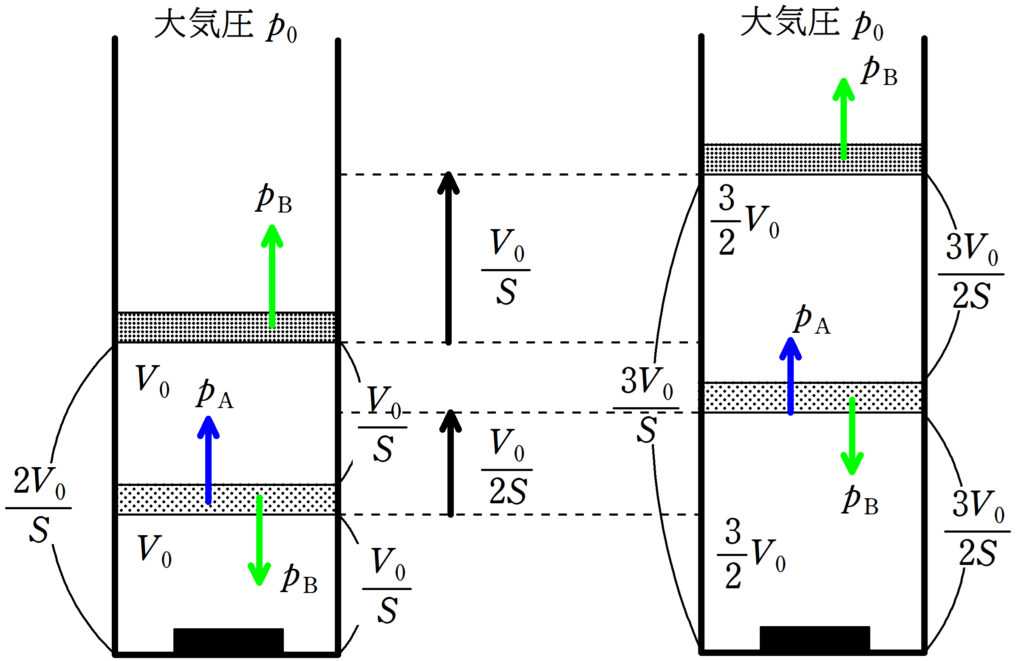

もともとのピストンBの高さは$\dfrac{2V_{0}}{S}$で,状態変化後のピストンの高さは$\dfrac{3V_{0}}{S}$になったんだから,ピストンBの移動距離$\Delta x$は
$\Delta x=\dfrac{3V_{0}}{S}-\dfrac{2V_{0}}{S}=\dfrac{V_{0}}{S}$
となるね.
★ 上側気体がピストンBにする仕事
$\eqalign{W_{\rm B}&=(p_{\rm B}S)\cdot \Delta x\\&=(p_{0}S+mg)\cdot \dfrac{V_{0}}{S}\\&=(p_{0}S+mg)\cdot \dfrac{V_{0}}{S}}$
答え $W_{\rm B}=(p_{0}S+mg)\cdot \dfrac{V_{0}}{S}$



コメント
[…] […]
[…] 2つのピストンが動くときに気体がする仕事[よく見かける間違い] […]