
前回の内容はこちらです.

熱気球では,まず
- 気球のつり合い
- ボイル・シャルルの法則(熱気球で使いやすい形に変形した$\dfrac{P}{\rho T}=一定$の式)
だったね.「2」の式は次のようになります.
理想気体の圧力を$P$,絶対温度を$T$,密度を$\rho$とする.このとき,理想気体の分子量が変化しなければ次の式が成り立つ.
$\dfrac{P}{\rho T}=$一定

また,熱気球のつり合いの式を立てる際は,浮力(まわりの空気からおされる力の和)を考えます.浮力の大きさは「アルキメデスの原理」で導出できるようにしましょう.
物体にはたらく浮力の大きさは,物体がおしのけた液体(または気体)の重さと等しい.
おしのけた液体(または気体)の密度を$\rho$,押しのけた分の物体の体積を$V$,重力加速度の大きさを$g$とすると,浮力の大きさ$F$は
$F=\rho Vg$
※ $\rho$は物体の密度ではなく,おしのけた液体(または気体)の密度である.

今回は地上にある熱気球ではなく,ある高さに浮上したときの問題です.
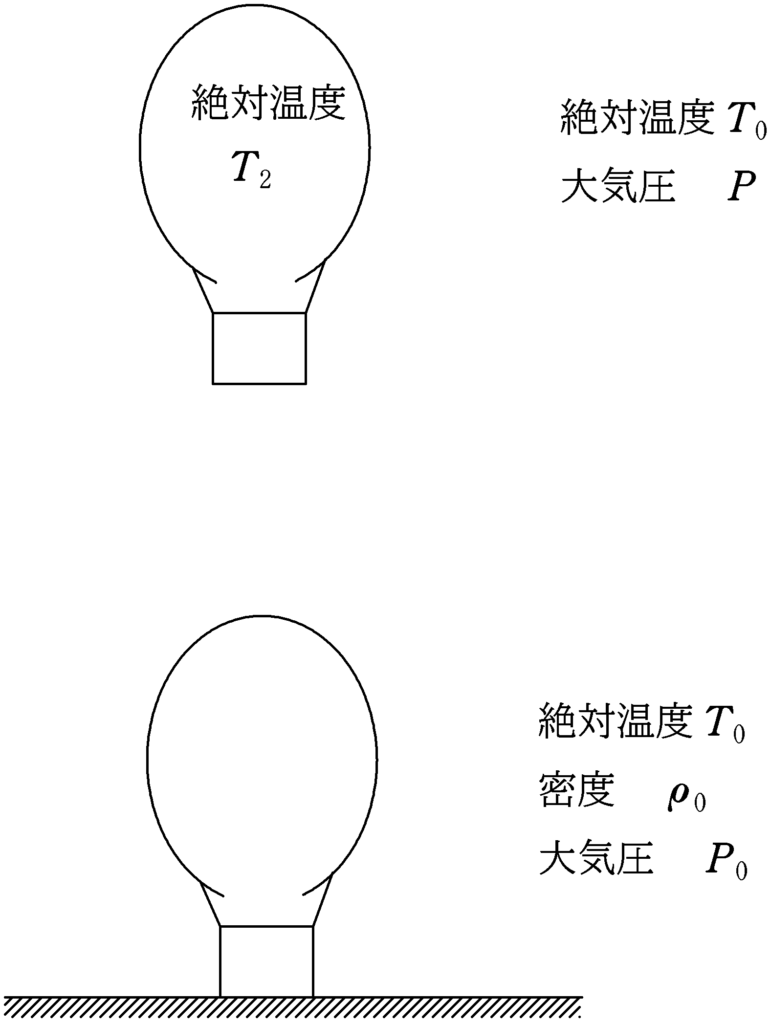
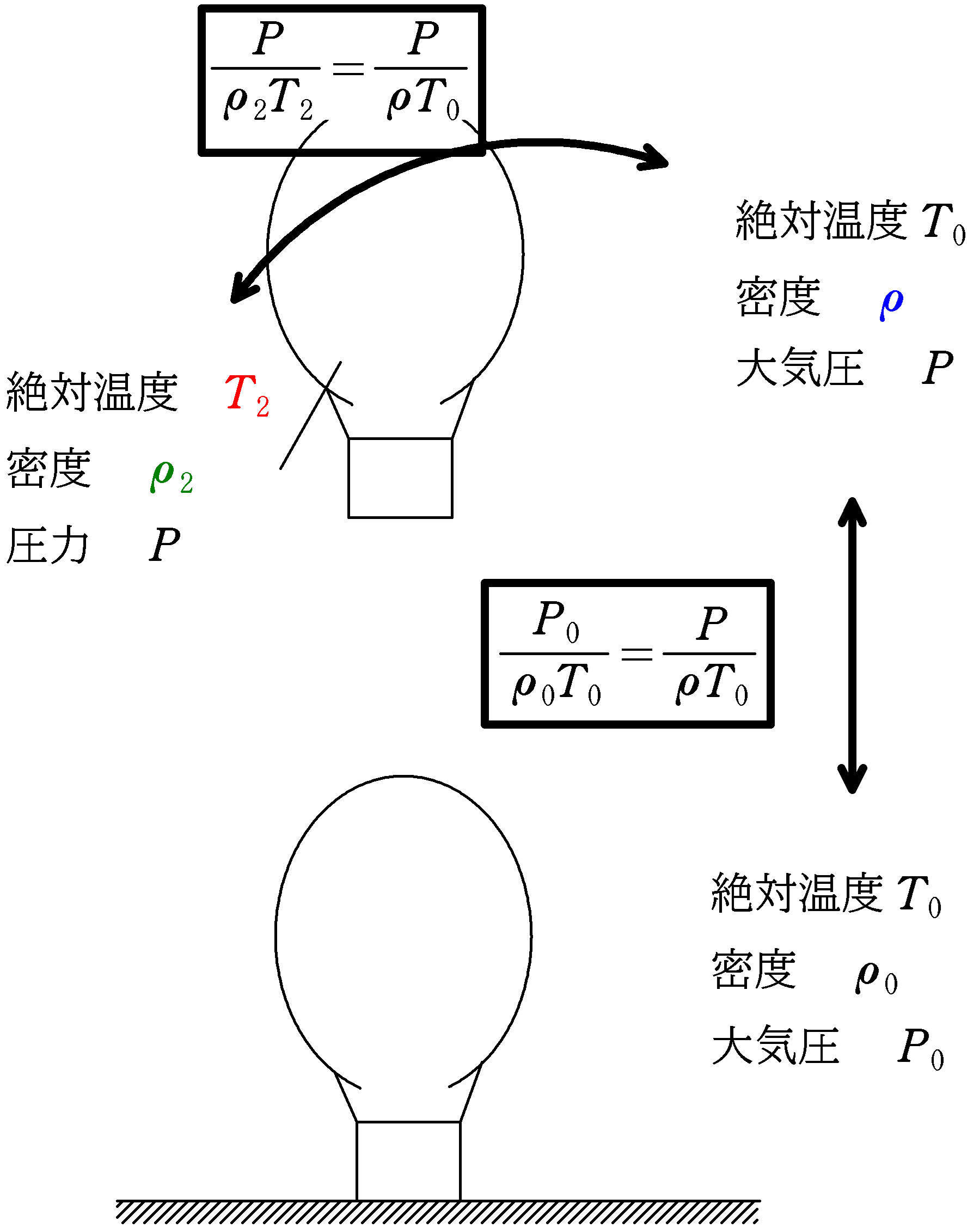
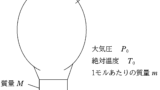
質量$M$の熱気球がある高さにて静止している.熱気球の空気を入れる部分の体積は$V$である.また,地上における空気の密度を$\rho_{0}$,絶対温度を$T_{0}$,大気圧を$P_{0}$とする.熱気球内の空気と地上における空気は自由に出入りできるようになっているため,気球内の圧力は大気の圧力と同じである.以下,空気は理想気体と考えることができる.また,重力加速度の大きさを$g$とする.熱気球が静止している場所における大気の絶対温度は地上と同じ$T_{0}$であり,大気圧は$P$である.このとき,熱気球内の気体の絶対温度$T_{2}$を$P,\rho_{0},T_{0},V,M$を用いて表せ.ただし,地上と熱気球がある場所の空気の分子量は変化しないものとする.
<解答>
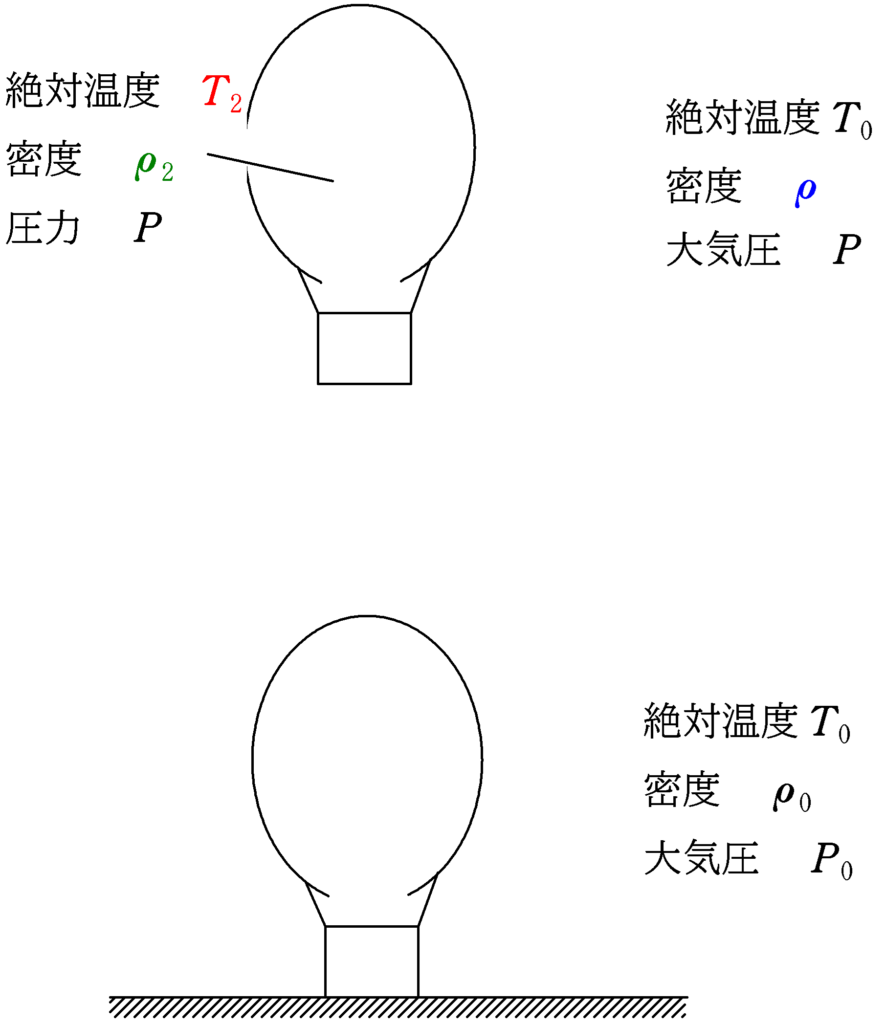

まず,問題文に与えられていないものとして,熱気球が静止している高さにある大気の密度と気球内の密度があります.それぞれ,$\rho$,$\rho_{2}$と設定しましょう.
その上で,気球のつり合いの式を立てます.
鉛直上方向に浮力$\rho Vg$(アルキメデスの原理によればおしのけた空気の重さに等しい),鉛直下方向に気球の重力$Mg$と気球内の気体の重さ$\rho_{2}Vg$がはたらきます.
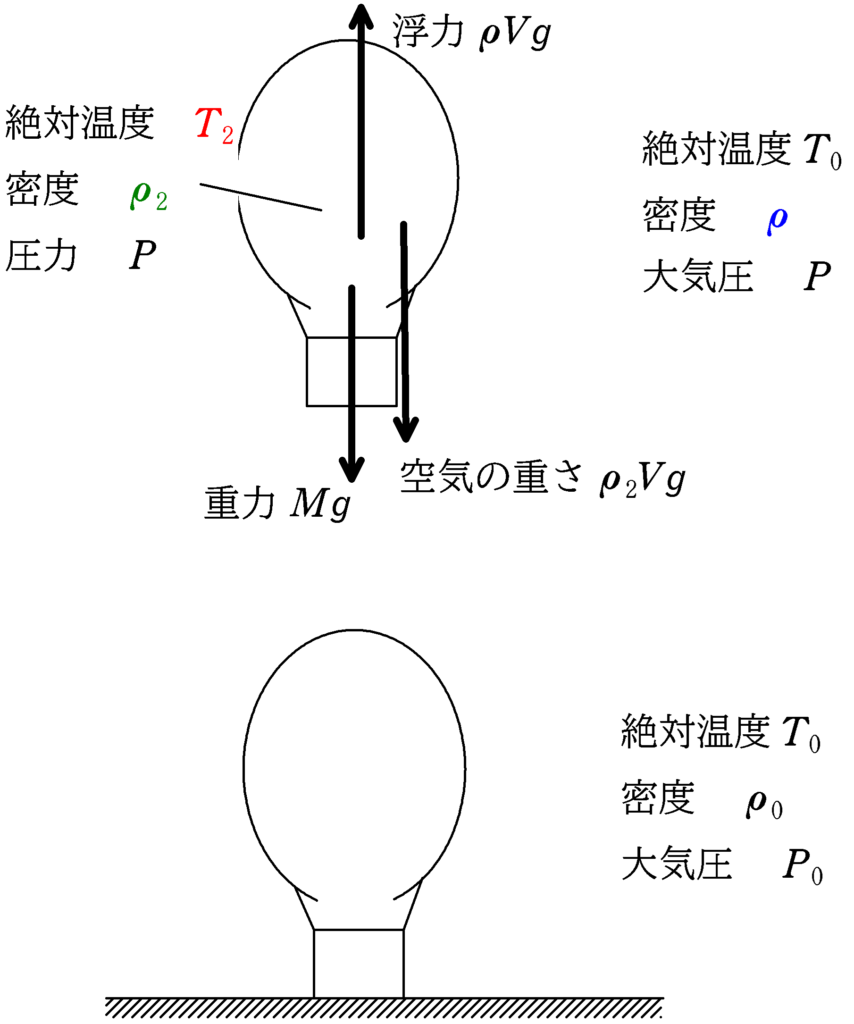
★ 気球のつり合いの式
$\rho Vg=Mg+\rho_{2}Vg$
$\therefore\,\,$$\rho$$V=M+$$\rho_{2}$$V$ $\cdots (\ast)$

さらに,$\dfrac{P}{\rho T}=一定$の式を立てます.

これは,どこで使えるんだろう??

$\dfrac{P}{\rho T}=一定$の式は分子量が同じであれば(今回はすべての場所で)使えます.
理由はこちらで確認してください.

じゃあ,今回は気球内外と地上と熱気球がある場所の大気それぞれに$\dfrac{P}{\rho T}=一定$の式を立てることができるね.
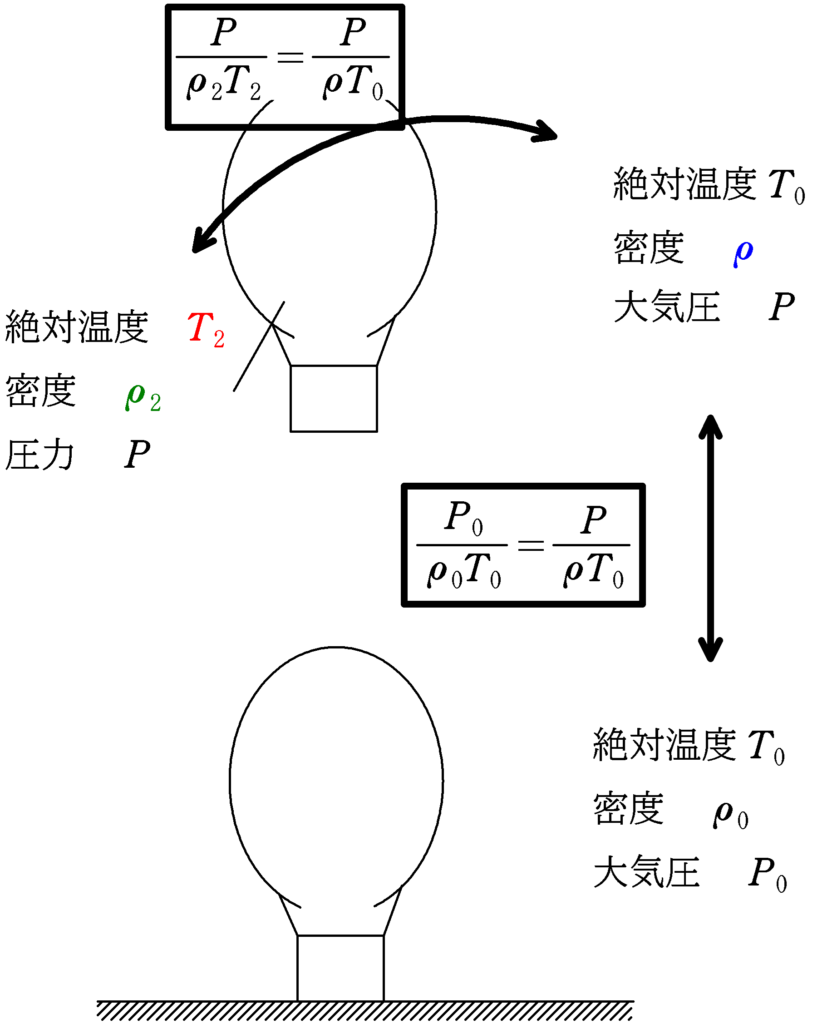
★ $\dfrac{P}{\rho T}=一定$の式
気球内外(気球内外の圧力は同じ!)
$\dfrac{P}{\rho_{2}T_{2}}=\dfrac{P}{\rho T_{0}}$
$\therefore\,\, $$\rho_{2}$$T_{2}$$=$$\rho$$T_{0}$ $\cdots (2\ast)$
地上と熱気球がある場所の大気
$\dfrac{P_{0}}{\rho_{0}T_{0}}=\dfrac{P}{\rho T_{0}}$
$\therefore\,\, $$\rho$$P_{0}=\rho_{0}P$ $\cdots (3\ast)$

あとは$(\ast)$,$(2\ast)$,$(3\ast)$を解けばよいです.実際はどの文字に消去して何を残せばいいのか迷うかもしれません.
今回は,$\rho$と$\rho_{2}$を消去して,$T_{2}$を求めます.
$\rho$$V=M+$$\rho_{2}$$V$ $\cdots (\ast)$
$\rho_{2}$$T_{2}$$=$$\rho$$T_{0}$ $\cdots (2\ast)$
$\rho$$P_{0}=\rho_{0}P$ $\cdots (3\ast)$
$(3\ast)$より,$\rho$$=\dfrac{\rho_{0}P}{P_{0}}$$\cdots (4\ast)$ を$(\ast)$に代入して
$\dfrac{\rho_{0}P}{P_{0}}\times V=M+$$\rho_{2}$$V$
$\therefore\,\, $$\rho_{2}$$=\dfrac{\rho_{0}PV-MP_{0}}{P_{0}V}$ $\cdots (5\ast)$
$(4\ast)$と$(5\ast)$を$(2\ast)$に代入して$T_{2}$を求めると
$\dfrac{\rho_{0}PV-MP_{0}}{P_{0}V}\times$$ T_{2}$$=\dfrac{\rho_{0}P}{P_{0}}\times T_{0}$
$\therefore\,\, $$T_{2}$$=\dfrac{\rho_{0}PVT_{0}}{\rho_{0}PV-MP_{0}}$ (答)

次回の内容はこちらです.




コメント